mat.analiz_1

називають стяжною системою вкладених відрізків, якщо:

а) [a1; b1] [a2 ; b2 ] ... [an ; bn ] ...,

б) довжина відрізків прямує до нуля при n → ∞ (рис.4.3).

a1 a2 a3 с b3 b2 b1 х

Теорема 4.2. Для довільної стяжної системи вкладених відрізків існує єдина точка, яка належить всім цим відрізкам.

Доведення. Оскільки послідовність відрізків (4.9) є вкладеною, то для кінців цих відрізків виконуються нерівності:

1)n N a1 ≤ a2 ≤.... ≤ an < bn ≤ ... ≤ b2 ≤ b1 ,

2)m, n N : am < bn (якщо m < n , то am ≤ an < bn ,

якщо m > n, то am < bm ≤ bn )

Розглянемо числову множину лівих кінців відрізків A ={an n N }. Вона обмежена зверху, оскільки an ≤ bm , тобто верхньою межею є правий кінець будь якого відрізка системи. Отже, множина А обмежена зверху і, згідно з принципом Вейєрштрасса, вона має точну верхню межу c = sup A.

Покажемо, що с належить всім відрізкам системи. Дійсно, оскільки с – верхня межа множини А, то n N an ≤ c , а оскільки с – найменша з усіх верхніх меж, то c ≤ bn . Тому c [an ; bn ], n N .

Покажемо тепер, що така точка с єдина. Припустимо, що існує ще

одна точка c0 ≠ c , яка	також належить усім відрізкам:
c0 [an ; bn ], n N і нехай c0 ≥ c. З того, що послідовність відрізків
стяжна, випливає, що ε > 0	n N : bn − an < ε .

Отже, ε > 0 n N :0 ≤ c0 −c ≤bn − an < ε , або 0 ≤ c0 −c < ε . Остання нерівність неправильна, оскільки достатньо взяти ε = 12 (c0 −c) і

матимемо:

50

0 ≤ c −c <	1	(c	0	−c)		:(c	0	−c)> 0 , або	0 ≤1 <	1	.
0	2								2

Отримали суперечність, яка і доводить, що точка c = sup A є єдиною точкою, яка належить всім відрізкам системи.

Приклад 3. [13, с.30] Довести, що для будь яких непорожніх обмежених зверху множин А і В:

sup(A B)= max{sup A; sup B}.

Розв’язання. Згідно з принципом Вейєрштрасса для кожної з множин А і В існує точна верхня межа:

a =sup A,		b =sup B, c = max{a; b}.
x A : x ≤ a,	x A B : x ≤ max{a; b }= c.
y B : y ≤ b,
Візьмемо довільне число ε		і, для означеності, будемо вважати, що

c = a . Тоді у множині А знайдеться число x': x'> a −ε = c −ε. Але це саме число x' A B. Таким чином, показано, що:

1)x A B : x ≤ c ;

2)ε > 0 x' A B : x'> c −ε .

Це означає, що c = sup(A B).

51

План:

1.Головний об’єкт аналізу, означення і способи задання функції.

2.Композиція і обертання функції.

3.Арифметичні операції над функціями.

4.Функція як інструмент для порівняння множин. Потужність множини.

Мета лекції: мати чітке уявлення про головний об’єкт математичного аналізу – функцію, знати арифметичні операції над функціями, а також композицію і обертання функцій.

Головний об’єкт аналізу, означення і способи задання функції.

Одним з основних понять математичного аналізу є поняття функціональної залежності. В багатьох явищах природи, техніки, економіки тощо можна вказати величини, які зв’язані між собою таким чином, що при зміні однієї величини змінюється і інша величина.

Розгляд реальних фізичних змінних величин приводить нас до висновку, що ці величини не завжди можуть приймати довільні значення. Так, швидкість матеріальної точки не може бути більша 3 1010 см/с (тобто швидкості світла в вакуумі), температура тіла не може бути меншою −2370 С, зміщення матеріальної точки, яка здійснює гармонійні коливання за законом y = Acos(ωt +δ ), може приймати значення тільки з відрізка [−A; A]. Абстрагуючись від конкретних фізичних властивостей змінних величин, які спостерігаються в природі, ми приходимо до поняття математичної змінної величини, яка характеризується тільки числовими значеннями, які вона може приймати.

52

Множина X всіх значень, які може приймати дана змінна величина x, називається областю зміни даної змінної величини.

Змінна величина вважається заданою, якщо задана область її зміни.

Надалі змінні величини будемо позначати малими буквами латинського алфавіту x, y, t,…, а області зміни цих змінних величин відповідно символами X, Y, Т,….

У функціональних залежностях обов’язково є принаймні дві змінні величини. Одні з них змінюються довільно, їх називають

незалежними змінними, або аргументами, інші змінюються залежно від перших, їх називають залежними змінними або функціями.

Приклади:

1. Нехай матеріальна точка рухається прямолінійно і рівномірно із сталою швидкістю v. Тоді шлях s, пройдений точкою за час t, обчислюється за формулою:

s =vt.

Звідси випливає, що шлях s залежить від часу t. Якщо t змінюється, то змінюватиметься і s, і чим більше часу точка рухається, тим буде довший шлях. Проте характер зміни величин t і s неоднаковий: t може набувати довільних додатних значень, тоді як зміна шляху s обумовлюється зміною t. Отже, t є незалежна змінна, а s – залежна змінна.

2.Нехай у провіднику протікає струм. Тоді, за законом Ома, залежність між силою струму I , електрорушійною силою Е і

опором провідника R виражається формулою: I = ER .

Якщо вважати, що опір провідника R є величина стала, то із зміною електрорушійної сили Е змінюється і сила струму I в провіднику. А саме, чим більша електрорушійна сила Е, тим більша і сила струму I . В останній формулі величина Е змінюється довільно, вона може набувати довільних додатних значень, тоді як величина I змінюється залежно від зміни Е.

53

Отже, тут Е – незалежна змінна, а I – залежна змінна.

3.Попит і пропозиція – дві основні категорії ринкових відносин, є взаємозалежними величинами. І та, і інша залежать від багатьох факторів, серед яких головний – ціна. Нехай q = d – попит на товар, p – ціна товару, S – пропозиція (від перших букв англійських слів

price – ціна, demand – попит, supply – пропозиція). Залежність між попитом і ціною називають функцією попиту q = f (p).

	Наприклад, q =	400	, або q = ae−2 p =	a	,	a = const .
		p +3		e2 p

4. Залежність між ціною і попитом можна розглядати як функцію

ціни від попиту p =ϕ(q). Наприклад, p = ln	5	.
	p
Сформулюємо означення функції.
Означення 5.1. Нехай маємо дві непорожні множини X і Y .

Якщо кожному елементу x X за певним законом поставлено у відповідність один елемент y з множини Y ( y Y ) , то кажуть, що на множині X визначено функцію y = f (x) ( f : X →Y ) із значеннями в множині Y .

При цьому множина X називається областю визначення або областю існування функції і позначається D( f ); а множина E(f )= {y Y y = f (x), x D(f )} Y – множиною значень функції або областю зміни функції f .

Змінну x називають незалежною змінною або аргументом,

y – залежною змінною або функцією, а f (x) називають значенням функції в точці x .

Отже, для того, щоб перевірити, чи є відповідність функціональна, потрібно перевірити, чи виконуються два ключових слова: „кожному” і „один”.

	КОЖНОМУ x X → ОДИН	y Y
	f
Слова функція, відображення, оператор – синоніми.
Приклади:

54

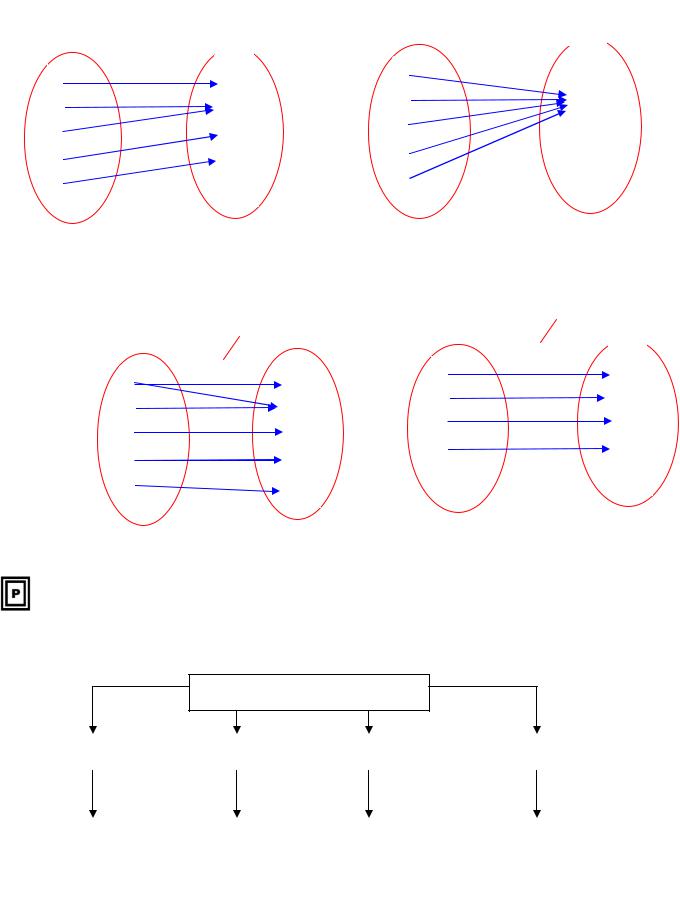
1) (Функціональна

залежність)

X

Y

f

•5	•А
•6	• В
• 7	• С
• 8	• D
• 9	• E

2) (Функціональна
залежність)	X	Y

f

• 5	•А
•6	• В
• 7	• С
• 8	• D
• 9	• E

X = D( f )		{A, B,C, D}= E(f )	X = D( f )
3) (Не функціональна			4) (Не функціональна
залежність)	X	Y	залежність)

f/

•	5	•	А		• 5
					•6
•6		• В
•	7	•		С	• 7
					8
• 8		• D			• 9
• 9		• E

{B}= E( f )

f Y

•А
•	В
•	С
• D

• E

не виконується умова – „один”

не виконується умова – „кожному”

Рис.5.1

Означення 5.2. Якщо множини X , Y є числовими, то функцію f (x) називають дійсною функцією дійсного аргументу.

Способи задання функції

Аналітичний	Табличний	Графічний	Словесний

Формулою

Таблицею

Графіком

Описом відповідності

Кожному працівникові

y = x2 +2

відповідає один оклад на

x

1

2

3

робочому місці

Рис.5.2

55

( ) 0, якщох ірраціональне число, y = D x :=

1, якщох раціональне число.

І. Аналітичний спосіб: задання функції за допомогою формули. Для цього використовують деякий запас вивчених і спеціально позначуваних формул, алгебраїчні дії і граничний перехід.

При цьому завжди під функцією, заданою формулою, розуміємо функцію, яка визначена на множині дійсних чисел, і для яких:

1)дана формула має зміст;

2)в процесі проведення всіх необхідних обчислень за цією формулою отримуємо тільки дійсні числа.

	y			Приклади функцій:
	2		5.	y = 4 − x2	. Ця функція задана
			на	відрізку	[−2;2]= D( y) ,	а
			множина її		значень – відрізок
			[0;2] = E ( f ).
−2	0	2	x 6. Функція		Діріхле,	яка
	Рис. 5.3		визначається			так:

D(y)= R, E(y)={0;1}.

Ця функція може бути задана або на множині дійсних чисел, або на
довільному відрізку		[a;b] R , а область її значень складається
лише з двох чисел 0 і 1.
1,	якщо	x > 0
	якщо	x = 0
7. y = sgn x := 0,
	якщо x < 0
−1,

(Термін sgn походить від латинського слова signum – знак). Читається „у дорівнює сігнум x”. Ця функція задана на всій числовій прямій(−∞;+∞), а множина її значень складається з трьох точок y = −1; y = 0; y = +1:

D(sgn )= R; E (sgn )={−1;0;1} (рис. 5.4).

56

Y				3	Y		y = x
1				2
				1			y = [x]
	X						X
0	-3	-2	-1	0	1	2	3
				-1
-1				-2
				-3
Рис. 5.4			Рис. 5.5

8. y = E(x) =[x], де символ [x] = E (x) означає цілу частину числа x , тобто найбільше ціле число, яке не перевищує x . Читається „у

дорівнює антьє x” (рис. 5.5).

9. Функцію можна задавати різними формулами на різних ділянках

−x,	x < 0,	(рис. 5.6).
своєї області існування. Наприклад, y =	x ≥ 0.
x2 ,

ІІ. Графічний спосіб.

Візьмемо прямокутну декартову систему координат.

Означення 5.3. Графіком функції y = f (x) ( x і y числа) називають множину точок з координатами (x; f (x)), x D( f ),

тобто Γf := {(x, y) x D(f ), y = f (x)}

				Y
	Y	M (x0	; f (x0 ))
y0
			X	X
0		x0		0
		Рис. 5.7		Рис. 5.6

Графічне зображення функції також може служити для задання функціональної залежності. Правда, це задання буде наближеним, тому що вимірювання відрізків практично можна проводити лише з

57

певним степенем точності. Прикладом графічного задання функції, які зустрічаються на практиці, є показання осцилографа.

Безпосередньо будувати графіки функцій по точках не завжди зручно, оскільки для кожної функції доводиться щоразу проводити значні обчислення. Тому зазвичай поступають інакше. Спочатку будують графіки деяких стандартних функцій, відомих вам з

шкільного	курсу	математики	(степеневих:	y = x2 , y = x3 , y =	k	;
показникової: y = ax , a > 0,					x
			a ≠1; тригонометричних: y = sin x ,
y = cos x ,	y = tg x,	y = ctg x ; логарифмічної:		y = loga x, a > 0, a ≠1

тощо), а графіки інших функцій намагаються отримати з уже відомих графіків за допомогою геометричних перетворень (паралельне перенесення, симетрія відносно точки або прямої, стиснення до осі, розтягування від осі).

Перетворення, які

Функція Графік необхідно провести з графіком y= f(x) на

площині XOY

	Паралельне перенесення
f (x) + a	вгору вздовж осі OY
	графіка функції f(x) на а
a ≠ 0	одиниць, якщо a > 0 , і
	вниз на	a	одиниць,
	якщо a < 0.

58

f (x − a) a ≠ 0

kf (x), k > 0, k ≠1

f (kx), k > 0,

k≠1

−f (x)

f (x)

Паралельне перенесення вправо вздовж осі ОХ на а одиниць, якщо a > 0 , вліво на a одиниць,

якщо a < 0.

Розтяг вздовж осі OY відносно ОХ в k разів, якщо k >1, стиск в 1/k разів, якщо 0<k<1.

Стиск вздовж осі ОХ відносно осі OY в k разів, якщо k >l, і розтяг в 1/k разів, якщо 0<k<1.

Симетричне відображення графіка відносно осі

ОХ.

Частина графіка, розташована нижче осі ОХ, симетрично відображається відносно цієї осі, решта частини графіка залишається без зміни.

59