mat.analiz_1

виконується, точки розриву поділяють на два роди.

Означення 14.3. Точка x0

називається точкою розриву першого

роду

функції

y = f (x),

якщо

існують

скінченні

односторонні

границі

lim f (x),

lim

f

(x) і при цьому:

x→x0 +0

x→x0 −0

10. lim f (x)

≠ f (x0 ),

x→x0 +0

або

(

)

(

0 )

x→x −0

f

x

≠ f

,

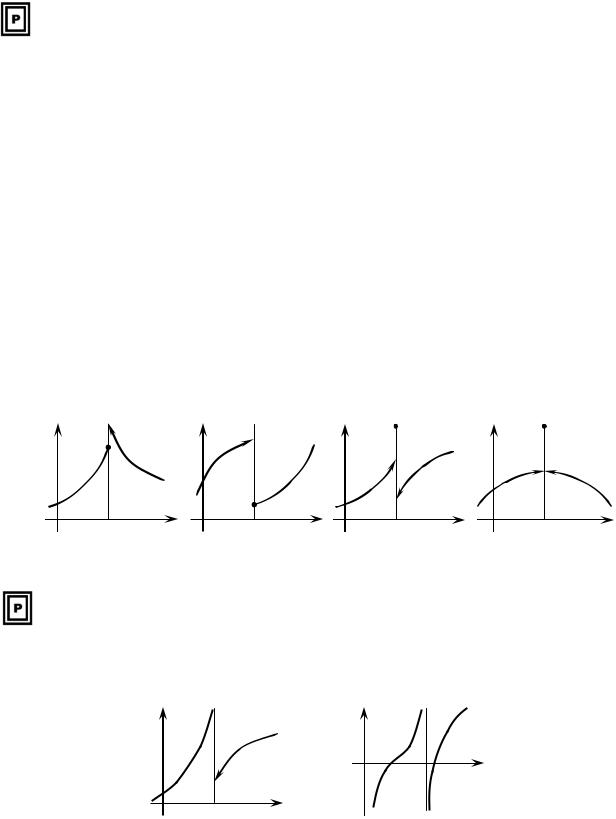
розрив І

роду(рис.14.2а)б)в));

20. lim

x

неусувний

0

або

30. lim

f (x)

≠ lim

f (x),

0

0

+0

x→x −0

x→x

або

– усувний розрив І роду (рис.14.2 г)).

40. lim

f

(

x

)

= lim

f

(

x

)

≠ f

(

x

x→x −0

x→x

+0

0 )

0

0

y

f (x)

y

y

f (x0 )

y

f (x0 )

f (x)

f (x)

f (x)

O

x0

x O

x0

x O

x0

x O

x0

x

а

б)

в)

г)

Рис. 14.2

Означення

14.4. Точка

розриву x0 функції

f (x)

називається

точкою розриву другого роду, якщо в цій точці не існує або дорівнює нескінченності принаймні одна з односторонніх границь

(рис.14.3 а) б)).

y			y
		y = f (x)			y = f (x)
			O	x0	x
O	x0	x		б)
	а		Рис. 14.3

170

Приклади. 1.

y =[x] (антьє від x ) (рис.14.4 ).

3

Y

1)

Нехай

x0 –

не ціле число, і [x0 ] = m ,

тобто

m < x0 < m +1

і

x [m;

m +1)

функція

2

1

y =[x] = m неперервна в усіх точках інтервалу

X

(m; m +1).

-3 -2 -1

0

1 2

3

-1

2)

x0 = m , тоді

lim [x] = m =[m] – функція

-2

неперервна

x→m+0

точці

m ;

-3

Рис. 14.4

справа

в

lim [x]

= m −1 ≠ m – маємо розрив зліва в точці

x→m−0

m. Значить точка m – точка неусувного розриву.

2. f (x)= x13 (x ≠ 0).

1) lim f (x)= lim

1

= −∞ – маємо розрив другого роду зліва.

x

x→0−0

x→0−0

2) lim f (x)= lim

1

= +∞ – маємо розрив другого роду справа.

x→0+0

x→0+0

x3

3.

f (x)= sin

1

; x0 = 0 .

x

1

lim sin

– не існує, отже маємо розрив другого роду.

x

x→0

4.

f (x)

=

sin x

– неперервна в усіх точках, крім x = 0 . Оскільки існує

x

0

lim sin x =1, то маємо розрив першого роду усувний. Якщо розглянути

x→0 x

функцію

		sin x				, x ≠ 0,
							,
				x
	F (x) =
				1,		x = 0,
то вона є неперервною на R .
Розрив функції	f (x)	називають усувним						тому, що можна так
довизначити функцію	f (x) в точці x0 , що „довизначена” функція F (x)
стає неперервною	в	точці			x0 . Для			цього покладемо:

171

	(	x		)		0
f					, якщо x ≠ x
F (x)=			f (x),			якщ о x = x0
limx→x
	0
Означення 14.5. Якщо x0 – точка розриву першого роду функції
f (x)	і якщо права границя функції f (x)							в точці x0 не дорівнює
лівій границі цієї функції в цій точці,							то модуль різниці правої і
лівої гран иць						фун кції f (x) в точці	x0	називають стрибком

фун кції в точ ці :

			li m f (x)− lim f		(x)	.
			x→x0 +0	x→x0 −0
Г раниця і точк и розриву монотонної функції.
Існування границі функції				f (x)	в точці x0 досить просто
вирішується для монотонних функцій.
Теорема 14.1.		Нехай функція		f (x)	монотонно зростає на
множині Х і	x0	– гранична точка цієї множини (скінченна або
нескінченна).	Як що f (x) обмеж ена зверху, то в точці x0 вона
має скінченну границю. В протилежному випадку lim							f (x)= +∞ .
						x→x0
Доведення:
І. Нехай функція	f ( x) обмежена зверху на множині Х,						отже існує

sup { f (x)} = A . Покажемо, що число А буде границею функції f (x)

x X ,x<x0

в точці x0 .

A = sup{f (x)} = A 1) x X : f (x)≤ A,

x X

2) ε > 0 x1 < x0 : f (x1 )> A −ε.

2) 1)

Отже, x X : x1 < x f (x1 )< f (x) A −ε < f (x1 )< f (x)≤ A < A +ε ,

тобто ми показали, що у випадку скінченної точки x0 :

172

ε > 0 δ = x0	− x1	> 0, x Oδ* (x0 )∩ X		f (x)− A		<ε lim f (x)= A, а
						x→x0
у випадку x0 = +∞ :

ε > 0 x1 X , x X : x > x1			f (x)− A		<ε lim f (x)= A.
					x→+∞

ІІ. Нехай функція	f (x) необмежена зверху на множині Х при x → x0 ,
це означає, що
M > 0 x X ∩O* (x		): f (x )> M x X ∩O*	(x	): x > x
1	0	1	0	1
	f (x)> f (x1 )> M .
Отже, функція f (x) є нескінченно великою в точці x0			і	lim f (x)= +∞
			x→x0

. ■

Теорема 14.2. Неспадна (незростаюча) функція f (x) може мати на множині X розриви тільки першого роду, тобто стрибки.

Доведення.

Візьмемо довільну точку x0 X , яка не є лівим кінцем цього

проміжку. Для x ≤ x0 застосуємо теорему 14.1 про границю монотонної
функції:				)	якщо				f (x)≤ f (x0 ),	то існує скінченна границя
x→x −0	f	(	x		≤	f	(	0 )	.
lim								x
0
	Якщо ліва границя дорівнює									f (x0 ), то функція f (x) неперервна в
точці x0				зліва;				якщо ж границя не дорівнює f (x0 ), то маємо стрибок.

Аналогічно, якщо взяти точку x0 X , яка не є правим кінцем, то в точці x0 буде f (x) або неперервна справа, або стрибок.

З допомогою доведеної теореми можна встановити критерій неперервності монотонної функції, зручний на практиці.

Теорема 14.3. Якщо значення монотонно зростаючої (спадної) в проміжку X функції f (x) міститься у проміжку Y і суцільно

173

заповнюють його (так, що кожне значення y з Y функція приймає принаймні один раз), то ця функція неперервна на X .

Доведення проведемо методом від супротивного. Нехай в деякій точці x0 X монотонна функція f (x) має, наприклад, розрив зліва. За теоремою 14.2 це може бути тільки стрибок:

x→x −0

f

(

x

)

≤

f

(

0 )

.

lim

x

(

)

0

(

)

(

)

(

0 )

0

f

x

x→x −0

x

,

а для

0

x

≥ f

x

, то

Отже, для x < x

≤ lim f

x > x f

0

y ,

функція

не

може

приймати значень

які

лежать

між

числами

x→x −0

(

x

)

і

f

(

0 )

,

і

належать

проміжку

Y .

Це суперечить

умові

lim f

x

0

теореми, значить, функція f (x) розривів не має.

Показниковa функція та її основні властивості.

Означимо тепер степінь для довільного дійсного числа x .

Означення 14.6. Нехай a > 0 , а x – довільне дійсне число. Нехай {rn }– послідовність раціональних чисел, збіжна до x ( x R така послідовність завжди існує). Степенем числа а з дійсним показником х називається границя:

. (14.1)

Це означення коректне в тому смислі, що вказана границя завжди існує і не залежить від вибору послідовності {rn }, збіжної до числа x R

. Доведення можна прочитати в [ 8, с.206]

Означення 14.6 природне в тому смислі, що у випадку, коли x є раціональним числом r , то степінь ax співпадає з ar у відомому раніше розумінні. Дійсно, якщо x = r – раціональне число, то за послідовність {rn }, збіжну до r , можна взяти (rn )= (r ). Тоді, згідно з означенням маємо:

ax := lim arn = lim ar = ar .

n→∞ n→∞

Означення 14.7. Нехай задано деяке число a > 0 . Функція y = ax ,

174

визначена x R , називається показниковою функцією.

Згідно з	означенням: 1x =1 x R .	Тому	випадок a =1 є
тривіальним, і надалі ми не будемо його розглядати.
Теорема	14.4. Показникова функція	ax	(a > 0) має такі

властивості:

1)При a >1 вона строго зростає, а при 0 < a <1 – строго спадає на всій числовій осі;

2) ax1 ax2 = ax1 +x2 , x , x	2	R ;
1

3) (ax1 )x2 = ax1x2 x1, x2 R ;

4)Вона неперервна в кожній точці числової осі;

5)E (ax )= R+ .

Доведення.

y = ax		Y
		y = ax
(0 < a <1)		(a >1)
	1
		X
	0	Рис. 14.5

1. Розглянемо випадок a >1. Нехай x1 < x2 .

Доведемо, що	ax1 < ax2 .
неперервності	множини

існують раціональні числа місце нерівність

За властивістю

дійсних чисел r′ і r′′, що має

x1 < r′ < r′′ < x2 .

Виберемо довільно послідовності раціональних чисел {rn′} і {rn′′} такі, що

lim r′ =	x ,	lim r′′=		x	і r′ < r′	< r′′ < r′′	n =1, 2... Тоді arn′		< ar′ < ar′′ < arn′′
n→∞ n	1	n→∞	n	2	n	n	ax1 ≤ ar′ < ar′′ ≤ ax2
, перейдемо до границі при n → ∞:									ax1	< ax1 при
x1 < x1 .
Випадок 0 < a <1 розглядається аналогічно.
2. Доведемо другу властивість ax1 ax2 = ax1+x2 .
Нехай числові послідовності {rn′}							і {rn′′}	такі, що lim rn′ = x1 ;		lim rn′′= x2
		′	′′					n→∞		n→∞
, отже						Тоді, згідно		з означенням показникової
	lim(rn		+ rn )= x1 + x2 .
	n→∞

функції маємо:

175

x +x

r ′+r ′′

=

lim

(

r ′

r

′′

)

=

r

′

r ′′

x

x

a 1

2 = lim a n

n

a n

a n

lim a n

lim a n

= a 1

a

2 .

n→∞

n→∞

n→∞

n→∞

З властивості 2) випливає ax a−x

= a0 =1

.

3. Доведемо властивість:

(ax1 )x2 = ax1x2 .

1) Нехай спочатку x2

= p – натуральне число, то з властивості 2) маємо

(ax )p

р

разiв

= ax ax ... ax = ax+x+...+x

= a px .

р

разiв

2) Якщо x2 =

1

, де q

– натуральне число (q >1), то

q

x1 q

q

разiв

x1

x1

x1

x1

x1

x1

x1

a

+

+...+

= a

q = ax1 ,

q

= a

q

a

q

... a

q

= a

q

q

q

q

q

разiв

тобто

x1

q

= ax1

,

а

за

означенням

кореня

q го

степеня

маємо:

a q

1

x1

(ax1 )q

= a

.

q

p

1

1

px

p

x

x

p

q

px

1

x x

q

3) Якщо

x2

=

,

то

(a

1 )q

= (a 1 )

= (a

1 )q = a

= a

1 2 ,

тобто

q

r =

p

Q

: (ax1 )r = ax1r .

q

4) Розглянемо загальний випадок, коли x2 –

дійсне число. Візьмемо

довільну послідовність {rn } раціональних чисел, збіжну до x2

(rn n→→∞ x2 ).

Тоді n N :

(ax1 )rn

= ax1rn

(14.2) і

lim ax1rn

= ax1x2 .

n→∞

176

З іншого боку, враховуючи означення показникової функції, отримаємо

lim (ax1 )rn = (ax1 )x2 . n→∞

Використовуючи останні дві рівності, і переходячи в (14.2) до границі,

остаточно отримаємо: (ax1 )x2 = ax1x2 .

4. Доведемо, що функція ax неперервна в кожній точці числової осі. Використовуємо четверте означення неперервної функції в точці, для цього обчислимо приріст функції:

y = f (x0 + x)− f (x0 )= ax0 +Δx − ax0 = ax0 (a x −1).

		1	1		1
	а) Нехай a >1. Тоді lim n a = liman		=1 і lim a−n	= lim		=1, тобто
					1
	n→∞	n→∞	n→∞	n→∞ an
			1	1
	ε > 0 n , n > n : 1−ε < a−n			< an <1+ε .
	0	0

Оскільки x →0 , то завжди можна вибрати таке натуральне число n , що − 1n < x < 1n , отже

1

1

1

1

a−n < a x < an

1 −ε < a−n < a x < an <1 +ε , то

a x −1

< ε ,

тобто lim a x =1.

x

→0

б) Нехай 0 < a <1, покладемо a =

1

(b >1)

дістанемо

b

lim а x

= lim

1

x

=

lim

1

=1.

x

x→0

x→0

b

x→0 b

Тоді lim

y = lim a

x0

(

a

x

−1

= a

x0

lim

a

x

−1

= a

x0

(1 −1)= 0 .

x→0

x→0

)

x→0 (

)

5. Доведемо, що E (ax )= R+ .

Використаємо той факт, що ax ,

a > 0,

a ≠1 є неперервною і строго

монотонною функцією. Зокрема, при a >1 функція y = ax є

177

неперервною і зростає, тому згідно з теоремою про границю монотонної функції, достатньо довести, що

	lim ax = +∞, lim ax = 0 ,
	x→+∞				x→−∞
оскільки ці границі існують.
lim ax = +∞	df (Гейне)			): lim x = +∞
		(x
x→+∞			n		n→∞ n
lim ax = 0	df (Гейне)		x ′	)	: lim x ′ = −∞
x→−∞			( n		n→∞ n

В першому випадку візьмемо (xn )= (n):

a >1 a =1+α, α > 0,

lim axn = +∞,

n→∞

lim axn′ = 0,

n→∞

an = (1+α)n =1+ nα +

n(n −1)

α2 +... +αn >1 + nα → + ∞,

2!

n→∞

отже, lim an = +∞.

n→∞

В другому випадку візьмемо

(

x ′

= (−n), отже lim a−n

= lim

1

= 0.

n )

n→∞

n→∞ an

Аналогічно доводиться

випадок для

0 < a <1.

Покладемо

b =

1

, b >1, маємо: lim ax = lim

1

= 0;

lim ax = lim

1

= +∞ .

a

x→+∞

x→+∞ bx

x→−∞

x→−∞ bx

Графік показникової функції зображено на рисунку 14.5.

178

План:

1.Обмеженість неперервної на відрізку функції.

2.Найбільше і найменше значеннянеперервної на відрізку функції.

3.Теореми про проміжне значення функції.

Мета лекції: знати основні властивості функцій, неперервних на відрізку.

Обмеженість неперервної на відрізку функції.

Означення 15.1. Функція y = f (x) називається неперервною на відрізку [a;b], якщо вона неперервна в інтервалі (a;b), неперервна справа в точці x = a і неперервна зліва в точці x = b.

Функції, які неперервні на відрізку [a;b], мають властивості, яких, взагалі кажучи, не мають функції, неперервні, наприклад, в інтервалі. Ці

властивості ми і розглянемо сьогодні.

Теорема 15.1 (перша теорема Вейєрштрасса). Якщо функція

y = f (x) неперервна на відрізку					[a; b], то вона на ньому
обмежена.
Доведення проведемо методом від супротивного. Припустимо, що
функція	f (x) неперервна на відрізку [a;b], але необмежена на ньому.
Тоді n	(xn ) [a;b], n N така, що
		f (xn )		> n .	(15.1)

Послідовність {xn } – обмежена. За теоремою Больцано Вейєрштрасса з цієї послідовності можна виділити збіжну підпослідовність

179