mat.analiz_1

Теорема 27.1 (достатня умова строгої опуклості). Нехай функція f (x) двічі диференційовна на інтервалі (a, b). Тоді,

якщо f ′′(x)< 0 на (a, b), то функція f (x) строго опукла вгору

(опукла), а якщо f ′′(x)> 0 на (a, b), то функція f (x) строго

опукла вниз (вгнута) на цьому інтервалі.

Доведення. Візьмемо довільні точки x1, x, x2 : a < x1 < x < x2 < b. Тоді

l (x)− f (x)=		f (x2 )(x − x1 )+ f (x1 )(x2 − x)		− f (x)		x2 − x1 +(x − x)				=
		x	− x
						x	− x
		2	1		2		1
=	f (x2 )(x − x1 )+ f (x1 )(x2 − x)− f (x)(x − x1 )− f				(x)(x2 − x)				=
			x2 − x1
=	( f (x2 )− f (x))(x − x1 )+( f (x1 )− f (x))(x2 − x)				.
		x2 − x1

Застосувавши до виразів в правій частині останньої рівності теорему Лагранжа, одержимо

l (x)

− f (x)=

f ′(c )(x − x)(x − x )− f ′(c )(x − x

)(x − x)

=

1

2

1

2

1

2

( f

′(c1 )− f ′(c2 ))(x2

x2 − x1

=

− x)(x − x1 )

;

x

< c < x < c

< x

x2 − x1

1

2

1

2

c2

c3 c1

До різниці

f ′(c )− f

′(c )

застосуємо

b

а x1

x

x2

1

2

ще раз теорему Лагранжа, отримаємо

l (x)− f (x)=

f ′′(c3 )(c1 −c2 )(x2 − x)(x − x1 )

,

причому

c −c > 0,

x2 − x1

1

2

sgn (l (x)− f (x))= sgn f ′′(c3 ).

x2 − x > 0,

x − x1 > 0, тому

f ′′(x)< 0 x (a, b)

l (x)− f (x)< 0 l (x)< f (x)

функція

f (x) - строго опукла вгору на (а, b);

f ′′(x)> 0 x (a, b)

l (x)− f (x)> 0 l (x)> f (x)

функція

f (x) - строго опукла вниз на (а, b)

■.

290

Зауважимо, що умови знакосталості другої похідної для опуклості функції є достатніми, але не необхідними. Так, наприклад,

функція y = x4	строго опукла вниз на всій числовій прямій, однак її
Y	друга похідна y′′ =12x2	перетворюється в нуль при
	x = 0 (рис.27.3).
	Приклад 1. Знайти інтервали вгнутості й
	опуклості кривої y = 3x4 −8x3 + 6x2 +12 .
0	X Розв’язання.
Рис 27.3	y′ =12x3 − 24x2 +12x,	y′′ = 36x2 − 48x +12,

y′′ = 0 3x2

+ -

1

3

Крива y (x)

− 4x +1 = 0, D =16 −12 = 4; x

=

4 − 2

=

1

; x

=1.

1

6

3

2

+

′′

знак f (x)

1

Поведінка

f (x)

1

опукла вгору на проміжку

; 1

,

вгнута вниз на

3

проміжках −∞ ;

1

і (1

; +∞).

3

Отже з теореми 27.2 ми робимо висновок, що опуклість догори

чи

донизу

функції

f (x)

залежить від знаку другої похідної. Але

опуклість функції можна також зв’язати з дотичною до графіка.

Теорема 27.2. Нехай функція

f (x)

має на всьому інтервалі (а, b)

у

f (x)

додатну

(від’ємну)

другу

похідну:

L(x)

f ′′(x)> 0 ( f ′′(x)< 0).

Тоді, для довільної

f (x0 )

точки

x

(a,b)

і x (a,b),

x ≠ x

всі

0

0

точки

(x, f (x))

графіка функції

f (x)

лежать

вище

(нижче)

дотичної,

0

а

х

х

0 х

b

x

проведеної до нього в точці (x0 ,

f (x0 )).

Рис.27.4

Доведення.

Запишемо

рівняння

291

дотичної	до	графіка		функції	f (x)	в	точці	x0
L(x): y = f ′(x		)(x − x	)+ f (x	).
	0	0	0

Оцінимо різницю (використовуючи теорему Лагранжа)

f (x)− L(x)= f (x)

− f (x )− f ′(x )(x − x )=

0

0

0

= f ′(c1 )(x − x0 )− f ′(x0 )(x − x0 )=

= ( f ′(c1 )− f ′(x0 ))(x − x0 )= f ′′(c2 )(c1 − x0 )(x − x0 )

f (x)− L(x)= f ′′(c

)(c − x

)(x − x )

2

1

0

0

Точка c1 лежить між x і x0 , а точка c2

- між c1 і x0

(рис.27.5).

або

x

c1 c2

x0

x0

c2

c1

x

Рис.27.5

Оскільки (c1 − x0 )(x − x0 )> 0,

то sgn( f (x)− L(x))= sgn( f ′′

(c2 )) (27.5)

f ′′(x)> 0

x (a,

b)( f (x)

вгнута)

f (x)− L(x)> 0

f (x)> L(x),

f ′′(x)< 0

x (a,

b)( f (x)

опукла)

f (x)− L(x)< 0

f (x)< L(x).

■

ІІ спосіб доведення теореми.

Доведення можна провести, використовуючи формулу Тейлора, оскільки функція f (x) двічі диференційовна на (a ; b).

f (x)= f (x0 )+ f ′(x0 )(x − x0 )+

f ′′(x

)

(x − x0 )

2

+ o((x − x0 )

2

), x → x0 ,

0

2!

f (x)− L(x)= f (x0 )+ f ′(x0 )(x − x0 )+

f ′′(x0 )

(x − x0 )2 + o((x − x0 )2 )−

2!

− f (x0 )− f ′(x0 )(x − x0 )=

f ′′(x0 )

(x − x0 )2 + o((x − x0 )2 ).

2

а o((x − x0 )2 )

Тут (x − x0 )2 > 0 x O* (x0 ),

-

нескінченно

мала

функція вищого порядку малості,

ніж (x − x

)2

при x → x ,

тому

0

0

sgn( f (x)− L(x))= sgn( f ′′(x0 ))

.■

292

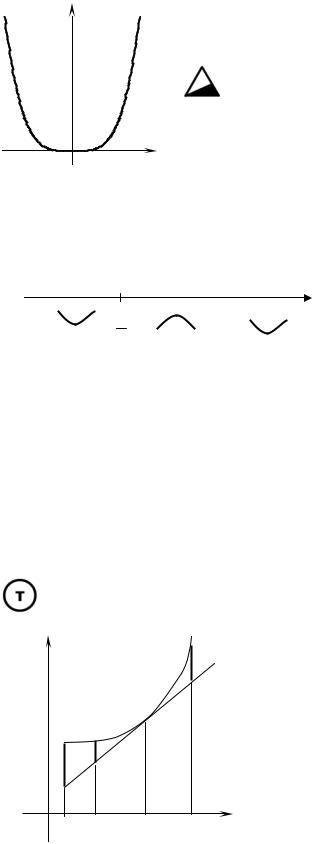
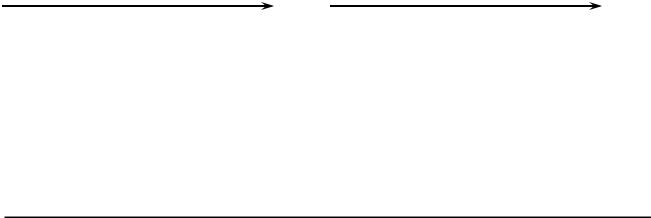
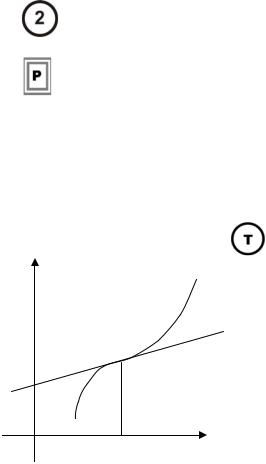
Точки перегину. Необхідні і достатні умови.

Означення 27.3.

Нехай функція диференційовна в точці x = x0

і

нехай

L(x)= 0 – рівняння дотичної до графіка функції

f (x)

в

точці

(x0 , f (x0 )). Якщо різниця f (x)− L(x)

замінює знак при

переході через точку x0 , то x0 називається точкою перегину

функції f (x) (рис. 27.6).

Теорема 27.4 (необхідна умова перегину).

f (x)

Якщо в точці перегину існує друга

L(x)

похідна, то вона дорівнює нулю.

Доведення . Нехай x - точка перегину і в

0

f ′′(x),

і

-

цій точці існує

друга

похідна

нехай y = L(x),

де

0

х0

х

L(x)≡ f (x )+ f '(x )(x − x ) –

0

0

0

Рис.27.6

дотична до графіка в точці

x0 .

Тоді за

формулою Тейлора маємо:

f (x)− L(x)=

f ′′(x0 )

(x − x0 )2 + o((x − x0 )2 ),

x → x0 , і

2

!

sgn( f (x)− L(x))= sgn( f ′′(x0 )). Якби f ′′(x0 )≠ 0 , то f (x)− L(x)>< 0 в

деякому O(x0 ). Отже, різниця f (x)− L(x) не змінювала б знак в точці x0 і точка x0 не була б точкою перегину, що суперечить умові. Тому f ′′(x0 )= 0 .

Теорема 27.5 (достатня умова точки перегину). Якщо функція f (x) диференційовна в точці x0 , двічі диференційовна в деякому

Oδ* (x0 ) і друга похідна f ′′(x) змінює знак при переході аргумента через x0 , то x0 є точкою перегину функції f (x).

Доведення. Функція f (x) задовольняє умови теореми 27.3, отже, виконується умова (27.5), точка c2 лежить між c1 і x0 , тобто по ту ж

293

сторону

від

x0 ,

що

і

точка

х

(рис.

27.5)

в

рівності

f (x)− L(x)= f ′′(c2 )(c1 − x0 )(x − x0 ). Отже,

якщо

f ′′(x)

змінює знак

при переході аргумента через точку x0 , то різниця

f (x)− L(x) також

змінює знак і точка x0

є точкою перегину функції

f (x).■

Приклад 2.

Знайти інтервали опуклості і точки перегину функції

y =

x

.

1

+ x2

D(y)= R;

Розв’язання: 1.

знак f ′

1

+ x2 − 2x2

1 − x2

–

+

–

+

2. y′ =

=

;

−

3

0

+ 3

поведінка f

(

2

)

2

(

+ x

2

)

2

1 + x

1

т.перегину

т.перегину

т.перегину

2x(x2

−3)

3. y′′

x = 0,

Рис.27.7

=

;

y′′ = 0

(

)

3

2

x = ± 3

1+ x

Відповідь. Крива опукла на проміжках (−∞ ; − 3 )

і (0 ;

3 ), вгнута

на (− 3 ; 0) і (

3 ; + ∞), точки x = 0 і x = ±

3 є точками перегину.

Нерівність Ієнсена.

f (x) –

Теорема 27.6 (нерівність Ієнсена). Нехай

опукла вниз

(вгнута)

на

(a,b)

функція.

Тоді n ≥ 2

і {x1, x2 ,..., xn } (a,b) і

{α1,α2 ,...,αn } (0,1):α1 +α2 +... +αn

=1

f (α1x1 +α2 x2 +... +αn xn )

≤

α1 f (x1 )+α2 f (x2 )+... +αn f (xn )

(27.6)

Доведення. При n = 2 нерівність (27.6) збігається з нерівністю (27.2) означення опуклої вниз функції. Припустимо, що (27.6) правильна для m = n −1, і покажемо, що нерівність (27.6) правильна для m = n.

Нехай в наборі α1,α2 ,...,αn число α1 ≠ 0. Тоді позначимо

294

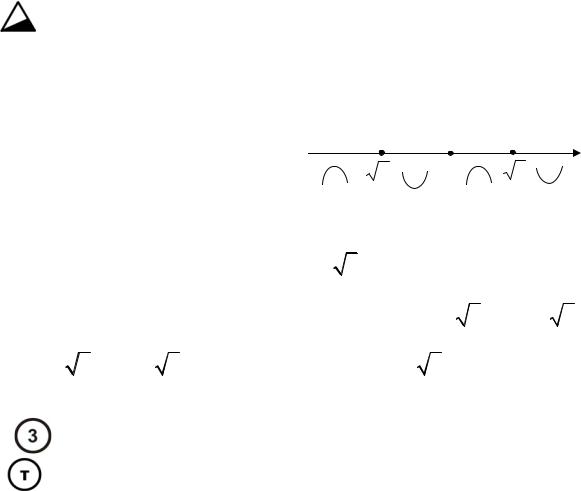
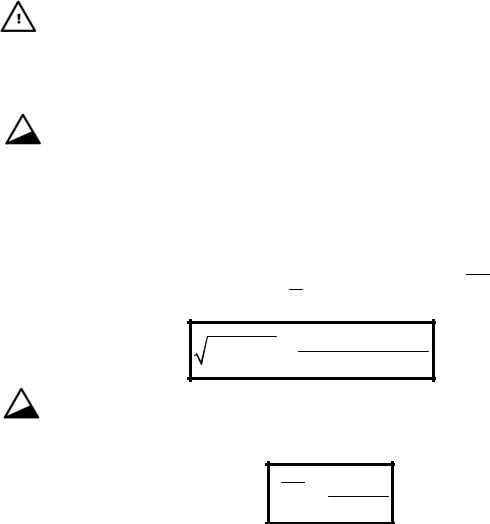
β =α

2

+α

3

+... +α

n

> 0 α2

+

α3 +... + αn =1,

α + β =1

i

β

β

β

1

f (α1x1 +α2 x2 +... +αn xn )= f

α

α

(За означенням

27.2)

α1x1 + β

2

x2 +... +

n

xn

≤

β

β

f

(x

)+ β f

α

x

+...

α

x

(За припущенням для m=n−1)

≤α

2

+

n

≤

1

1

β

2

β

n

≤α

1

f

(x

)+ β

α2 f (x

)+... + αn f (x

)

=α f (x

)+α

2

f (x

)+... +α

n

f (x

)

1

β

2

β

n

1

1

2

n

оскільки

точка

α2

x +...

+ αn

x

(a,b),

що

й

потрібно

було

β

2

β

n

довести.■

Якщо функція f (x)

строго опукла вниз на (a,b), тоді нерівність

(27.6) також строга.

f (x)

– опукла вгору (опукла) на (a,b),

Зауваження. Якщо функція

тоді

f (α1x1 +α2 x2 +... +αn xn )≥α1 f (x1 )+α2 f (x2 )+... +αn f (xn )

(27.7)

Приклад 3.

Функція y = ln x строго опукла вгору на (0, +∞), тому

ln (α1x1 +α2 x2 +... +αn xn )>α1 ln (x1 )+α2 ln (x2 )+... +αn ln (xn ),

або

ln (α

x +α

2

x

+... +α

x

)

> ln xα1

xα2

... xαn ,

1

1

2

n

n

1

2

n

або

xα1 xα2 ... xαn

<α x +α

2

x +... +α

n

x .

1

2

n

1

1

2

n

Покладемо α1 =α2

=... =αn

= 1 , тоді xi

≥ 0 (i =1, n):

n

n x1 x2 ...xn

≤ x1 + x2 +... + xn .

n

Приклад

4.

Функція

y = ex

опукла

вниз

(вгнута)

на

R ,

тому

{x, y} R

i

{α, β} (0;1):α + β +1 eαx+β y

≤α ex + β ey .

x+y

x

y

Покладемо α = β =

1

, тоді e 2

≤ e

+ e

.

2

2

295

План:

1.Похилі і вертикальні асимптоти.

2.Загальна схема дослідження функції.

3.Побудова графіків функцій, заданих формулою y = f (x).

Похилі і вертикальні асимптоти.

Означення 28.1. Нехай функція					f (x) визначена x > a (x < a).
Якщо	існують			такі	числа	k і	l ,	що
lim	f (x)−(kx +l )	)	= 0	(x → −∞),	то	пряма	y = kx +l
x→+∞(
називається похилою асимптотою графіка						функції	f (x)	при

x → +∞(x → −∞).

Існування асимптоти графіка означає, що при x → +∞(x → −∞) функція веде себе «майже як лінійна функція», тобто відрізняється

	від лінійної функції на нескінченно малу величину.
	y						Вияснимо геометричний				зміст
							похилої	асимптоти.		Нехай
						B	M (x, f (x))– точка графіка функції
		y = f (x) М			θ		f (x),	M0 (x,0)	- проекція		цієї
		θ	Q		Р		точки	на	вісь		Ox ,
	0		M 0			x	АВ - асимптота,		θ -	кут	між
		y = kx +l
	A						асимптотою і додатним напрямом
		Рис.28.1
							осі Ox ,	MP AB,	кут θ ≠	π .
										2
	MM0 = f (x), QM0 = kx +l;					MQ = MM0 −QM0 = f (x)−(kx +l ).
							296

З

прямокутного

трикутника

MPQ

( MPQ = 900 , PMQ =θ )

маємо:

MP = MQ cosθ.

Оскільки

cosθ

<1,

то

MP

і

MQ

відрізняються

дуже

мало,

тому

при

x → +∞:

lim MQ = 0

lim MP = 0 .

Завдання полягає в тому, щоб знайти

x→+ ∞

x→+ ∞

коефіцієнти k і l асимптоти.

функції f (x)

Нехай

y = kx +l

похила

асимптота

графіка

приx → +∞,

тобто f (x)= kx +l +α (x),

де lim α (x)= 0 . Поділимо

x→+ ∞

останню рівність на x:

f (x)

=

kx

+

l

+

α (x)

і перейдемо до границі

x

x

x

x

f

(

x

)

l

α

(

x

)

при x → + ∞:

lim

= lim

k

+

+

= k

;

x

x

x→+ ∞

x→+ ∞

x

lim

(

f (x)− kx

)

= lim

(

l +α

(x)

)

= l.

x→+ ∞

x→+ ∞

Аналогічно

знаходимо

кутовий

коефіцієнт

і

вільний член

при

x → − ∞:

k =

lim

f

(x)

,

l =

lim

(

f

(x)− kx

)

(28.1)

x→+ ∞

x

x→+ ∞

( x→− ∞)

( x→− ∞)

Правильне і обернене

твердження:

якщо

числа

k

і l

задовольняють умову (28.1), то пряма y = kx +l

є асимптотою графіка

функції

f (x). Дійсно:

lim

f (x)− kx

)

= l f (x)− kx −l =α (x) -

x→+∞ (

( x→−∞)

нескінченно

мала

функція

при

x → +∞ (x → −∞)

lim

(

f

(

x

)

− kx −l

)

= 0, отже, згідно

з означенням 28.1,

пряма

x→+∞

(x→−∞)

y = kx +l

є

похилою

асимптотою графіка

функції

f (x)

при

x → +∞ (x → −∞).

Означення

28.2.

Нехай

функція

f (x)

визначена

в деякому

O* (x

)

і

нехай

виконується

принаймні одна

з

умов:

0

297

y

0

lim = +∞(−∞)

або lim

= +∞(−∞).

Тоді

пряма

x = x0

x→x0 −0

x→x0 +0

називається вертикальною асимптотою графіка функції

f (x)

(рис.28.2).

В цьому випадку відстань MP =

x − x0

між

М

Р

точкою

M (x, f (x))

графіка функції і

f (x)

прямою x = x0 прямує до нуля, якщо точка М

вздовж графіка функції прямує в

х

х0 х

нескінченність.

Рис.28.2

Приклад 1. Знайти похилі і вертикальні

асимптоти графіка функції

f (x)=

2x2 + x

.

x +1

Розв’язання.

Знайдемо похилі асимптоти:

1

k = lim

f (x)

= lim

2x2 + x

= lim

2 + x

= 2;

x

1

x→±∞

x→±∞ x2 + x

x→±∞

1 + x

l = lim( f (x)− kx)=

2x2 + x

−x

lim

− 2x = lim

= −1.

x +1

x→±∞

x→±∞

x→±∞ x +1

Отже, пряма y = 2x −1 є похила асимптота на +∞ і −∞.

Вертикальні асимптоти: x = −1, оскільки lim f (x)

= lim

2x2 + x

= ∞.

x→−1

x→−1

x +1

Зауваження.

Якщо функція є раціональною f (x) =

P(x)

, то

Q(x)

вертикальними

асимптотами

будуть

прямі

x = x0 : Q(x0 )= 0, P(x0 )≠ 0.

Загальна схема дослідження функції і побудова її графіка.

Графік заданої функції можна будувати за довільно взятими точками. Однак при такому способі можна і не виявити всіх особливостей її графіка. Загальна схема дослідження функції включає

298

такі елементи, як зростання і спадання, точки екстремуму, проміжки опуклості тощо. Цим самим ми знаходимо характерні точки для даного графіка і тим спрощуємо свою роботу над побудовою графіка.

При дослідженні функції і побудові графіка варто дотримуватись такої схеми:

Перший етап (використання вигляду заданої функції).

1.Знайти область визначення функції, область неперервності і точки розриву.

2.Знайти асимптоти.

3.Дослідити функцію на парність, непарність, періодичність.

4.Знайти точки перетину графіка функції з осями координат.

Другий етап (використання похідної першого порядку).

5.Дослідити функцію на монотонність і точки екстремуму.

Третій етап (використання похідної другого порядку).

6.Дослідити функцію на вгнутість, опуклість, точки перегину.

Четвертий етап.

7.Наносимо отримані характерні точки, асимптоти на координатну площину, будуємо графік функції.

Приклад 2. Дослідити функцію y = (x +1)(x − 2)2 і побудувати її графік.

Розв’язання. 1). D( y) = (−∞;+∞) .

2). Вертикальних асимптот немає, оскільки немає точок розриву. Дослідимо, чи має графік похилі асимптоти y = kx +l :

k = lim	y(x)	= lim	(x +1)(x − 2)2	∞		= lim((x − 2)	2	+ 2(x +1)(x − 2))= ∞
				=
	x		x
x→∞		x→∞		∞		x→∞
Отже, похилих асимптот графік також немає.
3). Оскільки y(−x) = (−x +1)(x + 2)2					≠ y(x) і y(−x) ≠ −y(x) , то функція

ні парна, ні непарна, тому графік функції не симетричний ні відносно осі Oy , ні відносно початку координат.

4). Знайдемо точки перетину графіка функції з осями координат.

299