6. Пределы и непрерывность

1. Если по некоторому закону каждому натуральному числу n поставлено в соответствие определенное число а_n то говорят, что задана числовая последовательность (а_n).

2. Число А называется пределом числовой последовательности (а_n )

если для любого ξ> 0 найдется такой номер N, зависящий от ξ, что для всех членов последовательности с номерами n > N верно неравенство

│a_n-A│<ξ(lim a_n=A

3. Число А называется пределом функции y=f(x) при х —> ∞ , если для любого ξ > 0 найдется также число S > О, зависящее от ξ, что для всех х таких, что |х| > S, будет верно неравенство │f(x)-A│<ξ (lim f(x)=A)

4. Функция а(х) называется бесконечно малой величиной при х —> х₀ (или х —> ∞ ), если lim а(х) = 0

6. Функция Fх) называется бесконечно большой величиной при х —> х₀, если для любого М > 0 найдется такое число δ > 0, зависяoщее от М, что для всех х #хо и удовлетворяющих условию |х - хо| < δ будет верно неравенство

│f(x)│>M(lim F(x)=∞.

Первый замечательный предел.

Lim sin x/x =1

u→0

Второй замечательный предел

Lim (1+1/x)^x=e lim (1+y)^1/y=e.

x→∞ y→0

Раскрытие неопределенностей различных типов

Далеко не всякая подстановка предельного значения в функцию вместо независимой переменной может сразу привес­ти к нахождению предела. Случаи, в которых подстановка предельно­го значения в функцию не дает значения предела, называют неопреде­ленностями; к ним относятся неопределенности видов

Устранить неопределенность удается часто с помощью алгебраи­ческих преобразований.

Семинар№6. Производная и дифференциал функции.

ПЗ №6. Дифференциальное исчисление функции одной переменной.

Производная. Дифференциал функции.

1. Разбор домашнего задания №4

2. Пользуясь определением производной, найти производный функций: 1) y=C, где C=const; 2) 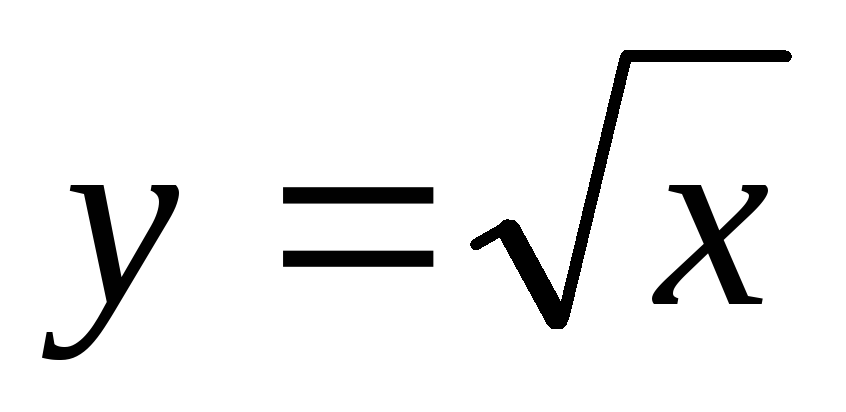; 3) y=sinx

Найти производные функций и вычислить их значения при x=2 и x=0:

1) ; 2); 3)

Найти производные следующих функций: 1) y=sin⁵x; 2) y=cos5x; 3) y=ln(x²+1); 4) y=7^8x-3; 5) y=(1-2x)⁵⁰

7.1. Определение производной.

1. Производной функции y = f(x) называется конечный предел приращения функции к приращению независимой переменной при стремлении последнего к нулю (при условии, что этот предел существует):

Δy f (x+Δx) – f (x)

y' = f'(x) = lim ― = lim ―――――― .

^Δx→0 Δx ^Δx→0 Δx

Если функция в точке x₀ (или на промежутке Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке Х).

2. Если функция y = f ' (x) дифференцируема в точке х₀ (или на промежутке Х), то она в этой точке непрерывна (или на промежутке Х). Если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке.

7.2. Правила дифференцирования.

Производные элементарных функций.

еренцирование явных функций

Правила дифференцирования:

с – постоянная, u = u (х), v = v (х) – дифференцируемые функции:

с' = 0; (7.2) (uvw)' = u'vw + uv'w + uvw'; (7.7)

х'= 1; (7.3) u'v - uv'

( u/ v)' = ―――――, v (х) ≠ 0; (7.8)

(u ± v)' = u' + v'; (7.4) v²

(u v)' = u'v + uv'; (7.5) сv

(с/ v)' = - ― , v (х) ≠ 0 (7.9)

(сu)' = сu'; (7.6) v²

Производная сложной функции. Если y = f (u), u = u (x), т.е. y = f [u (x)], где f (u) и u (x) имеют производные, то

y'= f ' (u) · u ' . (7.10)

Производная обратной функции. Если y = f (x) ― дифференцируемая и строго монотонная функция на промежутке Х, то функция, обратная к данной х = φ(y), также дифференцируема и ее производная определяется соотношением:

1

x'_y = ― , y'_x ≠ 0 . (7.11)

y'_x

Логарифмическая производная. Логарифмической производной функции y = f (x) называется производная от логарифма этой функции, т.е.

y' f'(x)

(lny)' = ― = ―― . (7.12)

Y f(x)

Формулы дифференцирования основных элементарных функций:

1 .(xⁿ)' = nx ^n-1; 7. (cos x)' = -sin x ;

1 1

2. (√x)' = ― , (х >0); 8. (tg x)' = ―― ;

2√x cos² x

1

3 .(e^x)' = e^x ; 9. (ctg x)'= - ―― ;

sin² x

(а^х)' = a^x 1na ; 1

10. (arcsin x)' = ――, (׀x׀<1);

√1-х²

4. (1nx)' = 1/х , (x>0); 1

11. (arccos x)' = - ――, (׀x׀<1);

√1-х²

1

5. (1og_ax)' = ―― , (х > 0, а >0); 12. (arctg x)' = 1/(1+х²) ;

х1na

6. (sin x)' = cos x ; 13. (arcctg х)' = 1/ (1+х²).

2. Дифференцирование неявных функций

Если зависимость между х и у задана в неявной форме уравнением F(x,y)=0, то для нахождения производной функции у необходимо продифференцировать по х обе части данного уравнения, рассматривая у как функцию от х. Из полученного уравнения первой степени (относительно у') находится у' .