
- •Глава II
- •2. Дискретные и непрерывные случайные величины
- •3. Законы распределения дискретной случайной
- •4. Функция распределения случайной величины, функция
- •5. Производящая функция дискретной случайной величины
- •6. Плотность распределения вероятностей
- •Тема 8. Числовые характеристики
- •1. Математическое ожидание случайной величины
- •2. Дисперсия случайной величины
- •3. Среднее квадратичное отклонение
- •4. Среднее квадратичное отклонение суммы
- •5. Одинаково распределённые взаимно
- •6. Мода и медиана, моменты случайных величин
- •7. Асимметрия и эксцесс, квантили
- •8. Производящая функция
- •Тема 9. Основные законы распределения
- •1. Биномиальный закон распределения (Закон Бернулли)
- •2. Распределение Пуассона
- •3. Геометрическое распределение
- •4. Гипергеометрическое распределения
- •5. Равномерный закон распределения
- •2. .
- •6. Показательный закон распределения
- •7. Функция надёжности, показательный закон надёжности
- •8. Характеристическое свойство показательного
- •9. Нормальный закон распределения
- •Тема 10. Предельные теоремы теории вероятностей
- •1. Неравенство Чебышева и Маркова
- •2. Теорема Чебышева (збч Чебышева)
- •3. Ещё раз о теореме Бернулли
- •4. Центральная предельная теорема
- •0,04, Т.Е..
- •5. Применение цпт
- •6. Примеры на применение нормального закона
7. Асимметрия и эксцесс, квантили
Коэффициентом асимметрии
(«скошенности»)
с.в.![]() называется
величина
называется
величина![]() ,
которая определяется равенством
,
которая определяется равенством
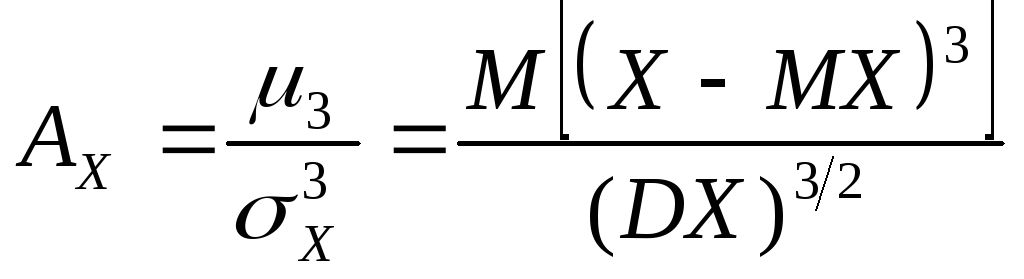
Величина
![]() характеризуется следующим образом:
характеризуется следующим образом:
Если
![]() то
график кривой распределения с.в.
то
график кривой распределения с.в.![]() более
полога справа от точки
более
полога справа от точки![]() (см. рис. 24 Письменный).
(см. рис. 24 Письменный).
Если
![]() то
график кривой распределения с.в.
то
график кривой распределения с.в.![]() более
полога слева от точки
более
полога слева от точки![]() (см. рис. 25 Письменный).
(см. рис. 25 Письменный).
Коэффициентом эксцесса
(«островершинность»)
с.в.![]() называется
величина
называется
величина![]() ,
которая определяется равенством
,
которая определяется равенством
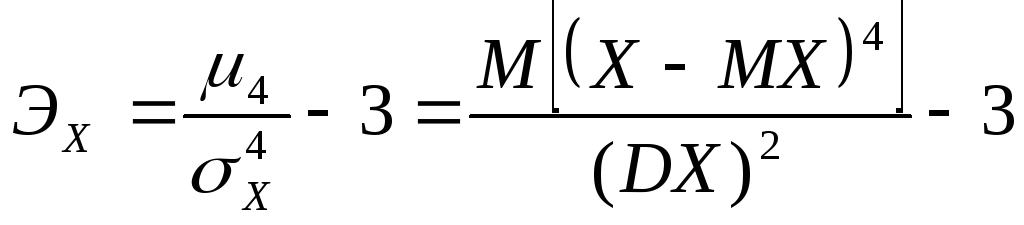 ,
,
Величина ![]() характеризует островершинность
или плосковершинность
распределения
случайной величины
характеризует островершинность
или плосковершинность
распределения
случайной величины
![]() .
.
Для нормального закона
распределения
![]() ;
остальные распределения сравниваются
с нормальным: если коэффициенты эксцесса
(островершинность )
;
остальные распределения сравниваются
с нормальным: если коэффициенты эксцесса
(островершинность )
![]() с.в.
с.в.![]() является
более «островершинные», а в случаях,
когда распределения «плосковершинные»
то имеют
является
более «островершинные», а в случаях,
когда распределения «плосковершинные»
то имеют ![]() .(рис.26,Письменный).
.(рис.26,Письменный).
Кроме рассмотренных выше
числовых характеристик с.в.![]() ,
в приложениях так же используются
понятия так называемые «квантили».
,
в приложениях так же используются
понятия так называемые «квантили».
Квантилю уровня
![]() с.в.
с.в.![]() называется
решение уравнения
называется
решение уравнения
![]() где
где![]() -некоторое
число,
-некоторое
число,![]() В приложениях квантили
В приложениях квантили![]() имеют
свои названия:нижняя
квантиль, медиана
(т.е.
имеют
свои названия:нижняя
квантиль, медиана
(т.е.![]() иверхняя квантиль
соответственно. Они делят числовую
прямую на четыре части, вероятности
попадания в каждой части равны числу
иверхняя квантиль
соответственно. Они делят числовую
прямую на четыре части, вероятности
попадания в каждой части равны числу
![]() .
.
(см. рис. 27 Письменный).
8. Производящая функция
Для вычисления важнейших числовых характеристик дискретных случайных величин с целыми неотрицательными значениями удобно пользоваться так называемыми производящими функциями (мы уже в теме 7, п.5, упоминали кратко о частных случаях производящих функций, которых просто можно назвать «многочленного вида»).Здесь они рассматриваются в виде степенных рядов, т.е это понятие обобщается для бесконечного числа слагаемых.
Рассмотрим д.с.в.![]() ,
которая принимает неотрицательные
целые значения
,
которая принимает неотрицательные
целые значения![]() с
соответствующими вероятностями
с
соответствующими вероятностями![]() .
.
Производящей функциейнеотрицательной целочисленной
д.с.в.![]() называется
функция, определённая равенством
называется
функция, определённая равенством
(36)
![]()
где
![]() комплексное число,
комплексное число,![]() Следует отметить, что для всех
Следует отметить, что для всех![]() ряд(36), определяющий производящую
функцию, равномерно сходится.
ряд(36), определяющий производящую
функцию, равномерно сходится.
Действительно,
![]() .
.
Замечание. Производящая функция
однозначно определяет распределения
с.в.![]() ,
так как, эти коэффициенты производят
данного степенного ряда, т.е.
,
так как, эти коэффициенты производят
данного степенного ряда, т.е.
(37)
![]()
Действительно, дифференцируя под знаком суммы (это действие законно в области обсолютной и равномерной сходимости функциональных рядов), получим
(38)![]()
![]() .
.
![]()
где
![]()
Отсюда легко заметить, что при
![]() все слагаемые в правой части (38), кроме
первого, обращаются нулю. Первое же
слагаемое равно
все слагаемые в правой части (38), кроме
первого, обращаются нулю. Первое же
слагаемое равно![]() Тем самым, равенство (37) получено.
Тем самым, равенство (37) получено.
Утверждение (о вычислении моментов).
Пусть неотрицательная целочисленная
случайная величина![]() имеет
момент
имеет
момент![]() го
порядка. Тогда справедливы равенства
го
порядка. Тогда справедливы равенства
(39)
![]() .
.
Доказательство леммы непосредственно
выводится из формулы (38), если в ней
положить
![]() .
Из этой леммы получим следующие
равенства.
.
Из этой леммы получим следующие
равенства.
Следствие. Справедливы равенства
(40)
![]() ;
;![]() ;
;
![]() ,
,
где
![]() соответственно первое и второе
производных от функции
соответственно первое и второе
производных от функции
![]() .
.
Доказательство. Первая формула
очевидна, т.к. согласно закону распределения
д.с.в.![]() «контроль»всегда должна
выполняться, т.е множество рассматриваемая
с.в формируется из полной группы событий,
также отметить, что когда с.в. конечная,
то множество её значений можно дополнить
до бесконечности с соответствующими
вероятностями равными нулю.
«контроль»всегда должна
выполняться, т.е множество рассматриваемая
с.в формируется из полной группы событий,
также отметить, что когда с.в. конечная,
то множество её значений можно дополнить
до бесконечности с соответствующими
вероятностями равными нулю.
Далее, дифференцируя один раз (![]() ),
по
),
по![]() производящую функцию
производящую функцию![]() ,
имеем равенство
,
имеем равенство
![]()
Теперь, в этом равенстве положим
![]() ,
тогда получим
,
тогда получим
![]() ,
,
где
![]()
- биномиальные коэффициенты. Следовательно,
![]() .
.
Взяв вторую производную от функции
![]() (т.е.
(т.е.![]() ),
а затем, положив в ней
),
а затем, положив в ней![]() получим:
получим:
![]()
где
![]() соответственно
начальные моменты 2-го и 1-го порядков.
Отсюда с учётом вычислительной формулы
(35) , получим;
соответственно
начальные моменты 2-го и 1-го порядков.
Отсюда с учётом вычислительной формулы
(35) , получим;
![]()
![]()
Следовательно,
![]() .
Утверждение полностью доказано.
.
Утверждение полностью доказано.
Полученные формулы (40) используются для нахождения м.о., дисперсии случайных величин.
Свойства производящих функций.
|
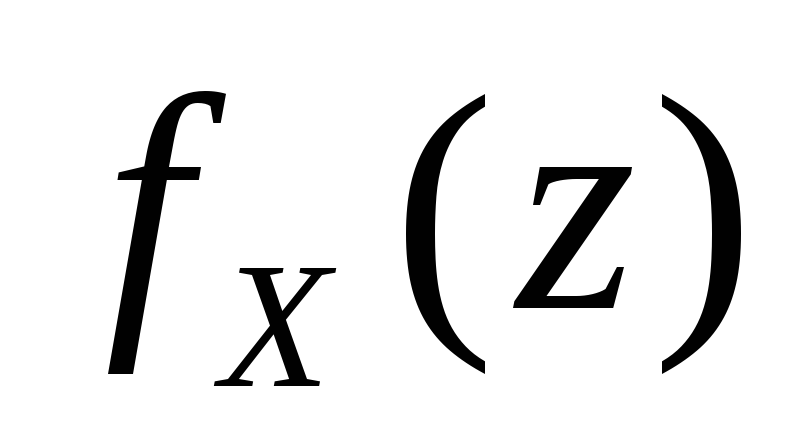 |
|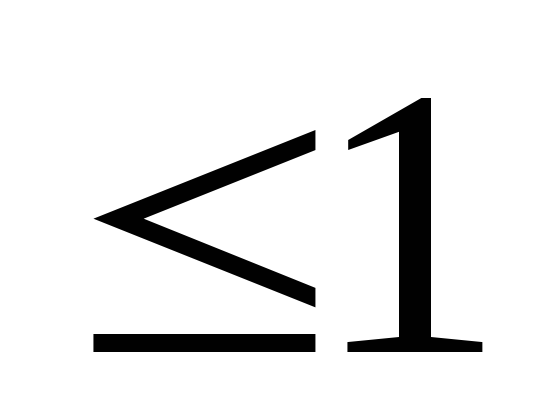 для
всех | z
|
для
всех | z
|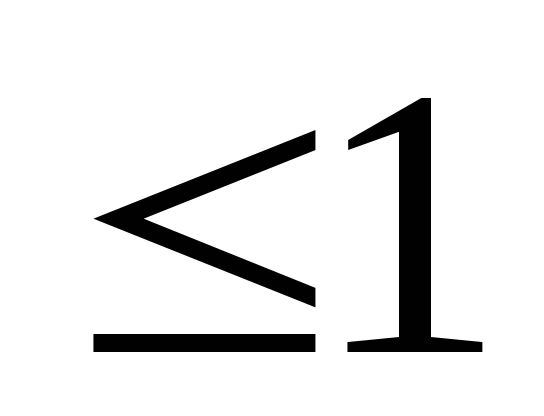 .
.
Действительно, так как д.с.в.![]() ,
неотрицательна, то по определению имеем
,
неотрицательна, то по определению имеем
|![]() |
|![]()
Для произвольных вещественных чисел
 и
и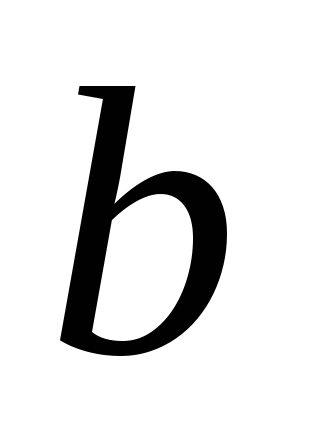 выполняется
равенство
выполняется
равенство
![]() .
.
Доказательство, на основании линейного свойства математического ожидания имеем
![]() ,
,
Отсюда, с учётом определения производящей функции, имеем
![]() .
.
Если
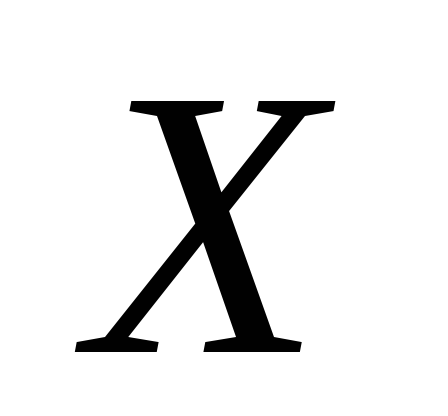 и
и независимые
случайные величины, то
независимые
случайные величины, то
![]() .
.
Доказательство, по свойству С.5. математического ожидания и определения производящей функции получим
![]() .
.
Поскольку,
![]() и
и![]() независимые случайные величины, то
независимые случайные величины, то
![]() ,
,
поэтому,
![]()
![]() =
=![]() .
.
Свойство 3. доказана.
Задача. Найти закон распределения
случайной величины![]() с
заданной производящей функции
с
заданной производящей функции![]()
Решение. Имеем,![]() следовательно, сравнивая с определением
функции
следовательно, сравнивая с определением
функции![]() ,будем иметь:
,будем иметь:
![]()
![]()
при
всех
![]() .
.
Пример 6. Производится три независимых выстрела по цели тремя расчётами:
1. Вероятности попадания по цели
каждого расчёта одинаковы и равны![]() .
.
Найти
а) с.в.![]() и
закон её распределения; б) Выписать
производящую функцию д.с.в.
и
закон её распределения; б) Выписать
производящую функцию д.с.в.![]()
в) Найдите
![]()
Решение.
1. Сначала составим закон распределения
с.в.![]() .
Найдём всевозможные случаи
.
Найдём всевозможные случаи
![]()
![]() .
.
Тем
самым, с. в.
![]() .
Соответственно с вероятностями попадания
в цель
.
Соответственно с вероятностями попадания
в цель![]() и непопадания
и непопадания![]() и с учетом независимости событий, будем
иметь:
и с учетом независимости событий, будем
иметь:
![]()
![]()
Следовательно,
закон распределения с.в.![]() имеет вид:
имеет вид:
|
|
0 |
1 |
2 |
3 |
|
|
0,001 |
0,027 |
0,243 |
0,729 |
Контроль:![]() .
.
Выпишем
производящую функцию случайной величины
![]()
![]()
Вычислим первое и второе производных этой функции:
![]()
![]()
![]()
Следовательно,
![]()
Задание. Решите аналогичную задачу,
с вероятностью![]() и сравните полученные результаты
рассеивания (значения дисперсий).
и сравните полученные результаты
рассеивания (значения дисперсий).
2. Пусть вероятность попадания расчётов
соответственно равны:![]()
а) Найдите множество значений с.в.![]() и
закон её распределения;
и
закон её распределения;
б) Выпишите производящую функцию
д.с.в.![]()
в) Найдите
![]()
