5. Одинаково распределённые взаимно

независимые случайные величины

Рассмотрим взаимно независимые случайные величины.которые имеют одинаковые распределения (т.е. одинаковые числовые характеристики: м.о., дисперсия и т.д.). Обозначим черезих среднее арифметическое

..

Сформулируем ниже три результата, устанавливающие связь между числовыми характеристиками величины и соответствующими числовыми характеристиками каждой отдельной величины.

I. Математическое ожидание среднего арифметического

одинаково распределенных взаимно независимых случайных величин, равно математическому ожиданию каждой из величин, т.е.

(20) .

Доказательство.На основании свойства м.о. и то, чтополучим

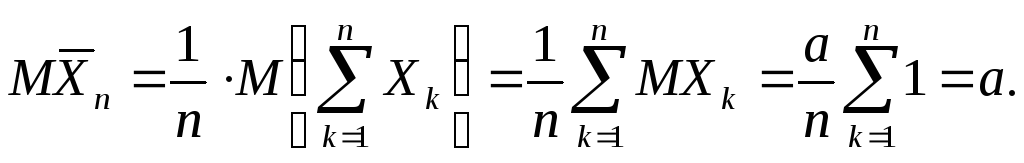
II.Дисперсия среднего арифметического одинаково распределенных взаимно независимых случайных величин враз меньше дисперсиикаждой из величин, т.е.

(21) .

Доказательство.На основании свойства дисперсии и то, что постоянный множитель можно вынести за знак дисперсии, возведённый в квадрат, и с учётом того, что дисперсия суммы независимых величин равна сумме дисперсий слагаемых, имеем

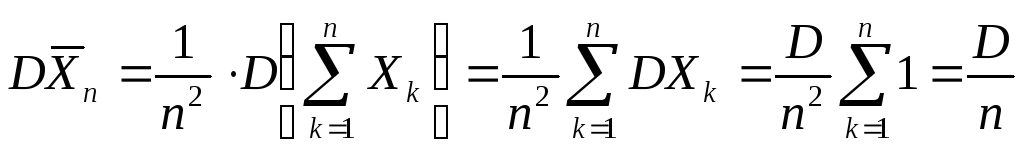
III. Среднее квадратическое отклонение среднего арифметического одинаково распределенных взаимно независимых случайных величин враз меньше среднего квадратичного отклонениякаждой из величин, т.е.

(22)

Доказательство непосредственно выводится из определения с.к.о. и формулы (22). Имеем:

Следствие. Пусть-взаимно независимыенормированныеслучайные величины, а, тогда

Таким образом, в этом случае при достаточно большом мера рассеивания с.в.стремится к нулю. Для пояснения полученных выводов рассмотрим следующий пример.

Пример 5.Обычно для измерения некоторой физической величины производят несколько измерений, а затем находят среднее арифметическое полученных чисел, и его принимают за приближенное значение измеряемой величины.

В предположении, что измерения производятся при одинаковых условиях, следует доказать:

1. Среднее арифметическое полученных чисел даёт более надёжный результат, чем отдельные измерения;

2. По мере увеличения число измерений надёжность подобного результата возрастает.

Решение. 1. Как правило, отдельные измерения дают неодинаковые значения измеряемой величины, при этом результат каждого измерения зависит от многих случайных причин (изменение температуры, колебания прибора и т.д.), которые заранее не могут быть полностью учтены.

Поэтому, возможные результаты проведенных измерений можно рассматривать как случайные величины(индексы указывают на номер измерения). Эти величины имеют одинаковое распределение вероятностей (т.е. измерение проводится по одной и той же методике и теми же приборами, а также при одинаковых комплексе условий).

Следовательно, их числовые характеристики – одинаковы. Кроме того, они взаимно независимы (т.е. результат каждого измерения не зависит от остальных).

Нам уже известно, что среднее арифметическое значение таких величин имеет «меньшее рассеивание», чем каждая отдельно взятая величина. Другими словами, среднее арифметическое значение оказывается более близким к истинному значению измеряемой величины, чем результат отдельного измерения. Это и означает, что среднее арифметическое нескольких измерений даёт более надёжный результат, по сравнению отдельное измерение.

2. Мы поняли, что при возрастании общего числа случайных величин, рассеивание (разброс) среднего арифметического убывает. Следовательно, с увеличением числа измерений среднее арифметическое нескольких измерений окажется всё ближе к истинному значению измеряемой величины. Таким образом, увеличивая число измерений, получают более надёжный результат.

Например, если среднее квадратическое отклонение отдельного измерения (скажем некоторого расстояния) , а всего произведеноизмерений, то среднее квадратическое отклонение среднего арифметического этих измерений равно лишь 1.

Действительно,

,

при любом целом положительном .

Если же взаимно независимыенормированныеслучайные величины с м, и число измерений равно, а, то

.

В этом примере мы видим, что среднее арифметическое нескольких измерений, как и следовало, ожидать, оказалось значительно близким к истинному значению измеряемой величины, чем результат отдельного измерения.

Отметим, что для любой случайной величины

.

Действительно, легко заметить, что если , то, а так же, еслии имеют одинаково распределёнными вероятностями, то. Поскольку, тои. Что и требовалось доказать.