
- •Глава II
- •2. Дискретные и непрерывные случайные величины
- •3. Законы распределения дискретной случайной
- •4. Функция распределения случайной величины, функция
- •5. Производящая функция дискретной случайной величины
- •6. Плотность распределения вероятностей
- •Тема 8. Числовые характеристики
- •1. Математическое ожидание случайной величины
- •2. Дисперсия случайной величины
- •3. Среднее квадратичное отклонение
- •4. Среднее квадратичное отклонение суммы
- •5. Одинаково распределённые взаимно
- •6. Мода и медиана, моменты случайных величин
- •7. Асимметрия и эксцесс, квантили
- •8. Производящая функция
- •Тема 9. Основные законы распределения
- •1. Биномиальный закон распределения (Закон Бернулли)
- •2. Распределение Пуассона
- •3. Геометрическое распределение
- •4. Гипергеометрическое распределения
- •5. Равномерный закон распределения
- •2. .
- •6. Показательный закон распределения
- •7. Функция надёжности, показательный закон надёжности
- •8. Характеристическое свойство показательного
- •9. Нормальный закон распределения
- •Тема 10. Предельные теоремы теории вероятностей
- •1. Неравенство Чебышева и Маркова
- •2. Теорема Чебышева (збч Чебышева)
- •3. Ещё раз о теореме Бернулли
- •4. Центральная предельная теорема
- •0,04, Т.Е..
- •5. Применение цпт
- •6. Примеры на применение нормального закона
6. Примеры на применение нормального закона
Пример
1.
Завод изготовляет шарики для подшипников.
Каждый шарик должен иметь один и тот
же диаметр
![]() .
Однако в силу ряда причин, неизбежных
в условиях массового производства,
фактический диаметр несколько отличается
от
величины
.
Однако в силу ряда причин, неизбежных
в условиях массового производства,
фактический диаметр несколько отличается
от
величины
![]() .
Обозначим через
.
Обозначим через![]() разность между фактическим диаметром
и числом
разность между фактическим диаметром
и числом![]() .
.
По
соображениям, изложенным в п. 10
предыдущего
параграфа, можно принять, что величина
![]() подчиняется нормальному закону
распределения с математическим ожиданием
подчиняется нормальному закону
распределения с математическим ожиданием![]() и некоторым
средним квадратичным отклонением
и некоторым
средним квадратичным отклонением
![]() (характеризующим
среднюю точность изготовления шариков).
(характеризующим
среднюю точность изготовления шариков).
Каждый
шарик, сойдя с конвейера, проходит
контроль. Последний состоит в том, что
шарик
пропускается через отверстия диаметром
![]() и
и![]() (рис.46
из
Солодовникова).
Все шарики, которые
свободно проходят через большое
отверстие, но застревают в меньшем,
поступают в готовую продукцию; остальные
шарики бракуются.
Найти вероятность того, что случайно
выбранный
с конвейера шарик будет забракован.
(рис.46
из
Солодовникова).
Все шарики, которые
свободно проходят через большое
отверстие, но застревают в меньшем,
поступают в готовую продукцию; остальные
шарики бракуются.
Найти вероятность того, что случайно
выбранный
с конвейера шарик будет забракован.









Нужно корректировать рисунок 46, из кн. Солодовникова.
Решение. Условием успешного прохождения шарика через контроль являетя выполнение неравенств
![]() .
.
Имеем (см. формулу (26)):
![]() .
.
Поэтому
вероятность того, что шарик окажется
бракованным, равна
![]() .
.
Пример
2.
Для определения точности измерительного
прибора
произведено
сравнение его показаний с показаниями
контрольного (высокоточного) прибора.
Это сравнение показало, что 75 %
всех ошибок данного прибора не превосходят
по абсолютной величине 2 мк. Считая, что
ошибка измерения подчиняется нормальному
закону с математическим ожиданием 0,
найти среднее квадратичное отклонение
![]() .
.
Решение.
Обозначим ошибку при измерении на
данном приборе через
![]() .
По
условию
.
По
условию
![]() есть случайная величина, подчиненная
нормальному закону распределения с
плотностью
есть случайная величина, подчиненная
нормальному закону распределения с
плотностью
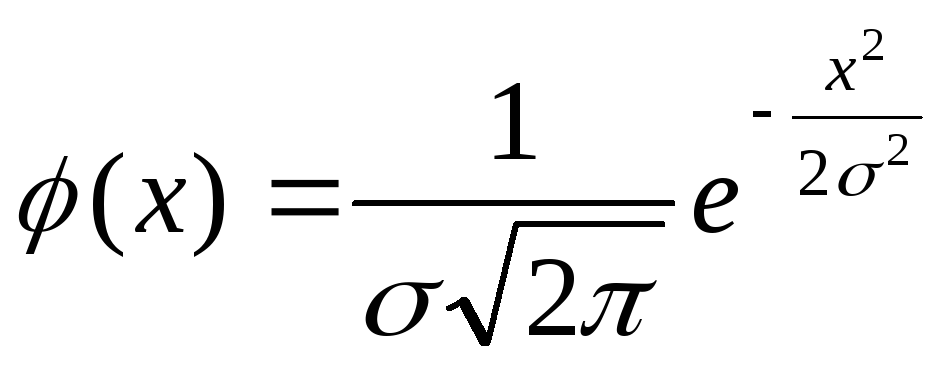 .
.
В
произведенной серии измерений событие
![]() имело частоту 0,75. Считая, что число
проделанных измерений достаточно
велико, и заменяя частоту вероятностью,
запишем:
имело частоту 0,75. Считая, что число
проделанных измерений достаточно
велико, и заменяя частоту вероятностью,
запишем:
![]() .
.
Отсюда
![]() или
или
![]() .
Решая уравнение
.
Решая уравнение![]() затем,
по таблице
значений
функции
затем,
по таблице
значений
функции
![]() находим.
находим.
![]() Откуда
Откуда
![]()
