2. Теорема Чебышева (збч Чебышева)

Основное утверждение ЗБЧ содержится в теореме Чебышева. В ней и других теоремах ЗБЧ используется понятие «сходимости случайных величин по вероятности». Определим это понятие:

Говорят, что случайные величины сходятся по вероятности к величине(случайной или неслучайной), если для любоговероятность событиядлястремиться к единице, т.е.

(14) (или).

Сходимость по вероятности символически обозначается:

(15) .

Замечание.Сходимость по вероятноститребует, чтобы неравенствовыполнялось для подавляющего количества членов последовательности. В теории пределах это понятие вводится несколько по - другому: для всех номеров последовательности начиная с некоторого номера,все члены последовательности должны принадлежать вокрестность предельной величиныа здесь дляпрактически все члены последовательности должны попасть вокрестность величины

Теорема 10. 5. (ЗБЧ в форме П.Л. Чебышева, 1886г).Если случайные величинынезависимы и существует положительное постоянное число, что

то для любоговыполняется неравенство

(16) ,

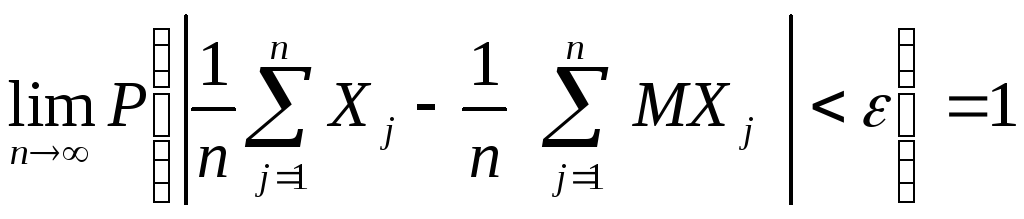т.е. среднее арифметическое этих случайных величин сходится по вероятности к среднему арифметическому их математического ожидания:

(17) .

Доказательство. Так както

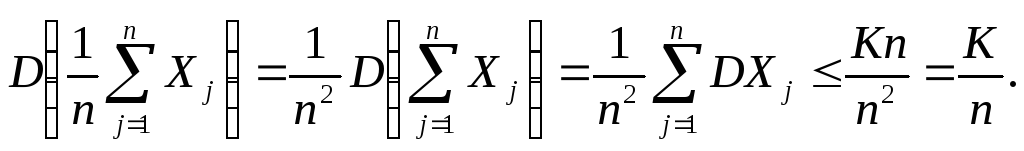
Применяем неравенство (второе неравенство из (12)), Чебышева к с.в. имеем

(18) .

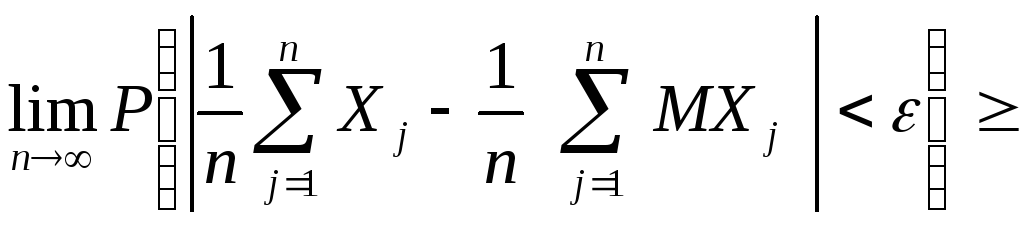
Переходя к пределу при с учётом того, что вероятность любого события не превышает 1, получаем равенство (16). Утверждение доказано.

Следствие. Если случайные величинынезависимы и одинаково распределены, т.е.то для любогосправедливо предельное равенство

(20) ,

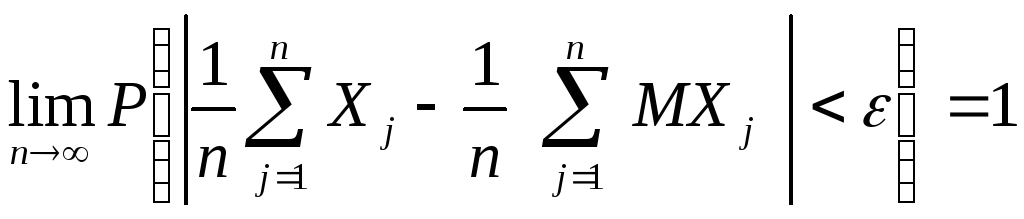т.е. среднее арифметическое с.в. сходится по вероятности к математическому ожиданию :

.

Проверка равенство (20) легко выводится на основании свойства м.о. и равенства

а также с учётом того, что дисперсия с.в. равны числу,т.е. ограничены. Поэтому можно применить ЗБЧ Чебышева.

Следствие (20) теоремы Чебышева обосновывает «принцип осредненного арифметического с.в.», часто используемое на практике.

Рассмотрим такой пример.Пусть произведенонезависимых измерений некоторой величины, истинное значение которой равно(оно неизвестно!). Результат каждого измерения есть с.в.Согласно следствию (20), и в качестве приближённого значения величиныможно взять среднее арифметическое результатов измерений:

Это равенство тем точнее, чем больше число измерений

На теореме Чебышева основан также широко применяемый в статистике выборочный метод, смысл которого в том, что о качестве большого количества однородного материала можно судить при небольшом числе его пробе.

Теорема Чебышева подтверждает связь между случайностью и необходимостью среднее значение случайной величины .

Пример 3.Глубина моря измеряется прибором, не имеющим систематической ошибки. Среднее квадратичное отклонение измерение не превосходит 15м. Сколько нужно сделать независимых измерений, чтобы с вероятностью не меньшей 0,9, можно было бы утверждать, что среднее арифметическое этих измерений отличаются от(глубины моря) по модулю меньше, чем на 5 м?

Решение. Обозначим черезрезультатынезависимых измерений глубины моря. Нужно найти число, которое удовлетворяет неравенству (18);

.

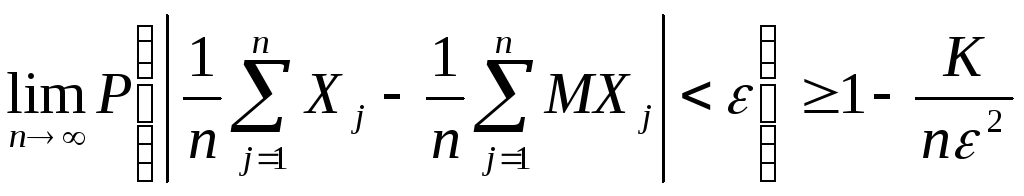где Это означает отсутствие при измерениях систематической ошибки (измерение проводятся с одинаковой точностью). По условию,так какм. Отсюда

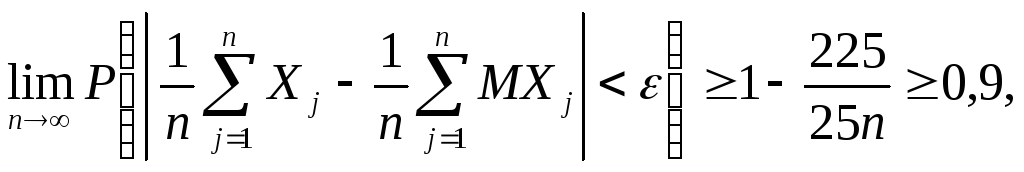
т.е. 0,1Следовательно, измерение следует провести не менее 90 раз.

Сущность теоремы Чебышева можно сказать такова:

«Среднее арифметическое достаточно большого количества независимых случайных величин (дисперсия которых равномерно ограничены) утрачивает характер случайности»

Это объясняется тем, что отклонения каждой из величин от своих м.о., т.е. могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погащаются. Другими словами, происходит между ними некоторая «интерференция», что указывает на объективные связи между случайностью и необходимостью. Тем самым, подтверждается справедливость философского учения - диалектического материализма.

Значение ЗБЧ Чебышева для практики коротко можно характеризовать в виде:

Приведём некоторые примеры применения ЗБЧ Чебышева к решению практических задач.

Традиционно на практике для измерения некоторой физической величины производят ряд измерений, составляют их среднее арифметическое и принимают его в качестве искомого размера измерения. Возникает естественный вопрос, «при каких условиях такой способ измерения можно считать правильным?» Ответ на такой вопрос даёт частный случай теорема Чебышева.

Действительно, рассмотрим результаты каждого измерения некоторого эксперимента как с.в. К исследованию этих величин можно применить теорему Чебышева, если:

1) они попарно независимы;

2) имеют одно и тоже математическое ожидание;

3) Дисперсия их равномерно ограничены.

Первое требование выполняется, если результат каждого испытания не зависит от результатов остальных. Второе требование выполняется, если измерения проведены без систематических ошибок (т.е. с точностью одного знака). В этом случае математические ожидания всех случайных величин одинаковы и равны истинному размеру . Третье требование выполняется, если измерительный прибор обеспечивает необходимую точность. Хотя при этом результаты отдельных измерений возможно различны, но мера рассеивание их ограниченно.

Если все указанные требования выполняются, мы вправе применять к результатам проведённого измерения теорему Чебышева, тогда при достаточно большом числе измерений вероятность неравенства

,

как угодно близко к единице. Другими словами, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое сколь угодно мало отличается от истинного значения измеряемой величины.

Предострожение. Ошибочно думать, что увеличивая число измерений, всегда можно достичь результат сколь угодно большой точности. Дело в том, что сам прибор может дать показания с точностью некоторой величины. Поэтому каждый из результатов измерений, а следовательно, и их среднее арифметическое будут получены лишь с точностью, не превышающей точности прибора.

Как уже было отмечено ранее, на теореме Чебышева базируется широко применяемый в статистике «выборочный метод», суть которого состоит в том, что по сравнительно небольшой выборке делают заключение о всей совокупности (так называемый «генеральной совокупности») исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, случайно отобранных из разных из разных месть кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчислимое сотнями. В качестве другого примера можно указать на процесс определение качества зерна по небольшой его пробе. И в этом случае объём случайно отобранных зёрен мало по сравнению со всей массой зерна, но само по себе оно достаточно велико.

Можно продолжит число таких примеров, но уже из приведённых можно заключить, что для практики теорема Чебышева имеет неоценимое значение.