Тема 10. Предельные теоремы теории вероятностей

Рассмотрим несколько утверждений и теорем из большой группы, так называемых предельных теорем теории вероятностей, устанавливающих связь между теоретическими и экспериментальными характеристиками случайных величин при достаточно большом числе испытаний над ними. Они составляют основу математической статистики. Предельные теоремы условно делят на две группы.

Первая группа теорем, называемая законом больших чисел (ЗБЧ), устанавливает устойчивость средних значений: при большом числе испытаний их средний результат перестаёт быть случайным и может быть предсказан с достаточной точностью. Одна из таких теорем (ЗБЧ в форме Я.Бернулли, Т.6 п.7) нами уже была рассмотрена в качестве применения интегральной формулы Муавра-Лапласса. Этот закон теоретически обосновывает свойство устойчивости относительной частоты появления некоторого события раз прииспытаниях по схеме Бернулли.

Вторая группа теорем, называемая центральной предельной теоремой (ЦПТ) устанавливает при некоторых сравнительно широких условиях, суммарное поведение достаточно большого числа с.в. почти утрачивает случайный характер и становится закономерным, т.е. устанавливается условий, при которых закон распределения суммы большого числа случайных величин неограниченно приближается к нормальному закону.

Для практики важно знание условий, при выполнении которых совокупное действие многих случайных причин приводят к результату, почти не зависящему от случая, и позволяет предвидет ход событий. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Бернулли и Чебышева, Маркова и др.

В начале рассмотрим неравенство Чебышева, которое можно применять:

а) для грубой оценки вероятностей событий, связанных с случайными величинами, распределение которых неизвестно;

б) для доказательства ряда теорем ЗБЧ.

1. Неравенство Чебышева и Маркова

Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин.

1. Пусть 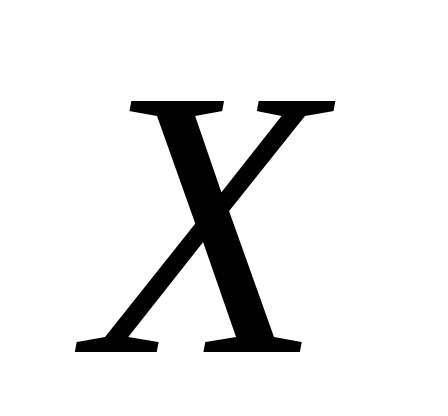- дискретная случайная величина с заданной таблицей распределения

			...
			...

Контроль-

Поставим перед собой задачу: «оценить вероятность того, что отклонение д.с.в. от её м.о. по абсолютной величине не перевешает положительного числа». Имеет место утверждение

Теорема 10.1. (неравенство Чебышева д. с. в.). Если дискретная случайная величина имеет м.о.и дисперсиюто для любогосправедливо неравенство

(1)

Доказательство. Поскольку событияипротивоположные, то сумма их вероятностей равна единице, т.е.

(2) .

Отсюда интересующая нас вероятность

(3) ,

Следовательно, задача сводится к вычислению вероятности

Далее, напишем выражение дисперсии для с.в. : по определению для д.с.в.

В левой части этого выражения отбросим все слагаемые. у которых (для оставшихся слагаемых), в результате чего сумма только уменьшиться. Без ограничения общности этими слагаемыми можно выбрать первыеслагаемых в сумме.

Таким образом, , т.е.

(4)

Заметим, что обе части неравенства положительны, поэтому, возведя их в квадрат, получим равносильные неравенствадля всех

Воспользуемся этим замечанием в правой части нашей суммы, получим

(5) ).

По теореме сложения, сумма вероятностей - есть вероятность того, что с.в.примет одно (безразлично какое) из значенийа при любом из них отклонение удовлетворяет неравенствуОтсюда следует, что суммавыражает вероятность. Это соображение позволяет переписать неравенство (5) в виде:

или

.

Следовательно, согласно равенствам (2) и (3) получим доказательство неравенство (1).

Замечание. Неравенство Чебышева (1) можно переписать в другом виде:

(6)

Отметим, что для практики неравенство Чебышева имеет ограниченное значение, поскольку часто даёт грубую, а иногда и тривиальную (не представляющую интереса) оценку. Например, если тоэтим самым Неравенство Чебышева в этих случаях лишь потверждает того, что любая вероятность выражается неотрицательным числом.

Неравенство Чебышева в частности, для случайной величины имеющей биномиальное распределение с м.о.и дисперсией(см.Т.9., теорема 1), принимает вид

(7)

В том числе, для отклонения частотысобытия внезависимых испытаниях, в каждом из которых оно может произойти с вероятностьюи дисперсией, неравенство Чебышева имеет вид:

(8)

Пример 1. Оценить с помощью неравенство (1) вероятность того, что отклонение д.с.в.

от своего математического ожидания будет меньше .

Решение. Положим в формуле (1)получим оценку снизу

Оценка сверху, как известно ( п.9. формула (45)), называется «правилом трёх сигм» для с.в.и эта вероятность была равнаКак легко заметить, неравенство Чебышева даёт результат несколько слабее. В общем случае получаем неравенство

(9) .

Пример 2. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за времяравна 0,05. С помощью неравенство Чебышева оценить вероятности того, что абсолютная величина разности между числом отказавших элементов и средним числом (м.о.) отказов за времяоткажется: а) меньше двух; б) не меньше двух.

Решение. а) Пустьобозначает дискретную случайную величину, выражающую число отказавших элементов за время. Тогда по закону Бернулли (

По неравенству Чебышева имеем

б) События и противоположны, поэтому сумма их вероятностей равна единице. Следовательно,

2. Пусть н.с.в.задана со своей функцией распределения вероятности. Тогда справедливо утверждение

Теорема 10.2. (неравенство Чебышева для н. с. в.). Если непрерывная случайная величина с плотностьюимеет м.о.и дисперсиюто для любогосправедливо неравенство

(10)

Доказательство. Вероятностьесть вероятность попадания н.с.в.в область, лежащую вне промежутка Поэтому имеем

Заметим, что область интегрирования можно записать в виде, откуда следует, что. Следовательно,

=.

Так как подынтегральная функция неотрицательна, то расширяя пределы интегрирования получим неравенство

.

Таким образом, из двух последних формул получим

.

Утверждение доказано.

Это же неравенство можно записать (в силу равенства +=1) также и в другой форме:

(11)

Теперь объединяя обе теоремы, сформулируем неравенство Чебышева в общем виде.

Теорема 10.3. Если случайная величина имеет м.о.и дисперсию,то для любогосправедливы неравенства

1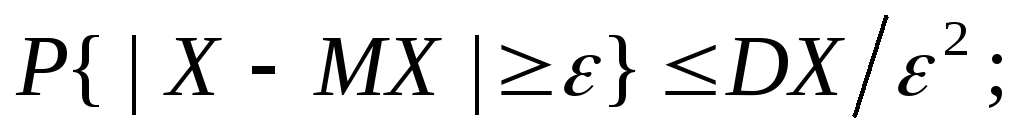2. 1. 2..

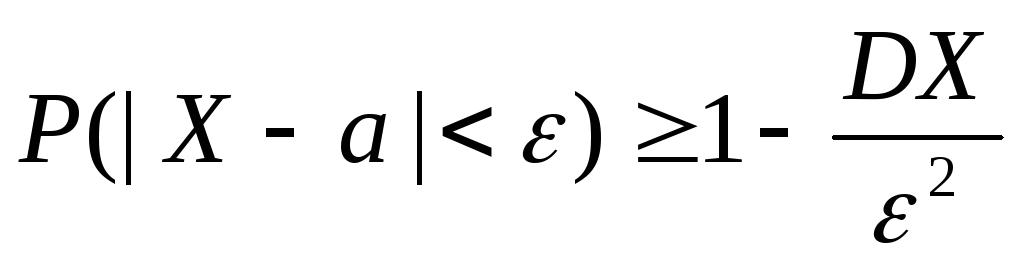Замечание. Неравенство Чебышева имеет для практики ограниченное значение, поскольку часто даёт грубую оценку, а иногда тривиальную (не представляющего интереса) оценку. Например, еслии, следовательно,то. Таким образом, в этом случае неравенство Чебышева указывает лишь на то, что вероятность отклонения есть неотрицательное число, а это и без того очевидно, так как любая вероятность выражается неотрицательным числом.

Рассмотрим ещё одно неравенство для неотрицательно определённых случайных величин.

Теорема 10.4. (Неравенство Маркова). Если неотрицательная случайная величина имеет м.о., то для любогосправедливо неравенство

13. 1. 2..

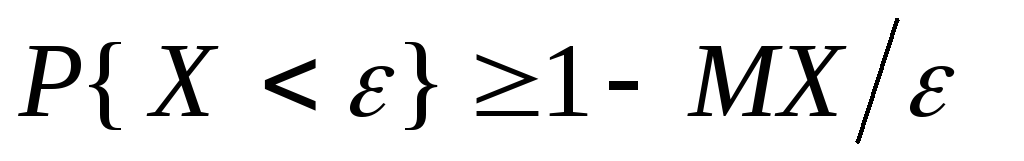Доказательство. Проверим справедливости неравенств (12) для н.с.вс функцией плотностью. Имеем

Так как

то получим и второе неравенство.