
- •Вища математика
- •Тематичні індивідуальні завдання та приклади розв’язання типових завдань з курсу „Вища математика”
- •Харків 2009
- •Передмова
- •§1. Елементи лінійної алгебри Завдання 1. В задачах варіантів 125 обчислити визначник четвертого порядку
- •Завдання 2.
- •Розв’язання типового варіанта.
- •Якщо матриця а є невиродженою, то
- •§2. Елементи векторної алгебри Завдання 3.
- •Розв’язання типового варіанта.
- •§3. Аналітична геометрія
- •Розв’язання типового варіанта
- •4. Дано координати точок: а (–1; 4; 2); в(0; 3; 3); с(4; –5; 3) і м(1; –3; 5).
- •§4. Вступ до математичного аналізу
- •Розв’язання типового варіанта.
- •2.Знайти границі:
- •3. Знайти границю
- •§5. Диференціальне числення функції однієї змінної
- •Розв’язання типового варіанта
- •1.Знайти похідні функцій:
- •§6. Функції багатьох змінних
- •§7. Інтегральне числення функції однієї змінної
- •Розв’язання типового варіанта
- •§8. Диференціальні рівняння
- •Розв’язання типового варіанта.
- •Дане рівняння приймає вигляд
- •Відповідне однорідне рівняння
- •Підставляючи , ,в дане рівняння, маємо
- •Розв’язуючи систему, знаходимо
- •§9. Ряди
- •Розв’язання типового варіанта
- •§10. Теорія ймовірностей та математичної статистики
- •Вихідні дані до задач
- •Список літератури
- •Вища математика
- •Тематичні індивідуальні завдання та приклади розв’язання типових завдань з курсу „Вища математика”
- •Харківський державний університет харчування та торгівлі.
Відповідне однорідне рівняння
![]()
має характеристичне
рівняння
![]() ,
корені якого дійсні і рівні, тобто
,
корені якого дійсні і рівні, тобто![]() .
Загальний розв’язок цього рівняння
.
Загальний розв’язок цього рівняння
![]() .
.
Частинний розв’язок неоднорідного рівняння шукаємо у вигляді
![]() .
.
Послідовно
диференціюючи ![]() ,
знаходимо
,
знаходимо
![]() та
та![]() :
:
![]() ;
;
![]() .
.
Підставляючи , ,в дане рівняння, маємо
![]() або
або
![]() .
.
Прирівнюючи
коефіцієнти при
![]() і
і![]() правої і лівої частин рівняння, отримаємо
систему двох рівнянь відносно шуканих
коефіцієнтівА
і В.
правої і лівої частин рівняння, отримаємо
систему двох рівнянь відносно шуканих
коефіцієнтівА
і В.
Маємо:
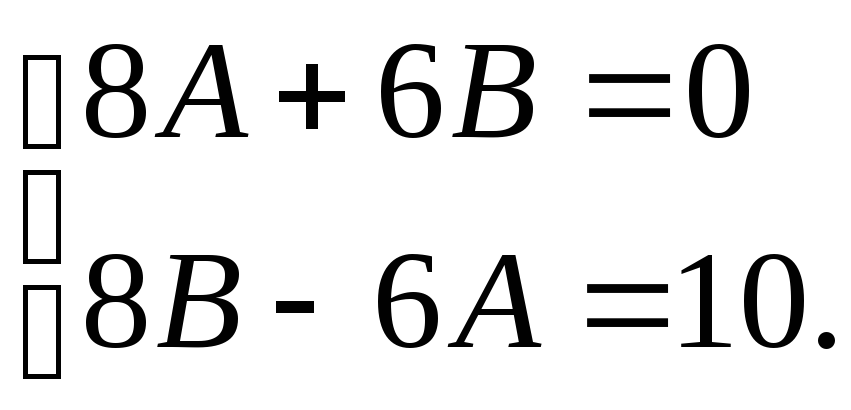
Розв’язуючи систему, знаходимо
![]() ;
;
![]() .
.
Отже,
![]() .
.
Звідси загальний розв’язок даного рівняння
![]() .
.
Щоб знайти частинний розв’язок,
що задовольняє початковим умовам,
попередньо знаходимо похідну
![]()
![]() .
.
За умовою
![]() ;
;![]() ,
тоді
,
тоді
![]() ,
звідки
,
звідки
![]() ;
;
![]() ,
звідки
,
звідки
![]() .
.
Підставляючи отримані значення
довільних сталих
![]() і
і![]() в загальний розв’язок, маємо
в загальний розв’язок, маємо
![]() шуканий частинний розв’язок.
◄
шуканий частинний розв’язок.
◄
§9. Ряди
Завдання 23. В задачах варіантів 125 дослідити на збіжність числові ряди.
1.
![]() . 2.
. 2.![]() . 3.
. 3.![]() .
.
4.
![]() . 5.
. 5.![]() . 6.
. 6.![]() .
.
7.
![]() . 8.
. 8.![]() . 9.
. 9. .
.
10.
![]() . 11.
. 11.![]() . 12.
. 12.![]() .
.
13.
![]() . 14.
. 14.![]() . 15.
. 15.![]() .
.
16.
![]() . 17.
. 17.![]() . 18.
. 18.![]() .
.
19.
![]() . 20.
. 20.![]() . 21.
. 21.![]() .
.
22.
![]() . 23.
. 23.![]() . 24.
. 24.![]() .
.
25.
![]() .
.
Завдання 24. В задачах варіантів 125 дослідити на збіжність знакопереміжні ряди
1.
![]() . 2.
. 2.![]() . 3.
. 3.![]() .
.
4.
![]() . 5.
. 5.![]() . 6.
. 6.![]() .
.
7.
![]() . 8.
. 8.![]() . 9.
. 9.![]() .
.
10.
![]() . 11.
. 11.![]() . 12.
. 12.![]() .
.
13.
![]() . 14.
. 14.![]() . 15.
. 15.![]() .
.
16.
![]() . 17.
. 17.![]() . 18.
. 18.![]() .
.
19.
![]() . 20.
. 20.![]() . 21.
. 21.![]() .
.
22.
![]() . 23.
. 23.![]() . 24.
. 24.![]() .
.
25.
![]() .
.
Завдання 25.
В задачах варіантів 1 - 25 знайти інтервал збіжності степеневого ряду, при цьому з`ясувати питання про його збіжність на кінцях інтервалу.
1.
![]() . 2.
. 2.
![]() . 3.
. 3.
![]() .
.
4.
![]() . 5.
. 5.
![]() . 6.
. 6.
![]() .
.
.7.
![]() . 8.
. 8.
![]() . 9.
. 9.
![]() .
.
10.
![]() . 11.
. 11.
![]() . 12.
. 12.
![]() .
.
13.
![]() . 14.
. 14.
![]() . 15.
. 15.
![]() .
.
16.
![]() . 17.
. 17.
![]() . 18.
. 18.
![]() .
.
19.
![]() . 20.
. 20.
![]() . 21.
. 21.
![]() .
.
22.
![]() . 23.
. 23.
![]() . 24.
. 24.
![]() .
.
25.
![]() .
.
Завдання 26.
В задачах варіантів 125 обчислити визначний інтеграл з точністю до 0,001 шляхом попереднього розкладання підінтегральної функції у степеневий ряд.
1.
![]() . 2.
. 2. . 3.
. 3. .
.
4.
![]() . 5.
. 5.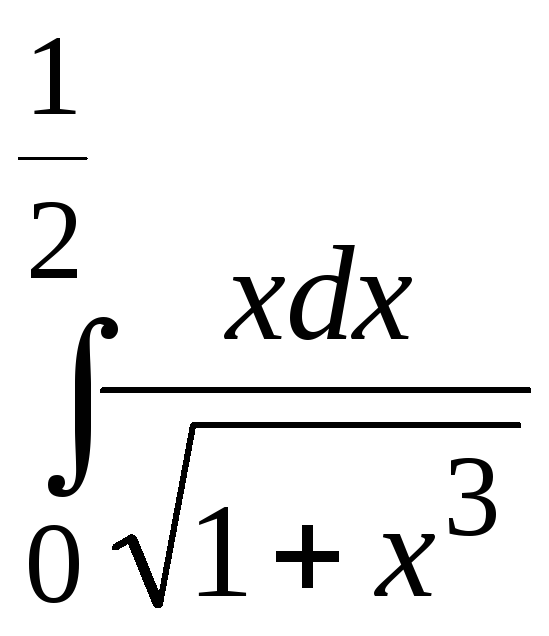 . 6.
. 6. .
.
7.
 . 8.
. 8.![]() . 9.
. 9.![]() .
.
10.
 . 11.
. 11. . 12.
. 12.![]() .
.
13.
 . 14.
. 14.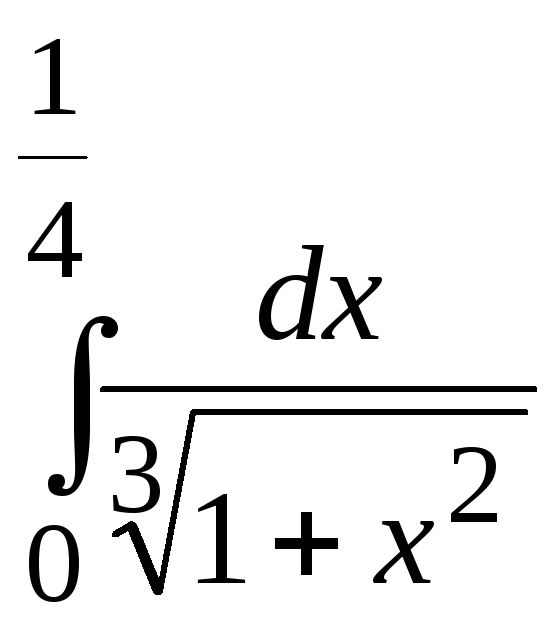 . 15.
. 15.![]() .
.
16.
 . 17.
. 17. . 18.
. 18.![]() .
.
19.
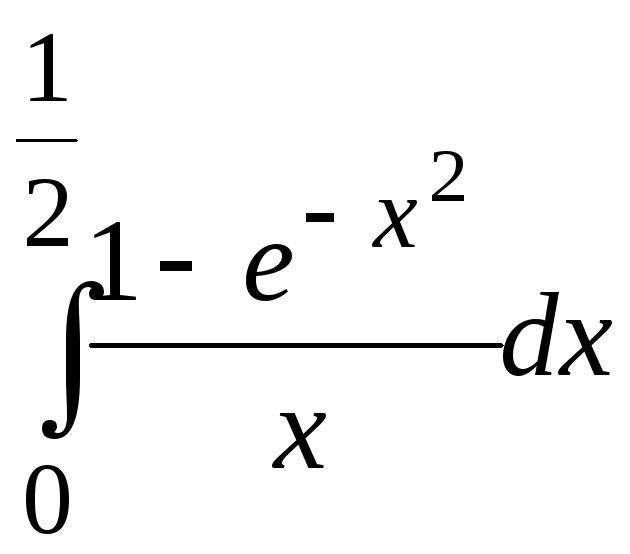 . 20.
. 20. . 21.
. 21. .
.
22.
 . 23.
. 23. . 24.
. 24. .
.
25.
 .
.
Завдання 27.
В задачах варіантів 125 обчислити наближене значення заданої величини з точністю до 0,0001, використовуючи відомі розклади відповідних функцій в ряд Маклорена.
1.
![]() . 2.
. 2.![]() . 3.
. 3.![]() . 4.
. 4.![]() .
.
5.
![]() . 6.
. 6.![]() . 7.
. 7.![]() . 8.
. 8.![]() .
.
9.
![]() . 10.
. 10.![]() . 11.
. 11.![]() . 12.
. 12.![]() .
.
13.
![]() . 14.
. 14.![]() . 15.
. 15.![]() . 16.
. 16.![]() .
.
17.
![]() . 18.
. 18.![]() . 19.
. 19.![]() . 20.
. 20.![]() .
.
21.
![]() . 22.
. 22.![]() . 23.
. 23.![]() . 24.
. 24.![]() .
.
25.
![]() .
.
Розв’язання типового варіанта
1. Знайти область збіжності степеневого ряду
![]()
► Даний степеневий ряд можна записати так:
![]() (11.20)
(11.20)
Застосуємо ознаку Даламбера:
![]() .
.
Як видно, ряд буде збігатись для тих значень х, для яких
![]() <1,
або
<1,
або![]() .
.
Дослідимо збіжність ряду на кінцях інтервалу.
При x=![]() ,
маємо числовий ряд:
,
маємо числовий ряд:
![]() . (11.21)
. (11.21)
Ряд (11.21) є знакопереміжним. У силу ознаки Лейбніца даний ряд збігається, бо
1)
![]() >
>![]() >
>![]() >
>![]() >…2)
>…2)![]() .
.
При x=![]() маємо числовий ряд
маємо числовий ряд
![]() ...
. (11.22)
...
. (11.22)
Ряд
(11.22) розбігається (для цього достатньо
порівняти його з гармонічним рядом
![]() .
.
Отже,
значення x =![]() не належить області збіжності даного
ряду.
не належить області збіжності даного
ряду.
Таким
чином, ![]()
область збіжності досліджуваного ряду.
область збіжності досліджуваного ряду.
2.
Обчислити визначений інтеграл
 з точністю до 0,001.
з точністю до 0,001.
► Обчислимо даний інтеграл наближено за допомогою рядів. Відомо, що
![]() .
.
Тоді
![]() ;
;
![]() .
.
Маємо
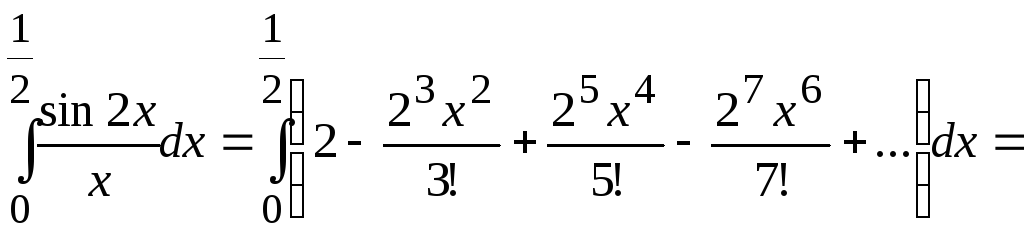
![]()
![]() .
.
Отримано знакопереміжний числовий ряд, який задовольняє умовам теореми Лейбниця. Оскільки четвертий член цього ряду за абсолютним значенням менше ніж 0,001, достатньо обмежитись сумою перших трьох членів. Отже
 .
◄
.
◄
3. Обчислити
наближено
![]() з точністю до 0,0001.
з точністю до 0,0001.
► Скористаємось формулою
![]() ;
;
який є збіжним при
![]() .
.
Запишемо заданий вираз у вигляді
![]() .
.
Для функції
![]() маємо наступний розклад
маємо наступний розклад

![]()
Підставляючи замість х
число
![]() ,
отримає числовий ряд
,
отримає числовий ряд
![]()
Маємо знакопереміжний числовий ряд. Щоб обчислити значення функції з точністю 0,0001, необхідно, щоб перший член, що відкидається, був менш, ніж 0,0001. Неважко обчислити, що
![]() .
.
Отже,
![]() .
.
