Розділ іу. Диференціальне числення

ТЕМА 14: Похідна функції. Геометричний, економічний сенс похідної. Зв’язок з неперервністю. Арифметичні теореми. Похідна складеної, оберненої функції. Таблиця похідних основних елементарних функцій. Логарифмічне диференціювання, похідна неявної функції. Диференціал. Геометричний сенс, інваріантність форми диференціалу. Похідні та диференціали вищих порядків.

Похідна функції. Геометричний, економічний сенс похідної. Зв’язок з неперервністю.

Нехай функція на деякій множині . Виберемо точкуі надамо приріст аргументу. Тоді функція набуде приріст .

Означення. Похідною функції за аргументом в точціназивається границя відношення приросту функції до віповідного приросту аргументу, коли останній прямує до нуля (якщо розглянута границя існує).

Позначається: .

Нагадаємо геометричний, фізичний і економічний зміст похідної:

1. Похідна дорівнює кутовому коефіцієнту дотичної, проведеної до графіку функції в точці з абсцисою .

2. Якщо функція визначає залежність пройденого матеріальною точкою шляху на момент часу(закон рівномірного руху точки), то похіднадорівнює швидкості точки в момент.

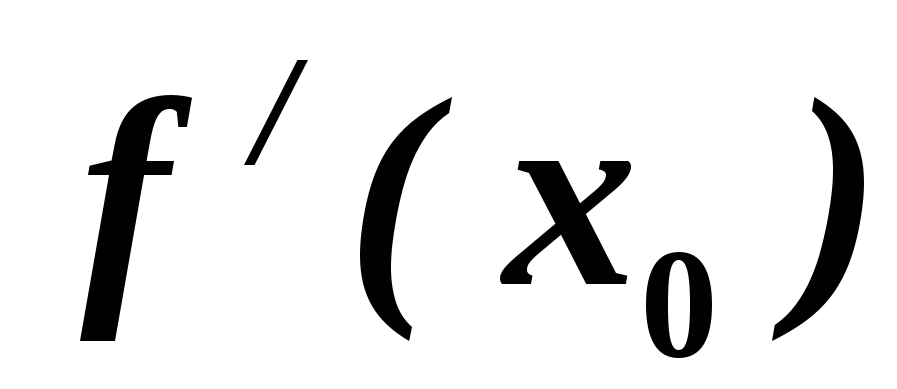3. Якщо функція визначає залежність витрат виробництва від об’ємувиробленої продукції, то похіднадорівнює граничним витратам виробництва (приблизно рівним витратам на випуск-ої одиниці продукції).

Означення. Якщо функція має похідну в точці , то вона називаєтьсядиференційовною в цій точці.

Теорема. Якщо функція диференційовна в точці , то вона в цій точці неперервна.

Доведення: Так як функція має похідну в точці, то за означенням існує границя . За теоремою про зв’язок збіжної та нескінченно малої привеличина- НМ. Звідси- НМ за властивостями НМ.

Отримали , а за означенням це означає, що функція неперервна в точці . Теорема доведена.

Зауваження: Обернене твердження взагалі кажучи невірне. Функція може бути неперервною в точці, але похідна в цій точці може не існувати.

Наприклад, розглянемо функцію . Ця функція в точцінеперервна, але похідна в цій точці не існує. Покажемо це:

, а За означенням: .

x

При розкритті модуля доведеться знаходити односторонні границі:

при , тому;

при , тому.

Односторонні границі існують, але не співпадають, тому границя не існує(порушується єдиність), а отже, не існує похідна функціїв точці.

Приклад показує, що графіком диференційовної функції повинна бути гладка крива (у якої немає кутових точок).

Арифметичні теореми. Похідна складеної, оберненої функції. Таблиця похідних основних елементарних функцій. Логарифмічне диференціювання, похідна неявної функції.

Теорема 1. Нехай функції ,диференційовні в точці. Тоді їх алгебраїчна суматакож диференційовна в точці, причому.

Доведення. За означенням:

, оскільки ,диференційовні в точці. Теорему доведено.

Теорема 2. Нехай функції ,диференційовні в точці. Тоді їх добутоктакож диференційовна в точціфункція, причому.

Доведення. За означенням:

.

В чисельнику віднімемо і додамо добуток , перегрупуємо доданки та винесемо спільні множники:

, оскільки ,диференційовні в точці (а значить – неперервні, тому ). Теорему доведено.

Наслідок. Сталий множник виноситься за знак похідної, тобто:

.

Теорема 3. Нехай функції ,диференційовні в точціі. Тоді їх часткатакож диференційовна в точціфункція, причому.

Доведення.

Теорема (похідна складеної функції). Нехай складена функція визначена на множині. Якщо функціядиференційовна в точці, а зовнішня функція диференційовна в точці , то складена функціядиференційовна в точціі її похідна знаходиться за формулою:

,

тобто похідна складеної функції дорівнює добутку похідної зовнішньої функції на похідну її аргументу (внутрішньої функції).

Доведення. За означенням . Поділимо і домножимо на приріст, який прямує до нуля при(це випливає із диференційовності, а значить, і неперервності функції). Дістанемо:

. Теорему доведено.

Теорема (про похідну оберненої функції). Якщо функція диференційовна в точці і, то обернена функція:

1. існує в деякому околі точки ;

2. диференційовна в точці ,причому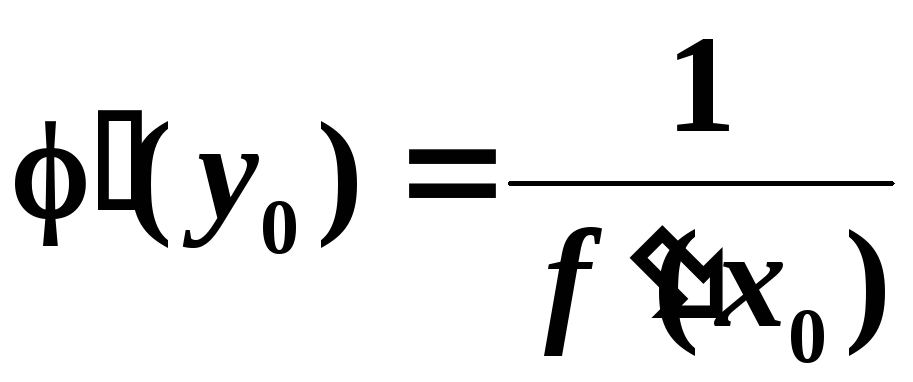, тобто похідна оберненої функції дорівнює оберненій величині похідної даної функції.

Таблиця похідних основних елементарних функцій

1. Похідна сталої дорівнює нулю: .

2. Похідна степеневої функції: , зокрема.

3. Похідна показникової функції: , зокрема.

4. Похідна логарифмічної функції: , зокрема .

Похідні тригонометричних функцій.

5. .

6. .

7. .

8. .

Похідні обернених тригонометричних функцій.

9. .

10. .

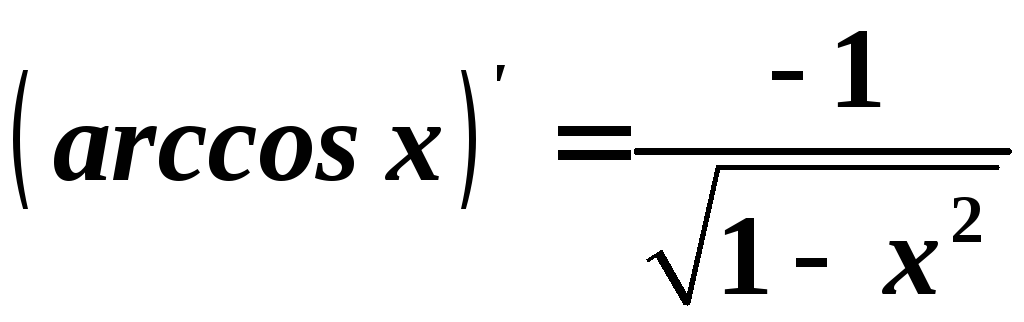11. .

12. .

Доведемо деякі із табличних похідних. При цьому будемо користуватися означенням похідної та доведеними вище теоремами.

1. Розглянемо похідну сталої функції . За означенням:

.

5. Розглянемо похідну функції . За означенням:

.

При : із чудової границі випливає, що функція- НМ, еквівалентна аргументу, а. Тому:

.

7. Розглянемо похідну функції . За арифметичними теоремами та враховуючи похідні функцій, дістанемо:

11. Розглянемо похідну функції , яка є оберненою для функції. За теоремою про похідну оберненої функції, враховуючи, що, маємо:

.

Приклади:

Знайти похідні функцій:

а) .

Розв’язування: за арифметичними теоремами (похідна суми та добутку функцій)

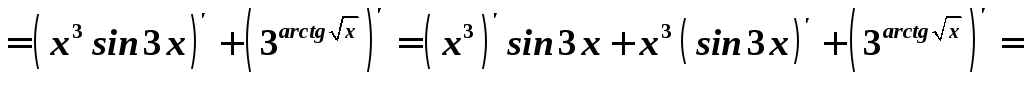
за таблицею та правилом диференціювання складеної функції, враховуючи, що зовнішніми є функції , маємо

залишились: похідна , а також похідна складеної функції, у якої зовнішня функція

оскільки похідна степеневої функції , остаточно дістаємо

.

б) .

Розв’язування: за арифметичними теоремами (похідна різниці та частки)

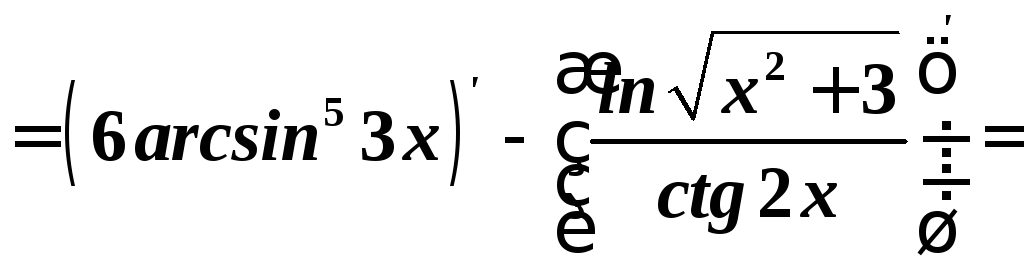
за таблицею та правилом диференціювання складеної функції, враховуючи, що зовнішніми є функції , маємо

за теоремою про похідну складеної функції (зовнішні функції: )

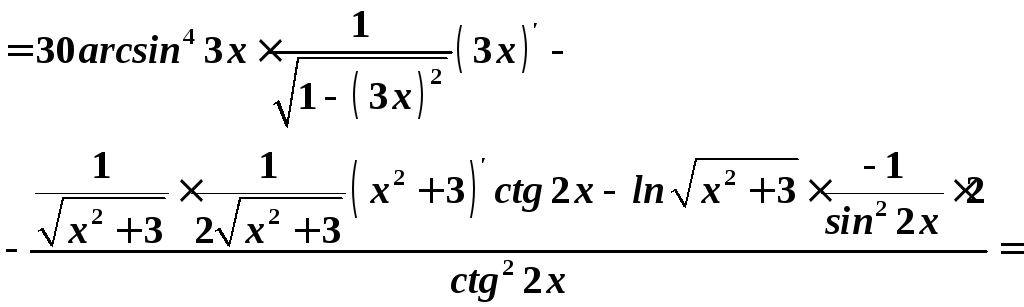
остаточно, із врахуванням спрощень, дістаємо

.