Методом елементарних перетворень.

1. Перестановкою рядків або стовпців (при необхідності) вибираємо перший діагональний елемент матриці , який назвемоключовим (головним, розв’язувальним).

2. У наступній матриці ключовий рядок переписується без змін, а всі елементи ключового стовпця замінюються нулями.

3. Усі інші елементи, які розташовані під ключовим рядком та праворуч ключового стовпця матриці, знаходяться за правилом „прямокутника”. А саме, якщо – ключовий елемент, то в новій матриці елементзнаходиться за формулою, яку можна зобразити

у вигляді „прямокутника”:

4. Здійснюється перехід до наступного кроку (вибираємо наступний ключовий діагональний елемент ).

Таким чином, за фіксовану кількість кроків матриця зводиться до трикутної (або до вигляду трапеції, яку відкиданням «зайвих» стовпців, замінюємо еквівалентною трикутною матрицею).

Приклад. Обчислити ранг матриці.

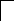
Розглянемо обчислювання елементів другої матриці за правилом „прямокутників”:

Викреслюємо третій стовпчик (оскільки він пропорційний першому) і переходимо до наступного кроку.

, оскільки ранг матриці не може перевищувати мінімального із кількості рядків та стовпців матриці. В результаті еквівалентних елементарних перетворень дістали трикутну матрицю 2–го порядку із відмінними від нуля діагональними елементами. Значить .

Завдання для розв’язування.

Обчислити ранг матриці:

а) ;

б) ;

ТЕМА 4: Розв’язування систем лінійних рівнянь зневідомими за допомогою оберненої матриці та за правилом Крамера. Дослідження та розв’язування системлінійних рівнянь зневідомими.

Розв’язування систем лінійних рівнянь зневідомими за допомогою оберненої матриці та за правилом Крамера.

Розглянемо систему лінійних алгебраїчних рівнянь (СЛАР) з невідомими:

(*).

Означення . Розв’язком СЛАР (*) називається упорядкована множина дійсних чисел, яка при підстановці у систему замість невідомих перетворює її в систему тотожностей (систему правильних числових рівностей).

Матричний метод

Позначимо:

, ,.

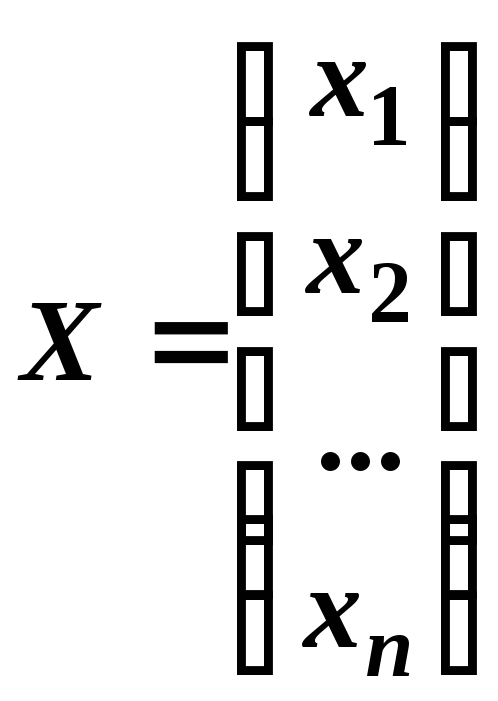Тут: – матриця коефіцієнтів при невідомих (основна матриця системи);

–матриця-стовпець невідомих;

–матриця-стовпець вільних членів (правих частин).

Тоді СЛАР (*) можна записати у вигляді матричного рівняння:

.

Якщо , то існує. Домножимо обидві частини матричного рівняння зліва на. Одержимо:

,

,

.

Отже, справедлива наступна

Теорема. Якщо визначник основної матриці СЛАР (*) відмінний від нуля, то система має єдиний розв’язок, який знаходиться як добуток оберненої доматриціна матрицю–стовпець вільних членів.

Приклад. Розв’язати за допомогою оберненої матриці СЛАР:

.

Розв’язування.

1. Позначимо:

–матриця коефіцієнтів при невідомих;

–матриця-стовпець невідомих;

–матриця-стовпець вільних членів.

2. Запишемо систему у вигляді матричного рівняння .

3. Обчислимо :система має єдиний розв’язок. Оскільки, то існує обернена матриця .

Знайдемо її:

Отже, .

Таким чином,

.

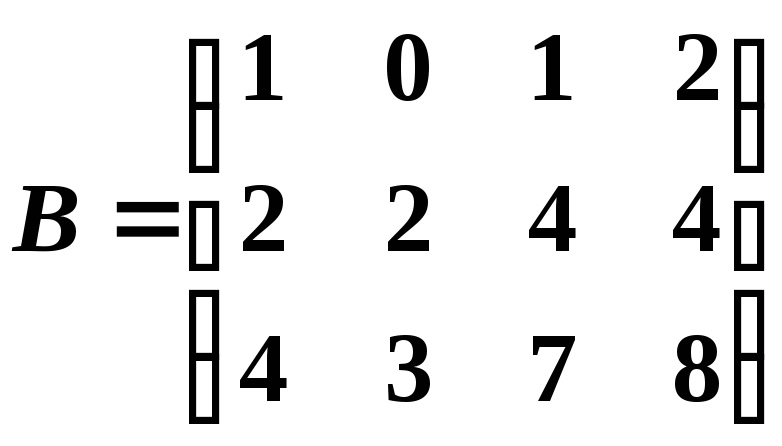
Відповідь: ,.