Похідна неявної функції, логарифмічне диференціювання.

Нехай значення змінних зв’язані між собою рівнянням. Якщо функціявизначена на деякій множині і при підстановці у рівнянняперетворює його в тотожність, то кажуть, щофункція задана неявно і записують .

Відзначимо, що будь-яку явно задану функцію можна записати у неявному вигляді .

При диференціюванні неявної функції потрібно користуватись теоремою про похідну складеної функції, враховуючи, що є функцією аргумента . В якості приклада розглянемо так званелогарифмічне диференціювання, яке застосовується для знаходження похідної степенево-показникової функції .

Знайти похідну функції .

Проблемою тут є те, що незрозуміло, яку із функцій вважати зовнішньою: степеневу чи показникову. Тому, спочатку логарифмують (як правило, за натуральною основою) обидві частини рівності (при ):

.

Отримали неявну функцію, яку диференціюємо:

.

Звідси .

Зауважимо, що логарифмічне диференціювання часто застосовують і при економіко-математичному моделюванні.

Диференціал. Геометричний сенс, інваріантність форми диференціалу. Похідні та диференціали вищих порядків.

Розглянемо функцію , яка визначена в околі точкиі має похідну в точці, тобто існує границя. Звідси, за теоремою про зв’язок збіжної та нескінченно малої:

або , де- НМ при.

Означення. Диференціалом функції в даній точці називається головна, лінійна відносно, частина приросту функції в цій точці. Для функції, яка має похідну, диференціал дорівнює добутку похідної функціїв точціна довільний приріст аргументу в цій точці.

Позначається: .

Наслідок. Якщо , то, тобто диференціал незалежної змінної дорівнює довільному приросту цієї змінної. Тому. Це дозволяє сприймати записне тільки як позначення похідної, а і як відношення диференціалів (що часто використовується).

Основні властивості диференціала.

1. ,де

2.

3.

4.

5.

Наприклад, знайти диференціал функції:

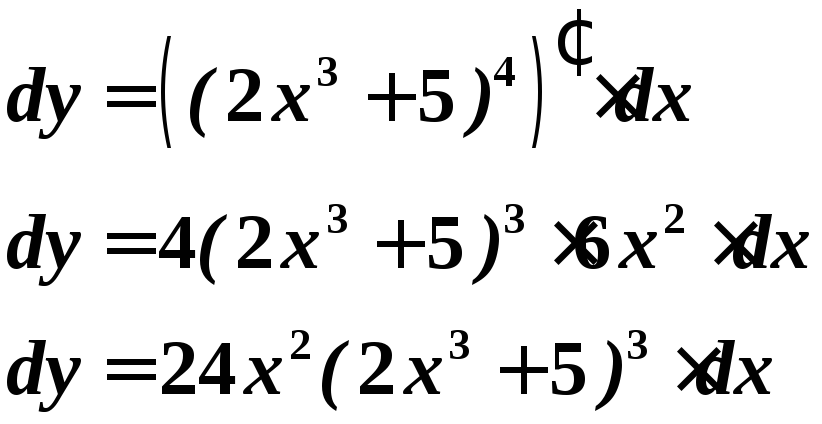
Н

у

ехай функціядиференційовна в точці. Тоді в точціграфік функції має дотичну, що утворює кут,із додатним напрямом осі:

М В М0 А α х

Із рисунка видно, що , тобто диференціал функції в точці дорівнює приросту дотичної до кривоїв точці, коли незалежна змінна дістає приріст. Це єгеометричний зміст диференціала функції.

Аналізуючи рисунок, можна помітити, що , тобто, має місце наближена рівність, і вона тим точніша, чим менше приріст аргумента.

Таким чином, при досить малому можна записати наближену рівність:

.

Цю формулу часто використовують при наближених обчисленнях.

Нехай складена функція визначена на множині. Знайдемо її диференціал:

.

Ця формула виражає інваріантність форми диференціалу першого порядку. Вона стверджує, що диференціал складеної функції дорівнює добутку похідної зовнішньої функції на диференціал її аргумента (внутрішньої функції). Але на відміну від звичайної функції, у цій формулі не можна замінити диференціал на приріст(оскільки це функція, а не аргумент).

Нехай функція диференційовна на деякій множині, а- її похідна, яка, в свою чергу, є функцією аргумента. Для цієї функціїможна визначитипохідну другого порядку, якщо вона існує:

.

Означення. Похідною –го порядку називається похідна від похідної –го порядку і позначається , тобто

Приклад.

Знайти похідні вищих порядків для функції

Розв’язування:

; ;;;.

Зауваження. Похідні –го та більш високих порядків від многочленів –го степеня тотожньо дорівнюють нулю.

Аналогічно визначаються диференціали вищих порядків. Наприклад, диференціал другого порядку:

.

ТЕМА 15: Теорема Лагранжа, наслідки. Теорема Коші, правило Лопіталя. Критерій монотонності, наслідок. Екстремум функції. Необхідна умова екстремума. Перша достатня умова екстремума. Дослідження функцій на монотонність та екстремуми. Опуклість, угнутість, точки перегину. Друга достатня умова екстремума. Асимптоти. Повне дослідження функції.

Теорема Лагранжа, наслідки. Теорема Коші, правило Лопіталя.

Теорема (Лагранжа). Нехай функція неперервна на сегментіі диференційовна на інтервалі. Тоді існує хоча б одна точкатака, що:

.

Геометрично:

Тобто, на графіку функції існує точка з абсцисою , в якій дотична паралельна хорді.

Із теореми безпосередньо випливає так звана формула Лагранжа (формула скінчених приростів):

.

Наслідок 1. Нехай функція неперервна на сегментіі диференційовна на інтервалі. Якщо похідна функції тотожньо дорівнює нулю, тобто, то функція на цьому відрізку є сталою.

Доведення.

Наслідок 2. Для того, щоб диференційовні на деякому проміжку функції імали тотожно рівні похідні необхідно і достатньо, щоб ці функції відрізнялись лише на сталу величину, тобто:

.

Доведення.

Теорема (Коші). Нехай функції неперервні на сегментіі диференційовні на інтервалі, причому. Тоді існує хоча б одна точкатака, що:

.

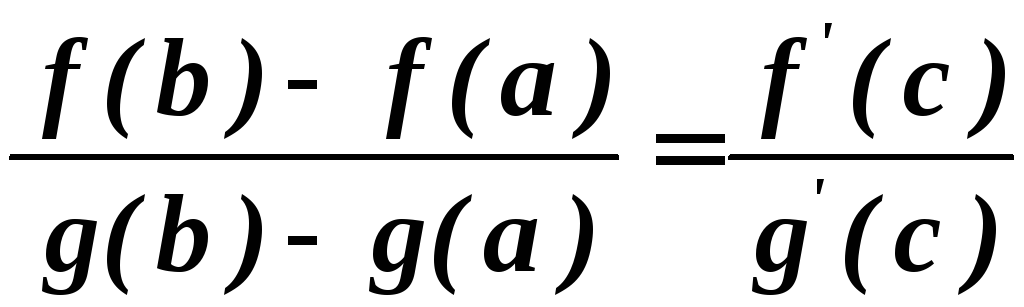Використовуючи теорему Коші, можна довести правило Лопіталя.

Нехай функції ідиференційовні в околі точки(або при). Тоді:

.

Приклад. Знайти границю:

за правилом Лопіталя