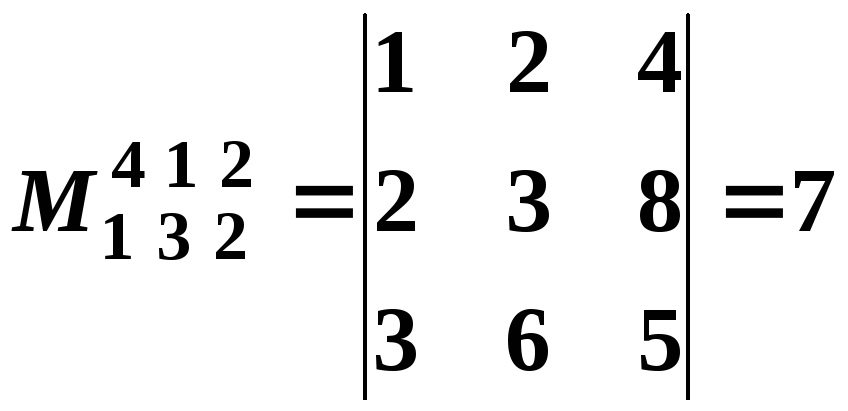- •Міністерство освіти і науки, молоді та спорту україни
- •Розділ і. Лінійна алгебра
- •Тема 1: Матриці. Різновиди матриць. Операції над матрицями. Матриці та їх різновиди.
- •Операції над матрицями.
- •Завдання для розв’язування.
- •Тема 2: Визначники, правила їх обчислення. Властивості визначників. Обернена матриця. Визначники, правила їх обчислення.
- •Властивості визначників.
- •Завдання для розв’язування.
- •Обернена матриця.
- •Тема 3: Ранг матриці. Знаходження рангу матриці.
- •Методом елементарних перетворень.
- •Завдання для розв’язування.
- •Матричний метод
- •Метод Крамера.
- •Завдання для розв’язування.
- •Дослідження та розв’язування систем лінійних рівнянь з невідомими.
- •Розв’язування систем m лінійних рівнянь з n невідомими методом Жордана-Гаусса.
- •Тема 5: Лінійний векторний простір. Лінійно залежні та лінійно незалежні векторні системи, їх властивості. Базис. Розклад за базисом. Лінійний векторний простір.
- •Лінійно залежні та лінійно незалежні векторні системи, їх властивості.
- •Властивості лз векторних систем.
- •Властивості лнз векторних систем.
- •Зауваження. Розділ іі. Аналітична геометрія
- •Тема 6: Метод координат. Елементи векторної алгебри. Найпростіші задачі аналітичної геометрії.
- •Метод координат.
- •Елементи векторної алгебри.
- •Основні означення.
- •Операції над векторами.
- •Умова колінеарності.
- •Скалярний добуток.
- •3. Вектори і перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю, тобто
- •Завдання для розв’язування.
- •Найпростіші задачі аналітичної геометрії.
- •Завдання для розв’язування
- •Тема 7: Рівняння лінії. Основне означення аналітичної геометрії. Пряма на площині. Рівняння лінії.
- •Пряма лінія.
- •Дослідження загального рівняння прямої
- •Рівняння прямої, що проходить через дану точку паралельно даному вектору (канонічне рівняння прямої).
- •Рівняння прямої, що проходить через дві задані точки.
- •Рівняння прямої у відрізках на осях.
- •Відстань від точки до прямої.
- •Кутовий коефіцієнт прямої. Рівняння прямої з кутовим коефіцієнтом.
- •Взаємне розташування двох прямих. Умова паралельності та перпендикулярності прямих.
- •Тема 8: Перетворення системи координат.
- •Паралельне перенесення
- •2. Поворот координатних осей
- •Тема 9: Криві іі порядку.
- •Характеристична властивість точок еліпса
- •Характеристична властивість точок м(х; у) гіперболи.
- •Рівнобічна гіпербола.
- •Характеристична властивість точок параболи (геометричне означення параболи).
- •Завдання для розв’язування.
- •Тема 10: Застосування методів лінійної алгебри та аналітичної геометрії до розв’язування деяких економічних задач.
- •Розділ ііі. Вступ до аналізу
- •Тема 11: Функції. Основні поняття. Послідовності. Границя послідовності. Властивості границі. Функції. Основні поняття.
- •Послідовності.
- •Властивості границі.
- •Властивості нм
- •Арифметичні теореми для збіжних послідовностей.
- •Теореми порівняння.
- •Розкриття невизначеностей.
- •Неперервність функції.
- •Класифікація точок розриву.
- •Властивості функцій, неперервних на замкненому проміжку.
- •Розділ іу. Диференціальне числення
- •Арифметичні теореми. Похідна складеної, оберненої функції. Таблиця похідних основних елементарних функцій. Логарифмічне диференціювання, похідна неявної функції.
- •Похідна неявної функції, логарифмічне диференціювання.
- •Диференціал. Геометричний сенс, інваріантність форми диференціалу. Похідні та диференціали вищих порядків.
- •Основні властивості диференціала.
- •Критерій монотонності, наслідок. Екстремум функції. Необхідна умова екстремума. Перша достатня умова екстремума. Дослідження функцій на монотонність та екстремуми.
- •Опуклість, угнутість, точки перегину. Друга достатня умова екстремума. Асимптоти. Повне дослідження функції.
- •Тема 16: Застосування методів диференціального числення до розв’язування деяких економічних задач.
- •Практичне заняття №1
- •Практичне заняття №4
- •Практичне заняття №6
- •Практичне заняття №8
- •1. Криві другого порядку, їх класифікація.
- •2. Дослідження кривих (зведення до нормальних рівнянь). Основні параметри кривих та їх схематична побудова.
- •Практичне заняття №8
- •Практичне заняття №11
- •Практичне заняття №13
- •Практичне заняття №14 контрольна робота з техніки диференціювання практичне заняття №15
- •Практичне заняття №16
- •Практичне заняття №17
- •Практичне заняття №18
Завдання для розв’язування.
Обчислити визначники:
|
а) |
б)
|
в)
|
г) |
д) |
|
ж)
|
з)
|
е)
|
Обернена матриця.
Повернемось до операції «ділення матриць» (яку визначимо як добуток на обернену матрицю).
Нехай
 – квадратна матриця порядку
– квадратна матриця порядку
![]() .
.
Означення.
Матриця
![]() називається
оберненою
до матриці
називається
оберненою
до матриці
![]() ,
якщо
,
якщо
![]() -
одинична матриця.
-
одинична матриця.
Зауваження.
Очевидно,
що
![]() – квадратна матриця того ж порядку, що
і
– квадратна матриця того ж порядку, що
і
![]() .
.
Означення.
Квадратна матриця
![]() називаєтьсяневиродженою,
якщо її визначник
називаєтьсяневиродженою,
якщо її визначник
![]() .
У супротивному випадку матриця
.
У супротивному випадку матриця![]() називаєтьсявиродженою.
називаєтьсявиродженою.
Справедлива наступна
Теорема.
Для існування оберненої матриці
![]() до квадратної матриці
до квадратної матриці![]() необхідно і достатньо, щоб її визначник
необхідно і достатньо, щоб її визначник![]() (тобто матриця
(тобто матриця![]() повинна
бути невиродженою).
повинна
бути невиродженою).
Доведення.
Схема знаходження оберненої матриці.
Знаходимо визначник матриці
 .
Якщо
.
Якщо ,
якщо ж
,
якщо ж - вироджена, і
- вироджена, і не
не
 .
.Знаходимо
 –
алгебраїчні доповнення усіх елементів
–
алгебраїчні доповнення усіх елементів
 визначника.
визначника.
Записуємо обернену матрицю:
 .
.
Якщо потрібно, виконуємо перевірку:
![]() (або
(або
![]() ).
).
Наприклад, знайти обернену для матриці
 .
.
Розв’язування.
![]()
![]()
Тема 3: Ранг матриці. Знаходження рангу матриці.
Розглянемо
матрицю розміру
![]() .
.
 .
.
Означення.
Мінором
![]() -го
порядку
-го
порядку
![]() матриці
матриці
![]() називається визначник
називається визначник
![]() -го
порядку, складений з елементів матриці,
які розташовані на перетині деяких
-го
порядку, складений з елементів матриці,
які розташовані на перетині деяких
![]() рядків і
рядків і
![]() стовпців.
стовпців.
Наприклад:
 ,
,
![]() ,
,
![]() –
мінори 1–го порядку. Очевидно, що мінорами
1–го порядку є елементи матриці.
–
мінори 1–го порядку. Очевидно, що мінорами
1–го порядку є елементи матриці.
|
|
– мінор 2–го порядку. (В мінорах матриці нижні індекси вказують номери рядків, а верхні – номери стовпців матриці, які використовуються для утворення даного мінора). |
|
|
|
– мінори 3–го порядку |
|
|
– мінор 4–го порядку, який містить нульовий рядок. |
Приклад
дозволяє зробити такий висновок: для
ненульової матриці
![]() можливий порядок
можливий порядок![]() її мінорів – це натуральне число, яке
задовольняє нерівність
її мінорів – це натуральне число, яке
задовольняє нерівність![]() .
.
Означення. Рангом матриці називається максимальний порядок її відмінного від нуля мінора. Ранг нульової матриці дорівнює нулю.
Ранг
матриці
![]() позначається
позначається![]() і, очевидно, задовольняє нерівність
і, очевидно, задовольняє нерівність![]() .
.
У
розглянутому прикладі у матриці
![]() є відмінний від нуля мінор 3–го порядку,
а всі мінори 4-го порядку дорівнюють
нулю (переконайтесь самостійно). За
означенням,
є відмінний від нуля мінор 3–го порядку,
а всі мінори 4-го порядку дорівнюють
нулю (переконайтесь самостійно). За
означенням,![]() .
.
Приклад 1.
![]() ,
,
![]() ,
а всі мінори 2–го порядку дорівнюють
нулю (перевірте самостійно, враховуючи
властивості визначників). Тому
,
а всі мінори 2–го порядку дорівнюють
нулю (перевірте самостійно, враховуючи
властивості визначників). Тому
![]() .
.
Приклад 2.
 ;
;
![]() ;
;![]() .
.
 .
Отже,
.
Отже,
![]() .
.
Таким
чином, якщо
![]() ,
то це означає, що у даної матриці
,
то це означає, що у даної матриці![]() є мінор порядку
є мінор порядку![]() ,
відмінний від нуля, а всі мінори більш
високих порядків (якщо вони існують)
дорівнюють нулю.
,
відмінний від нуля, а всі мінори більш
високих порядків (якщо вони існують)
дорівнюють нулю.
Приклад 3.
 –одинична
матриця
–одинична
матриця
![]() -го
порядку.
-го
порядку.
![]() ,
тобто ранг одиничної матриці дорівнює
її порядку.
,
тобто ранг одиничної матриці дорівнює
її порядку.
Важливе зауваження: ранг діагональної, трикутної (верхньої або нижньої) матриці, діагональні елементи якої відмінні від нуля, дорівнює її порядку (тобто, кількості цих відмінних від нуля діагональних елементів).
Означення. Елементарними перетвореннями матриці називаються такі операції над матрицею:
Транспонування матриці.
Перестановка місцями паралельних рядів.
Викреслювання нульового ряду, а також усіх, окрім одного, із паралельних пропорційних рядів.
Множення ряду на число, відмінне від нуля.
Додавання до елементів ряду відповідних елементів паралельного ряду, помножених на довільне число.
Неважко переконатись, що справедлива наступна
Теорема. Елементарні перетворення не змінюють рангу матриці.
Означення. Матриці називаються еквівалентними, якщо вони мають однаковий ранг.
За допомогою елементарних перетворень довільну ненульову матрицю можна привести до еквівалентної їй трикутної матриці, діагональні елементи якої відмінні від нуля. На цьому базується метод знаходження рангу матриці.
Схема обчислення рангу матриці




 ;
; ;
; .
. ,
,