Manzhosov2

Тогда

H T П 12 m r2 r2 2 kmr .

Находим обобщенные импульсы pr и pφ:

p

r

L

H

mr ;

p

L

H

mr 2 .

r

r

Отсюда

p

r

p

r

,

.

mr2

m

Функция Гамильтона Н в канонических переменных принимает вид

1

2

H

p2

p

km .

2m

r

r

2

r

Канонические уравнения будут следующими:

dr

H

p

r

,

dp

r

H

p2

mk

,

dt

pr

m

dt

r

r3

r 2

d

H

p

,

dp

H

0 .

dt

p

mr 2

dt

Эти уравнения определяют r, φ, pr и pφ в функции t.

Из последнего уравнения находим

p

, где const .

Подставляем это значение в уравнение d

или

r 2 d

,

mr 2

m

что является уравнением площадей.

dt

dt

Аналогично находим pr

m dr .

dt

Тогда

dp

r m

d 2 r

2

mk

,

dt 2

r

r 2

dt

2

или

d

2 r

2

k

.

dt 2

mr

2

r 2

Приведенное выражение есть дифференциальное уравнение, определяющее движение материальной точки по радиусу.

Пример 2. Определить уравнения движения точек свободной механической системы, движущейся по инерции.

Решение. Для свободной механической системы, движущейся по инерции, функция Лагранжа имеет следующее выражение:

L T 1 mi ki2	yi2 zi2 .
n
i 1 2

Так как декартовы координаты точек системы не входят явно в выражение функции Лагранжа, то все они являются циклическими координатами.

В этом случае все обобщенные импульсы постоянны: 101

pxi	L	mi xi i ,	pyi	L	mi
	xi			yi

Функция Гамильтона принимает вид

n

H L

i 1

Тогда

dxi H i ; dyi dt i mi dt

yi	i ,	pzi	L	mi zi	i i (1, 2, ..., n).
			zi

2m1 i i2 i2 i2 .

	H		i	;	dzi	H	i	.
			mi
	i				dt	i	mi

Уравнения движения точек системы в декартовых координатах имеют вид

x

i

i

t a

i

;

y

i

i

t b ;

z

i

i

t c

i

i (1, 2, ..., n).

mi

mi

i

mi

Как видно, координаты всех точек системы линейно зависят от времени.

Основные свойства скобок Пуассона. Теорема Пуассона

Для установления основных свойств скобок Пуассона предположим, что заданы две функции φ и ψ, явно зависящие от времени t и канонических переменных qj и pj (j=1, 2, …, s):

φ= φ(q1, q2, …, qs, p1, p2, …, ps, t),

ψ= ψ(q1, q2, …, qs, p1, p2, …, ps, t).

Скобки Пуассона для этих функций имеют вид

	,								.
	q j p j					p j q j

К числу основных свойств скобок Пуассона относятся следующие: 1. При перестановке функций знак у скобок Пуассона изменяется:

(φ, ψ) = –(ψ, φ).

2. Если одна из функций – постоянная величина, то скобки Пуассона равны нулю:

(φ, С) = 0.

3. Частная производная по времени t от скобок Пуассона определяется следующим вы-

ражением:
,
t		t	,	,	t	.

4. Скобки Пуассона для функций φ = φ1 + φ2 и ψ определяются следующим выражением:

(φ1+φ2, ψ) =(φ1, ψ)+(φ2, ψ).

5. Если заданы три произвольные функции f, φ и ψ, зависящие от времени t и канонических переменных qj и pj (j = 1, 2, ..., s), то между скобками Пуассона, составленными для этих трех функций, взятых попарно, выполняется следующее тождество:

f ,( , ) ,( , f ) ,( f , ) 0 .

102

Это тождество называется тождеством Якоби – Пуассона.

Теорема Пуассона: если известны два интеграла системы канонических уравнений динамики

φ (q1, q2, …, qs, p1, p2, …, ps, t) = a; ψ (q1, q2, …, qs, p1, p2, …, ps, t) = b,

то функция (φ, ψ) является также одним из интегралов канонических уравнений. Основываясь на теореме Пуассона, можно было бы считать, что по двум известным

первым интегралам канонических уравнений можно последовательно найти все 2s первых интегралов этих уравнений. В действительности найти общее решение системы канонических уравнений с помощью этой теоремы не всегда удается.

Причиной этого является то, что скобки Пуассона от двух интегралов могут дать один из первых интегралов, найденных уже ранее, или они могут оказаться тождественно равными нулю.

Метод Остроградского–Якоби. Применение метода Остроградского–Якоби в случае, когда функция Гамильтона Н явно от времени не зависит.

Примеры применения метода Остроградского–Якоби

Метод Остроградского–Якоби позволяет свести задачу об отыскании 2s первых интегралов дифференциальных уравнений канонической системы к задаче определения полного интеграла некоторого уравнения в частных производных первого порядка.

Заменим в выражении функции Гамильтона H все обобщенные импульсы p1, р2, ..., рs частными производными первого порядка от некоторой неизвестной функции S и составим уравнение в частных производных следующего вида:

S

S

S

S

, q2

,..., qs ,

,

,...,

0 .

t

q

q

q

H t, q1

2

1

s

Это уравнение называется уравнением Остроградского–Якоби.

Уравнение представляет собой линейное дифференциальное уравнение в частных производных первого порядка относительно неизвестной функции S, зависящей от s + 1 переменных t, ql, q2, ..., qs.

Неизвестная функция S, удовлетворяющая уравнению Остроградского–Якоби,

называется производящей функцией.

Так как функция S явно не входит в уравнение, то общий интеграл этого уравнения имеет вид

S S * t, q1 , q2 ,..., qs , 1 , 2 ,..., s s 1 ,

где S* – полный интеграл уравнения Остроградского–Якоби.

Постоянная αs+1 является аддитивной, т. е. входит в общий интеграл в качестве слагаемого.

Теорема Остроградского–Якоби, на которой основывается предложенный ими метод, формулируется так: если известен полный интеграл уравнения Остроградского–Якоби, то 2s независимых интегралов канонической системы уравнений имеют следующий вид:

S *		(k = 1, 2, …, s);
	k
k
S *		(k = 1, 2, …, s).
	pk
qk
		103

Соотношения показывают, что интегралы канонической системы уравнений получаются дифференцированием полного интеграла по обобщенным координатам и произвольным постоянным.

Из теоремы Остроградского–Якоби следует, что в том случае, если известен полный интеграл уравнения Остроградского–Якоби, переменные qj и pj определяются как функции времени t и 2s произвольных постоянных α1, α2, …, αs, β1, β2, …, βs из уравнений, представляющих собой по отношению к qj и pj систему алгебраических уравнений.

В случае, если функция Гамильтона Н явно от времени не зависит, уравнение Остроградского–Якоби имеет вид

S

S

S

S

,q2

,...,qs ,

,

,...,

0.

t

q

q

q

H q1

2

1

s

Так как время t не входит явно в это уравнение, то число независимых переменных в этом случае уменьшается на единицу, т. е. равно 2s.

Полагая, что

S * W q1 , q2 ,..., qs ht ,

где W – новая неизвестная функция, называемая характеристической функцией, зависящая только от обобщенных координат q1, q2, ..., qs, a h – постоянная. Тогда

S

h ,

p

k

S

W

(k = 1, 2, …, s).

t

qk

qk

Получаем уравнение Остроградского–Якоби для определения W, не содержащее

времени t:

W

W

W

,q2

,...,qs ,

,...,

h T П.

H q1

q ,

q

2

q

s

1

Общий интеграл зависит от s + 1 постоянных α1, α2, …, αs, h, одна из которых αs входит как аддитивная постоянная, так как функция W не входит явно в уравнение. Из этого следует, что функция W определяется с точностью до аддитивной постоянной.

Таким образом, общий интеграл уравнения имеет вид

W W * q1 ,q2 ,...,qs , 1 , 2 ,..., s 1 ,h , s .

Тогда

S ht W * q1 ,q2 ,...,qs , 1 , 2 ,..., s 1 ,h s .

Теперь на основании теоремы Остроградского–Якоби, пользуясь формулами, можно составить полную систему независимых интегралов канонических уравнений движения:

S *		W *	(k = 1, 2, …, s–1).
		k
k		k

Интегралы не содержат в явном виде времени t и называются геометрическими. Эти уравнения в многомерном пространстве обобщенных координат определяют кривую – траекторию изображающей точки.

S *	W	*	(k = 1, 2, …, s).
	qk	pk
qk
		104

Интегралы служат для определения импульса, а также постоянных интегрирования.

S *	t	W	*	W	*
h		h	t0 или	h	t t0 ,

где t0 – произвольная постоянная, которую можно принять в качестве начала отсчета времени.

Интеграл, содержащий время, называется кинетическим и определяет движение изображающей точки по траектории.

Пример 1. Свободная материальная точка массой m движется по прямой линии под действием силы притяжения к центру О, расположенному на этой прямой. Сила притяжения пропорциональна расстоянию от точки до этого центра.

Найти канонические уравнения движения материальной точки и уравнение ее движения, применив метод интегрирования Остроградского–Якоби.

Решение. Свободная материальная точка, движущаяся по прямой, имеет одну степень свободы. Примем эту прямую за ось координат Oq, поместив начало координат в центре притяжения. Тогда расстояние от точки притяжения q будет ее обобщенной координатой.

Так как сила притяжения пропорциональна расстоянию q от точки до центра

	притяжения, а коэффициент пропорциональности равен с, то потенциальная энергия
	материальной точки П cqdq	cq2	.
	2
	Кинетическая энергия материальной точки T					mq			2	.
						2
	Вычислим функцию Лагранжа: L T			П	mq2			cq			2
											.
					2				2			p
	Находим обобщенный импульс: p L
				mq , откуда q									.
			q									m

Функция Гамильтона, выраженная в канонических переменных, имеет вид

H T П p2 cq2 h . 2m 2

Находим канонические уравнения движения точки:

	dq		H		p	,	dp		H	cq .
	dt		p		m		dt		q

Как видно, функция Н не зависит явно от времени. Составим уравнение для определения характеристической функции W.

										2	2
						1		W		cq
	Имеем										h.
								q
						2m				2
	Тогда	W		2mh mcq2	и W *			2mh mcq2 dq.
		q

Полный интеграл будет иметь следующий вид:

S * ht

2mh mcq2 dq.

Из интегралов канонических уравнений движения находим выражение для импульса: 105

p S * q 2mh mcq2 .

Уравнение движения точки на основании (к) выразится так:

S *h

Приводим его к виду t 1

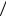где A2 2hc и 2 cm .

Так как

	t		mdq	t0 .
			2mh mcq2

	dq		t0	,
	A2	q2

		dq		arcsin	q	,
	A	2	2		A
		q

то уравнение движения точки получается в следующем виде: q Asin t t0 , или q Asin t ,

где β = ωt0.

Пример 2. Материальная точка массой m движется под действием силы притяжения к некоторому центру О. Зная, что силовая функция поля равна U(r), где r – расстояние от точки до центра О, найти канонические уравнения и уравнения ее движения, применив метод интегрирования Остроградского–Якоби.

Решение. Выберем за обобщенные координаты материальной точки ее полярные координаты r и φ. Так как составляющие скорости точки, выраженные в полярных координатах, определяются по формулам

vr r и v r , то v r 2 r 2 2 .

Тогда кинетическая энергия материальной точки

T 12 m r2 r2 2 .

Находим выражение функции Лагранжа:

L T U 12 m r2 r2 2 U r .

Вычислим обобщенные импульсы:

p

r

L

mr ,

p

L

mr2 .

r

Отсюда

r

p

r

,

p

.

m

mr

2

Функция Гамильтона для рассматриваемого движения материальной точки имеет вид

	1				2
H		p2			p		U r .
	2m		r		r 2
			106

Для определения характеристической функции W применим уравнение в виде

	1		W		2	1		W	2
h										U r 0.
	2		r
						r 2

В это уравнение угол φ явно не входит, а потому полный интеграл уравнения будем искать в виде

W * f r .

Необходимо, чтобы функция f(r) удовлетворяла дифференциальному уравнению

	1		f	2		2
h							U r 0.
	2		r		r 2

Отсюда

f r 2 U h r 22 dr .

Тогда полный интеграл уравнения Остроградского–Якоби имеет вид

W *	2 U h 2 r 2 dr.

Уравнения движения материальной точки будут следующими:

W *

dr

;

r

2

2 U h

2

r

2

W

*

dr

t t0 .

h

2 U h 2 r 2

Первое уравнение определяет траекторию, а второе – время, необходимое для достижения точкой заданного положения на этой траектории.

Пример 3. Материальная точка массой m движется в однородном поле силы тяжести. Найти методом Остроградского–Якоби траекторию точки и уравнение ее движения.

Решение. Выберем за обобщенные координаты материальной точки ее декартовы координаты х, у, z. Ось z направим вертикально вверх. Тогда выражения кинетической энергии точки, ее потенциальной энергии и кинетического потенциала будут следующими:

T 12 m x2 y2 z2 ; П mgz ; L T П 12 m x2 y2 z2 mgz .

Находим выражения для обобщенных импульсов:

px

L

mx

, py

L

my

,

pz

L

mz ,

x

y

z

откуда

x

p

x

, y

py

, z

p

z

.

m

m

m

107

Функция Гамильтона получает следующий вид:

H T П 12 m px2 py2 pz2 mgz h .

Для определения характеристической функции W заменим в этом выражении обобщенные импульсы частными производными от характеристической функции по соответствующим координатам и получим следующее уравнение Остроградского–Якоби:

	W 2		W 2		W 2		2m	2	gz 2mh .
					z
	x		y

Так как координаты х и у не входят явно в выражение функции Н, то они являются циклическими координатами. Поэтому положим, что

W* = αx +βy + f(z).

Вычислим частные производные от W и подставим их в уравнение:

2 2 f 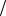z 2 2m2 gz 2mh .

Из этого уравнения находим

f 2mh 2 2 2m2 gz .z

Интегрируем это уравнение с точностью до аддитивной постоянной: f z, , , h 3m12 g 2mh 2 2 2m2 gz 3 .

Тогда характеристическая функция примет вид

W x y f z, , , h C .

Получаем следующие интегралы движения материальной точки:

	W	*	f		W	*	f		W *
		x		d ;		y		b ;	h

Вявном виде эти уравнения будут следующими:

x m2 g F z, , , h d ,

y m2 g F z, , , h e ,1 mg F z, , , h t t0 ,

где F z, , , h 2mh 2 2 2m2 gz .

f t t0 .h

Первые два интеграла в этой системе геометрические, представляющие собой уравнения цилиндрических поверхностей, пересечение которых представляет собой траекторию точки.

Уравнение этой траектории таково:

x d y b .

Этиуравненияпоказывают, чтотраекторияточкинаходитсявплоскости, параллельнойосиz. 108

Если с этой плоскостью совместить плоскость Охz, то у = 0 и β= 0. В этом случае первое из уравнений можно представить в виде

	x d 2	2	2mh 2 2m2 gz .
		m4 g 2

Это естьуравнение параболы, расположеннойв плоскости Охz с осью, параллельной оси z. Третий интеграл системы кинематический, он устанавливает уравнение движения

точки в виде

2mh 2 2 2m2 gz t t0 2 , m2 g 2

Откуда z	2mh 2 2		g	t t0 2 .
	2m2 g
		2

Постоянные α, β, d, е, h, t0 определяются заданием начальных условий движения, т. е. начального положения точки (три координаты) и начальной скорости (три ее проекции).

Для определения этих постоянных составляются еще три интеграла:

W *	px ;	W *	py ;	W *	pz F z, , , h .
x		y		z

Все шесть постоянных интегрирования определяются по начальным условиям движения.

Таким образом, применение канонических уравнений механики позволяет получать результаты решения задач, обладающие большой общностью.

1.2.5. Вариационные интегральные принципы классической механики

Общие понятия

Вариационными принципами классической механики называют общие закономерности механического движения, позволяющие из совокупности кинематически возможных движений механической системы, т. е. движений, допускаемых наложенными на систему связями, выделить действительное движение, которое она будет совершать в заданном силовом поле.

Вариационные принципы разделяются на дифференциальные и интегральные. Дифференциальные вариационные принципы дают критерий истинного движения, отнесенный к некоторому моменту времени, а интегральные – к конечному интервалу времени.

Важнейшим и наиболее общим дифференциальным вариационным принципом классической механики является принцип возможных перемещений.

Важнейшими интегральными принципами классической механики являются принцип Гамильтона–Остроградского и принцип стационарного действия Мопертюи–Лагранжа.

Положение голономной механической системы с s степенями свободы относительно системы отсчета определяется обобщенными координатами (q1, q2, …, qs), которые при движении механической системы изменяются, являясь функциями времени t.

Совокупность обобщенных координат механической системы (q1, q2, …, qs) для каждого момента времени можно рассматривать как координаты точки в пространстве s измерений. Тогда каждой конфигурации механической системы, т. е. ее положению в

109

пространстве, будет соответствовать определенная точка в s-мерном пространстве. Условимся называть s-мерное пространство пространством конфигураций.

С течением времени положение системы в пространстве изменяется, и точка, изображающая эту систему, описывает в пространстве конфигураций некоторую кривую. Условимся называть эту кривую траекторией движения системы. Движение изображающей точки вдоль этой траектории отображает действительное движение системы в пространстве.

Очевидно, что каждой точке такой траектории в пространстве конфигураций соответствует определенное положение механической системы в реальном евклидовом пространстве.

Отбор действительного движения механической системы из совокупности ее возможных движений можно осуществить с помощью анализа ее движения в пространстве конфигураций на основе интегральных вариационных принципов, изложенных ниже.

Дифференцирование и варьирование в механике

Предположим, что механическая система имеет одну степень свободы и ее положение определяется обобщенной координатой q = f(t).

Дифференцируем это равенство по времени: dq f (t)dt .

Дифференциал обобщенной координаты dq соответствует ее изменению вследствие изменения времени, т. е. вследствие действительного движения системы.

Геометрически dq есть отрезок a1b1 (рис. 2.24), но с точностью до бесконечно малых высшего порядка dq равен отрезку a1c1. Дадим функции q = f(t) при заданном зафиксированном значении аргумента t произвольное приращение δq:

q (t) ,

где ε – произвольно малое постоянное число, а φ(t) – произвольная дифференцируемая функция времени.

Рис. 2.24	Рис. 2.25
Получим семейство новых функций времени:
	q f (t) (t) .
	~
Графически одна из функций	q представлена новой кривой, бесконечно близкой к
	~

кривой функции q (рис. 2.25).

Произвольное изменение функции δq, являющееся следствием не изменения аргумента, а изменения вида самой функции, называется синхронной вариацией функции:

q q~ q (t) .

Вариация функции δq в момент t (рис. 2.25) соответствует отрезку ае. Рассмотреннаяоперацияварьированияфункцииназываетсясинхроннымварьированием.

110