Manzhosov2

Значение коэффициента k можно определить по условию, что при x0 = 5 см сила

отталкивания Р0 = 0,4 мH = 40 дин: k = 5000 г·см4/с2.

Составим дифференциальное уравнение движения точки М: m x =ΣXi=P = k/x3;

Преобразовав и разделив переменные, получим: mv·dv=(k/x3)·dx.

При интегрировании уравнения воспользуемся определенными интегралами с переменным верхним пределом. При изменении скорости от v0 до v координата точки

изменяется от х0 до х. Тогда, преобразовав, получим: mv2/2 – mv02/2 = k/2(1/x02 – 1/x2).

Подставив числовые значения k, m, v0, получим v = (110 – 250/x2)1/2.

Полученное выражение определяет скорость v точки в зависимости от ее координаты х.

Из этого уравнения можно найти искомое значение скорости при х = 20 см: v = (10,46)1/2 см/с.

Заменим v = dx/dt и, разделив переменные, проинтегрируем левую часть в пределах от xо = 5 до x, а правую – в пределах от t0 = 0 до t и, преобразовав, получим:

x2 – 25/11=250/11 + 100t + 110t2.

Отсюда получим уравнение движения точки: x = (25 + 100t + 110t2)1/2 (см).

1.1.2. Элементы теории колебаний

Виды колебательных движений материальной точки. Свободные колебания материальной точки

Колебательное движение материальной точки происходит при условии, если на точку

М, отклоненную от положения покоя О, действует сила P , стремящаяся вернуть точку в это положение. Такая сила называется восстанавливающей.

Различают четыре основных случая колебательного движения материальной точки:

свободные колебания, совершающиеся под действием только восстанавливающей силы;

затухающие колебания, совершающиеся под действием восстанавливающей силы и силы сопротивления движению;

вынужденные колебания, совершающиеся под действием восстанавливающей силы

исилы периодического характера, называемой возмущающей силой;

вынужденные колебания, совершающиеся под действием восстанавливающей силы, возмущающей силы и силы сопротивления движению.

Изучим свободные колебания материальной точки. Примем прямолинейную траекторию движения точки М за ось х и поместим начало координат О в положение, в котором точка М могла бы находиться в покое. Если точка М выведена из состояния покоя,

то на нее по оси х действует только восстанавливающая сила P . Если в некоторый момент времени t точка М имеет координату х, то модуль восстанавливающей силы

Р = с · ОМ = с|х|,

где с – коэффициент жесткости пружины, численно равный силе упругости ее при деформации, равной единице.

Составим дифференциальное уравнение прямолинейного движения точки М под

действием восстанавливающей силы P :

m x = ΣXi=Px.

31

Решая и преобразовывая его, получим: (c/m=k2)
x= Asin(kt+β).	(1.11)

Уравнение (1.11) является уравнением гармонического колебательного движения точки. Таким образом, установлено, что свободные колебания материальной точки под

действием линейной восстанавливающей силы являются гармоническими колебаниями.

Амплитуда A и начальная фаза β свободных колебаний материальной точки как постоянные интегрирования определяются по начальным условиям движения: (x0, x 0, t0 = 0);

A=(x02+( x 0/k)2)1/2, tg (β)=kx0/ x 0.

Так как каждому значению тангенса соответствуют два угла в пределах от 0 до 2π, то необходимо определить еще sin(β)=x0/A.

Циклическая частота и период свободных колебаний определятся по формулам: k = (c/m)1/2,

T = 2π/k = 2π(m/c)1/2.

как видно, частота и период свободных колебаний точки зависят лишь от массы этой точки и от коэффициента с, характеризующего восстанавливающую силу, и не зависят от начальных условий движения.

Период свободных колебаний Т увеличивается при увеличении массы точки и уменьшается при увеличении коэффициента с.

График свободных колебаний показан на рис. 1.6.

Рис. 1.6

Свободные колебания груза, подвешенного к пружине

Рассмотрим груз весом G, подвешенный к пружине АВ, конец А которой закреплен неподвижно. Когда груз находится в покое, удлинение пружины равно fст. Положим, что в некоторый момент времени груз был смещен из положения покоя вниз по вертикали на величину у0 и отпущен с начальной скоростью y0 .

Определим возникшее движение груза, пренебрегая массой пружины.

Начальные условия будут: t0 = 0, у = у0, y y0 . На груз действуют силы: сила тяжести

G и сила упругости пружины P , модуль которой пропорционален деформации пружины. Дифференциальное уравнение движения груза имеет вид

m y = ΣYi = G – c(fст + y).

Учитывая, что в положении статического
равновесия G=c fст, получим
y +сy=0.	(1.12)

Уравнение (1.12) является дифференциальным уравнением свободных колебаний материальной точки.

Круговая частота свободных колебаний груза

f			k	,
			2
	32

где k=(c/m)1/2 [c-1].

Период его колебаний

T=1/f=2π/k=2π(m/c)1/2

Представим уравнение движения груза в форме (1.11): y= Asin(kt+β).

Амплитуду A и начальную фазу β колебаний определим, пользуясь начальными условиями:

A=(y02+( y	/k)2)1/2,	tg (β)=ky0/ y	.
0		0
Уравнение движения груза (1.11) примет вид
y Asin((ñ / m)1 / 2 t ) .			(1.13)

Формула (1.13) является общей для определения периода свободных колебаний груза, поддерживаемого упругой связью. Она позволяет определить период свободных колебаний этого груза около положения, в котором действующие на груз силы уравновешиваются.

Эквивалентная жесткость

При последовательном соединении жесткость эквивалентной пружины можно определить по формуле

C C1C2 . C1 C2

При параллельном соединении пружин коэффициент упругости эквивалентной пружины равен сумме коэффициентов упругости данных пружин:

C C1 C2 .

Примеры на свободные колебания

Пример 1. Тело весом G = 20 H, лежащее на гладкой горизонтальной плоскости и прикрепленное к концу недеформированной пружины, отклоняют из положения покоя вправо, растягивая пружину на 4 см, и отпускают, сообщая начальную скорость 56 см/с, направленную влево (удлинение пружины на 1 см вызывается силой 4 H). Определить дальнейшее движение тела, пренебрегая массой пружины.

Решение. Направим ось х горизонтально вправо, считая началом координат О положение покоя тела, принятого за материальную точку. Тогда начальные условия будут следующими:t = 0, хо = 4 см, x о = –56 см/с.

В произвольный момент времени t на тело М, имеющее координату х, действуют силы:

сила тяжести G , реакция плоскости N и сила упругости деформированной пружины P , направленная к точке О.

Составим дифференциальное уравнение движения тела m x = ΣХi= Px= –cx.

Решая и преобразовывая его, получим:

x= Asin(kt+β).

Вычислим частоту и период колебаний: k=(c/m)1/2 =(cg/G)1/2 =14 рад/с; T = 2π/k = 0,45 c.

Амплитуду А и начальную фазу β свободных колебаний тела вычислим по начальным условиям:

33

A=(x02+( x 0/k)2)1/2 =(16+16)1/2≈5,7 см;	β = 135o= 3/4π.
tg(β)=k x 0/x0=14·4/–56= –1; sin(β)=x0/A=√2/2;
Уравнение свободных колебаний груза имеет вид:

х = 5,7 sin (14t +3/4π).

Примечание. Амплитуда свободных колебаний зависит как от начального отклонения тела из положения покоя, так и от начальной скорости. При этом направление начальной скорости не влияет на амплитуду. Так, если начальную скорость направить вправо ( x 0 = 56 см/с), амплитуда будет иметь ту же величину. Если тело опустить без начальной скорости ( x 0 = 0), то амплитуда А=|xo| = 4 см; т. е. амплитуда будет равна начальному отклонению тела от положения покоя.

Наличие начальной скорости увеличивает амплитуду.

Пример 2. Груз весом G подвешен на двух пружинах с различными коэффициентами жесткости с1 и с2. Определить периоды свободных колебаний груза при последовательном и параллельном соединении пружин при условии, что удлинения параллельно соединенных пружин одинаковы (рис. 1.7 и рис. 1.8).

Решение.

а) В случае последовательного соединения пружин (рис. 1.7) общее статическое удлинение связи, поддерживающей груз, равно сумме удлинений двух пружин.

Таким образом, при последовательном соединении пружин приведенный коэффициент жесткости:

Спр с1с1с2с2 .

Период колебаний груза

Т 2	G(с1 с2 ) .
	gс с	2
	1

б) В случае параллельного соединения пружин (рис. 1.8) силы S1 и S2 , растягивающие

пружины, определяются как параллельные составляющие силы G :

S1+ S2=G; S1/S2=l1/l2.

Величина удлинения каждой пружины:

fст=S1/c1=S2/c2=G/(c1+c2).

Период колебаний груза:

Т 2	G			.
	g с с	2
	1

34

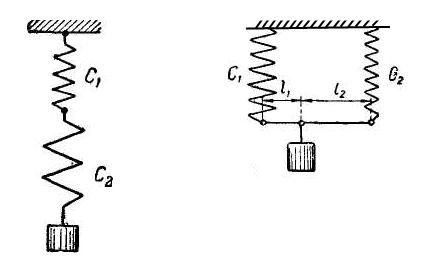
Рис. 1.7 Рис. 1.8

Затухающие колебания материальной точки

Материальная точка, совершающая колебания в реальных условиях, испытывает сопротивление движению (трение, сопротивление воздуха и т. п.). Это означает, что, кроме восстанавливающей силы, направленной к центру колебаний, на точку действует сила сопротивления, направленная всегда в сторону, противоположную направлению движения точки. Закон изменения модуля силы сопротивления зависит от физической природы этой силы. Так, например, модуль силы трения скольжения можно принять постоянным.

Сопротивление воздуха при малых скоростях движения тел считают пропорциональным первой степени скорости, а при больших скоростях, в довольно широких пределах, его принимают пропорциональным квадрату скорости движущегося тела.

Рассмотрим колебания материальной точки М под действием линейной

восстанавливающей силы P и силы сопротивления движению R , пропорциональной скорости точки.

Составим дифференциальное уравнение движения материальной точки под действием сил P и R :

m x = ΣХi= Px+Rx= –cx – αx ;
или, вводя обозначения α/m=2n; и c/m=k2:
x +2n x +k2x = 0.	(1.14)

Уравнение (1.14) является дифференциальным уравнением движения материальной точки под действием восстанавливающей силы и силы сопротивления, пропорциональной скорости движения точки.

Решая дифференциальное уравнение (1.14), получим уравнение движения точки в виде:

x= Ae-ntsin(t·(k2–n2)1/2+β).

(1.15)

Движение, определяемое уравнением (1.15), имеет колебательный характер, так как координата х периодически изменяет свой знак при изменении знака, входящего в уравнение синуса. Множитель e-nt указывает на то, что амплитуда колебаний с течением времени уменьшается.

Колебания этого вида называются затухающими. График затухающих колебаний изображен на рис. 1.9.

35

Рис. 1.9

Пусть в начальный момент t = 0 точка имела координату х0 и проекцию скорости на ось х, равную x 0.

A и β находим по формулам:
А	x2		(x	nx	)2	,
			0	0
	0		k 2 n2

tg(β)=x0(k2–n2)1/2/( x0 +nx0), sin(β)=x0/A.

Частота затухающих колебаний:

k =(k2–n2)1/2 .

Период затухающих колебаний Т* представляет собой промежуток времени между двумя последовательными прохождениями точки в одном направлении через положение покоя (рис. 1.9):

T*=2π/ k =2π/(k2–n2)1/2,

(1.16)

где T = 2π/k период свободных колебаний этой же точки.

Формула (1.16) показывает, что период затухающих колебаний больше периода свободных колебаний точки. Однако при небольшом сопротивлении это увеличение незначительно. В случае небольшого сопротивления период затухающих колебаний можно принимать равным периоду свободных колебаний.

Амплитудой затухающих колебаний называют наибольшие отклонения точки в ту и другую сторону от положения покоя в течение каждого колебания.

Из последовательных значений переменной

	амплитуды можно составить ряд (рис. 3.10): А1, А2, …, Аi,
	Ai + 1, …An.
	Определим отношение последовательных членов ряда
	Ai+1 и Ai, соответствующих моментам времени ti+ 1 = ti +T*/2 и
	ti.
	Ai+1/Ai =e–nT*/2.
Рис. 1.10
	36

Отвлеченное число e–nT*/2 называется декрементом затухающих колебаний; натуральный логарифм декремента, т. е. величина –nT*/2 называется логарифмическим декрементом:

–nT*/2 = –πn/(k2–n2)1/2.

Коэффициент п называют коэффициентом затухания. Затухание колебаний происходит очень быстро, даже при малом сопротивлении.

Таким образом, основное влияние сопротивления на свободные колебания материальной точки выражается в уменьшении амплитуды колебаний с течением времени, т. е. в затухании колебаний.

Апериодическое движение точки

Движение материальной точки теряет колебательный характер и становится апериодическим в случае большого сопротивления, т. е. при n≥k или α≥2*(т/с)1/2 .

а) При n>k корни характеристического уравнения вещественны, отрицательны и различны. Тогда уравнение примет вид

x=Ae-nt sh ((п2 – k2)1/2 t + β).

(1.17)

Уравнение движения точки (1.17) показывает, что рассматриваемое движение точки не является колебательным, так как гиперболический синус не является периодической функцией.

б) При n = k корни характеристического уравнения вещественны, равны и отрицательны. Тогда уравнение примет вид

x= e-nt [x0+( x	+nx0)t].	(1.18)
0

Движение точки, определяемое уравнением (1.18), является также апериодическим.

Вынужденные колебания материальной точки

Вынужденные колебания совершает материальная точка, на которую наряду с восстанавливающей силой действует периодически изменяющаяся сила, называемая

возмущающей силой.

Практически наиболее важным является случай, когда возмущающая сила Q

изменяется по гармоническому закону, т. е. проекция ее на ось х, направленную по траектории точки, определяется

Qx = Hsin(pt+δ),

где Н – максимальный модуль, или амплитуда возмущающей силы;

p – частота изменения возмущающей силы, равная числу полных циклов изменения возмущающей силы за 2π с ;

pt+δ – фаза изменения возмущающей силы;

δ – начальная фаза изменения возмущающей силы.

Период изменения возмущающей силы τ определяется по ее частоте:

τ = 2π/p.

x + k2х = h sin(pt+δ).

Уравнение (1.19) представляет собой дифференциальное уравнение вынужденных колебаний материальной точки (здесь c/m = k2; H/m = h).

Находим искомое частное решение уравнения:

37

	x	h	sin( pt ).	(1.19)
		k2 p2

Общее решение уравнения примет вид

	x Asin(kt β)	h	sin( pt ).	(1.20)
		k2 p2

Уравнение (1.20) показывает, что точка совершает сложное колебательное движение, складывающееся из двух гармонических колебаний.

Первый член правой части уравнения (1.20) определяет свободные колебания, а второй – вынужденные колебания точки.

Таким образом, установлено, что при одновременном действии восстанавливающей и возмущающей сил материальная точка совершает сложное колебательное движение, представляющее собой результат наложения свободных и вынужденных колебаний точки.

Постоянные интегрирования A и β в уравнении (1.20) определяются по начальным условиям движения.

Последний член правой части уравнения (1.20), определяющий вынужденные колебания точки, не содержит постоянных интегрирования, следовательно, вынужденные колебания не зависят от начальных условий движения точки.

Исследуем вынужденные колебания точки. Эти колебания определяются уравнением

	x	h	sin( pt ).
		k2 p2

Частота р и период τ = 2π/p вынужденных колебаний совпадают с частотой и периодом изменения возмущающей силы.

Вынужденные колебания, частота р которых меньше частоты k свободных колебаний точки, называют вынужденными колебаниями малой частоты.

Вынужденные колебания, частота р которых больше частоты k свободных колебаний,

называют вынужденными колебаниями большой частоты.

Фаза вынужденных колебаний

Уравнение вынужденных колебаний малой частоты (при р < k) имеет вид

x		h			sin( pt ).
	k2 p2
В этом случае фаза колебаний pt+δ		совпадает с фазой возмущающей силы и амплитуда
вынужденных колебаний определяется формулой:
		А			h	.
			k	2 p2

В случае вынужденных колебаний большой частоты (при р > k) уравнению придают такой вид, чтобы коэффициент при синусе был положительным:

	x	h	sin( pt ).
		k2 p2

В этом случае амплитуда вынужденных колебаний

	А	h	.
		k2 p2
		38

Амплитуда вынужденных колебаний

Исследуем зависимость амплитуды вынужденных колебаний А от частоты р возмущающей силы. Для этого введем статическое отклонение Ао точки М от начала координат О под действием постоянной силы Н

А0 Hc kh2 .

Отношение ŋ амплитуды вынужденных колебаний АВ к величине Ао называется

коэффициентом динамичности:

при р < k:

А

k2

1

;

В

А0

k2 p2

2

1

p

2

k

при р > k имеем:

А

k2

1

.

В

p2 k2

2

А0

p

1

2

k

Результирующее движение точки определяется уравнением:

			h		p				h
x x cos(kt) x		sin(kt)		sin cos(kt) ...		cos sin(kt)				sin( pt ).	(1.21)
			k 2 p2		k			k 2	p2
0	0

Согласно уравнению (1.21), движение точки М можно рассматривать как результат сложения трех ее движений:

1)свободных колебаний точки, которые возникли бы при отсутствии возмущающей

силы, отклонении точки из положения покоя на расстояние х0 и сообщении ей начальной скорости v0, проекция которой на ось х равна х0:

2)x(1 ) x0cos(kt) x0sin(kt);

3)колебаний, имеющих тоже частоту k, но вызванных действием на точку возмущающей силы:

	x( 2 )			h	sin cos (kt )	h	cos sin (kt );
			k 2	p 2		k

4) вынужденных колебаний точки, частота которых равна частоте возмущающей силы р:

x		h	sin( pt ).
( 3 )		k 2 p2

Явление биений

При частоте возмущающей силы, близкой к частоте свободных колебаний точки, наступает явление, называемое биениями. Полагая в уравнении (1.22) хо = 0 и x о’ = 0, рассмотрим колебания материальной точки, вызываемые лишь действием возмущающей силы:

		x= x (2) + x(3) ;
	и имея в виду, что p/k≈1 и (p+k)/2≈p, получаем:
		2h		t
	x		sin ( p k)		cos( pt ).	(1.22)
		k 2 p2		2
			39

Уравнение (1.22) определяет движение точки, являющееся результатом наложения дополнительных колебаний, вызванных действием возмущающей силы, на собственно вынужденные колебания в случае p≈k.

Обозначим:

	A(t)		2h		( p k)	t
				sin			.
		k2 p2				2
	Тогда уравнение (1.22) примет вид
	x=A(t)·cos (pt+δ).						(1.23)

Движение, определяемое уравнением (1.23), можно рассматривать как колебания частоты p и периода τ = 2π/p, амплитуда которых A(t) является периодической функцией. Период изменения амплитуды:

TА= 4π(p – k).

Так как p≈k, то период TА велик по сравнению с периодом τ = 2π/p.

Явление резонанса

Явление резонанса возникает при совпадении частот вынужденных и свободных колебаний точки: p = k.

В этом случае амплитуда вынужденных колебаний точки равна бесконечности и многие выражения теряют смысл. Дифференциальное уравнение вынужденных колебаний (1.19) при p = k принимает вид

x + k2x = h·sin(kt + δ).	(1.24)
Общее решение дифференциального уравнения (3.24):
x=C1cos(kt)+ C2sin(kt)+ h/(2k)·tsin(kt + δ – π/2).	(1.25)

Уравнение (1.25) показывает, что движение точки М при резонансе является результатом наложения свободных и вынужденных колебаний точки так же, как и при р ≠ k.

Свободные колебания определяются уравнением:

х* = C1cos(kt)+ C2sin(kt).

Вынужденные колебания при резонансе определяются уравнением:

x	**		ht
				sin kt		.	(1.26)
			2k		2

	Частота и период вынужденных колебаний при резонансе
Рис. 1.11, а	равны частоте k и периоду T = 2π/k свободных колебаний точки.

Фаза вынужденных колебаний kt+δ–π/2 отстает от фаз возмущающей силы kt+δ на величину π/2.

Амплитуда вынужденных колебаний при резонансе возрастает пропорционально времени (рис 1.11, б).

40