Manzhosov2

Раздел 3. ТЕОРИЯ УДАРА

Тема 3.1. Явление удара

Цель: знакомство с основными понятиями и определениями, характеризующими явление удара.

Учебные вопросы:

Явление удара, теорема об изменении количества движения механической системы при ударе, теорема об изменении кинетического момента механической системы при ударе.

Изучив данную тему, студент должен:

иметь представление о природе удара, ударной силы и ударного импульса;

знать:

определение удара, ударной силы;

формулу для определения ударного импульса;

формулировку теоремы об изменении количества движения механической системы при ударе;

формулировку теоремы об изменении кинетического момента механической системы при ударе;

законы сохранения кинетического момента механической системы;

уметь:

определять количество движения механической системы;

определять внешний ударный импульс;

находить проекции количества движения системы на любую ось;

определять кинетические моменты; владеть навыками решения задач по теме.

При освоении темы необходимо:

изучить учебный материал по соответствующей теме учебного пособия

акцентировать внимание на отличии движения твердого тела, происходящего под действием обычных сил, от движения, когда скорости точек тела за ничтожно малый промежуток времени получают конечные изменения;

выполнить задание, назначенное преподавателем, по соответствующей теме;

выполнить тестовые задания, касающиеся данной темы;

ответить на контрольные вопросы.

Тема 3.2. Удар двух тел

Цель: знакомство с основными понятиями и определениями, характеризующими удар двух тел.

Учебные вопросы:

Удар двух тел, центр удара.

Изучив данную тему, студент должен:

иметь представление о природе явлений, происходящих при соударении двух тел и влиянии этого процесса на движение данных тел;

знать:

определение удара двух тел;

акцентироватьвниманиенаотличииабсолютноупругогоиабсолютнонеупругогоудара;

понятия центрального удара;

21

уметь:

отличать прямой удар от косого;

находить центр удара;

владеть навыками решения задач по теме.

При освоении темы необходимо:

изучить учебный материал по соответствующей теме учебного пособия;

акцентировать внимание на отличии коэффициента восстановления соударяющихся тел в зависимости от материалов, из которых они изготовлены;

выполнить задание, назначенное преподавателем, по соответствующей теме;

выполнить тестовые задания, касающиеся данной темы;

ответить на контрольные вопросы.

Требования по выполнению и оформлению расчетно-проектировочных работ и контрольных заданий

1.Студент выполняет необходимое количество заданий в соответствии с учебным

планом.

2.Номера схем и исходных данных задаются преподавателем каждому студенту индивидуально.

3.Работы выполняются на стандартных листах писчей бумаги (формата А4) на одной стороне листа (другая остается чистой для возможных исправлений) или в тетради; на обложке должны быть четко написаны: фамилия, имя и отчество студента (полностью).

4.Задание следует выполнять чернилами (не красными), четким почерком, с полями: слева – 20 мм, справа, сверху и снизу – 10 мм. Рисунки выполняются карандашом или чернилами.

5.Перед выполнением каждого задания необходимо написать тему задания, условие (техническое задание) с числовыми исходными данными, составить расчетную схему в масштабе и указать на ней в числах все величины, необходимые для расчета.

6.Решение должно сопровождаться краткими, без сокращения слов, объяснениями и чертежами, на которых все входящие в расчет величины должны быть показаны в числах.

7.При вычислениях в формулы подставляются значения входящих в них параметров в единицах СИ, а затем приводятся окончательные результаты с указанием единиц измерений найденных величин.

8.Рассчитываемый параметр не следует вычислять с большим числом значащих цифр после запятой, вычисления должны соответствовать необходимой точности.

9.После проверки преподавателем расчетного задания студент должен исправить в нем все отмеченные ошибки и выполнить все сделанные ему указания.

Форма контроля

Текущий контроль успеваемости студентов проводится путем проверки уровня подготовки студента к практическому занятию, проверки самостоятельного решения задач, выполнения тестов по теории и практикуму.

Итоговый контроль студентов осуществляется на экзамене.

22

Рис. 1.1

1. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ

1.1. ДИНАМИКА

Введение в динамику

Предмет динамики

Динамикой называется раздел механики, в котором изучается движение материальных тел в зависимости от действующих на них сил.

Динамика представляет собой наиболее общий раздел механики, имеющий особое значение для решения многих практических задач в различных областях техники.

Основные законы механики (законы Галилея–Ньютона)

В основе динамики лежат законы, впервые сформулированные Ньютоном и названные им аксиомами, или законами движения (Axiomata sive leges motus).

1. Закон инерции.

Материальная точка сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие других тел не изменит это состояние.

2. Закон пропорциональности силы и ускорения.

Ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление.

3. Закон равенства действия и противодействия.

Всякому действию соответствует равное и противоположно направленное противодействие.

4. Закон независимости действия сил.

Несколько одновременно действующих на материальную точку сил сообщают точке такое ускорение, какое сообщила бы ей одна сила, равная их геометрической сумме.

Законы классической механики подтверждаются опытами и наблюдениями, а потому являются объективными законами природы.

Первый закон – закон инерции, установленный Галилеем, характеризует стремление тела сохранить неизменной скорость своего движения, или иначе сохранить приобретенное им ранее механическое движение.

Это свойство тела называется его инертностью. Движение материи, его вечность и несотворимость имеет как бы свою обратную сторону, свое другое проявление – инертность.

Второй закон – закон пропорциональности силы P и ускорения w устанавливает, как изменяется скорость движения материальной точки под действием силы (рис. 1.1).

Этот закон выражается следующим образом (при m = const):

P mw.

Это соотношение, устанавливающее связь между силой P , массой т

и ускорением w , является важнейшим в классической механике и называется основным уравнением динамики.

Такую форму второму закону придал Эйлер в своем трактате «Механика» (1736). У Ньютона этот закон выражался следующим соотношением:

P t t0 m v v0 .

Масса есть мера инертности материальных тел при их поступательном движении.

23

Современной физикой установлено, что масса тела увеличивается с возрастанием скорости его движения, т. е. масса и энергия взаимосвязаны.

В классической же механике масса движущегося тела принимается равной массе покоящегося тела, т. е. рассматривается как постоянная величина.

Векторному равенству соответствует числовое равенство

P = mw.

Из этого равенства масса может быть определена по формуле m wP .

Системы единиц механических величин

Для измерения механических величин применяются две системы единиц: физическая и техническая.

В физической системе механических единиц за основные единицы приняты единицы длины, массы и времени, а сила является величиной производной и имеет размерность:

[F] = [L1M1T--2].

В технической системе механических единиц за основные единицы приняты единицы длины, силы и времени, а масса является величиной производной и имеет размерность:

[m] = [L–1F1T2].

ВСССР, а ныне в России в качестве национального стандарта принята Международная система единиц измерения СИ (SI – от ‘Le systeme international d'unites’), в механике МКС,

которая так же, как и система СГС, является физической системой единиц. Система единиц измерения МКГСС является технической системой единиц.

За единицу массы в системе МКС принимается масса, равная одному килограмму (кг)

платинового эталона, хранящегося в архиве Французской республики, а за единицу силы – ньютон (Н) – сила, сообщающая массе 1 кг ускорение 1 м/с2.

1 ньютон (Н) = 10 дециньютон (дН) = 100 сантиньютон (сН) = 1000 миллиньютон (мН). 1 килоньютон = 10 гектоньютон (гН) = 100 деканьютон (дан) = 1000 ньютон.

Всистеме СГС за единицу массы принимается грамм (г), а за единицу силы – дина – сила, сообщающая массе 1 г ускорение 1 см/с2.

Всистеме МКГСС за единицу силы принимается килограмм-сила (кгс), сообщающая массе 1 кг ускорение 9,80665 м/с2.

За единицу массы в этой системе принимается техническая единица массы (т. е. м.), т. е. масса, которой сила 1 кгс сообщает ускорение 1 м/с2.

1 ньютон = 105 дин = 0,102 кгс. 1 кгс = 9,81 ньютон = 981 000 дин. 1 т. е.м. = 9,81 кг.

Из второго закона следует, что если сила, действующая на точку, равна нулю, то и ускорение точки равно нулю, т. е. точка, не взаимодействующая с другими телами, или движется равномерно прямолинейно, или находится в покое.

Таким образом, первый закон динамики можно рассматривать как следствие более общего второго закона.

Система отсчета, в которой проявляются первый и второй законы, называется инерциальной системой отсчета. Для большинства задач за такую систему отсчета можно принять систему осей, связанных с Землей.

24

В случае, если необходимо учитывать суточное вращение Земли, за инерциальную систему отсчета принимают геоцентрическую систему осей координат с началом в центре Земли и осями, направленными к трем выбранным «неподвижным» звездам.

При решении астрономических задач пользуются гелиоцентрической системой осей координат с началом в центре Солнца и осями, направленными к трем выбранным «неподвижным» звездам. Эту систему с большей степенью точности можно принять за инерциальную систему.

Третий закон – закон равенства действия и противодействия двух тел отражает двусторонность механических процессов природы. Этот закон устанавливает, что при взаимодействии двух тел, в каком бы кинематическом состоянии они ни находились, силы, приложенные к каждому из них, равны по модулю и направлены по одной прямой в противоположные стороны. Будучи приложенными к разным телам, эти силы не уравновешиваются.

Таким образом, сила инерции материальной точки является реальной силой, представляющей собой противодействие материальной точки изменению ее скорости, и приложена к телу, сообщающему этой точке ускорение.

Сила инерции является одним из важнейших понятий динамики.

Действие сил инерции учитывается при решении многих технических задач и, в частности, при определении реакций связей движущейся несвободной механической системы.

Четвертый закон – закон независимости действия сил – не был сформулирован Ньютоном как отдельный закон механики, но он содержится в сделанном им обобщении правила параллелограмма сил.

Положим, что на материальную точку М действуют

силы: P1 , P2 ,..., Pn (рис. 1.2).

Согласно четвертому закону, ускорение материальной точки, находящейся под действием этих сил, определяется уравнением

mw P1 P2 ... Pn

Таким образом, закон независимости действия сил равносилен утверждению, что ускорение w , получаемое материальной точкой от одновременно действующей на нее системы сил, равно геометрической сумме ускорений, сообщаемых этой точке каждой из сил в отдельности.

Четвертый закон, так же как и остальные законы классической механики, подтверждается опытами и наблюдениями.

1.1.1. Динамика свободной материальной точки

Дифференциальные уравнения движения свободной материальной точки в декартовых координатах

Рассмотрим движение материальной точки М массой т под действием приложенных к ней сил P1 , P2 ,..., Pn . Выберем прямоугольную систему осей координат х, у, z.

Основное уравнение динамики имеет вид

	P2	... Pn .	(1.1)
mw P1

25

Из кинематики известно, что проекция ускорения точки на каждую ось декартовых координат равна второй производной по времени от соответствующей координаты точки, т. е., проектируя обе части векторного равенства (1.1) на координатные оси, получаем:

..			... X n X i
m x X1 X 2
..		Y2 ... Yn Yi
m y	Y1			,	(1.2)
..			... Z n Zi
m z Z1		Z2

где X1, Y1 , Z1; ...; Xn, Yn, Zn – проекции сил P1 , P2 ,..., Pn на оси x, y, z.

Уравнения (1.2) называются дифференциальными уравнениями движения материальной точки.

Естественные уравнения движения материальной точки

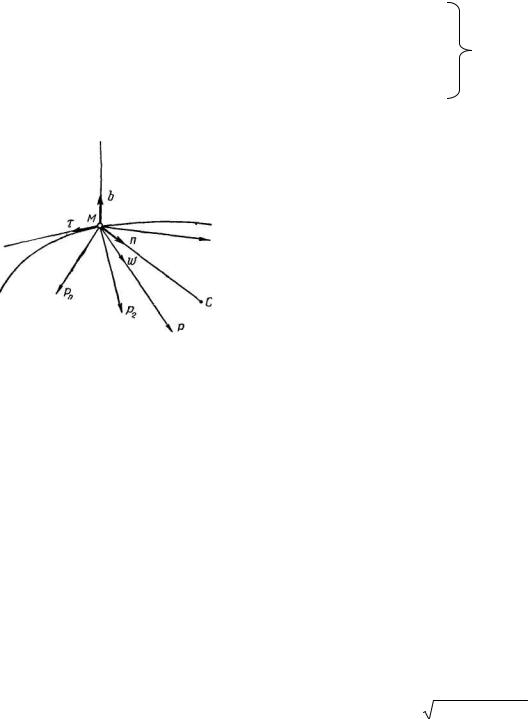
Спроектируем обе части векторного равенства (1.1) на естественные координатные оси (подвижные) – касательную, главную нормаль и бинормаль (рис. 1.3):

Проекции ускорения на касательную и главную нормаль определяются по формулам из кинематики, т. е.

Рис. 1.3		md 2 s
				Pi cos Pi ,		;
		dt	2
mv 2	Pi cos Pi , n .					(1.3)
p

Из кинематики известно, что вектор ускорения w лежит в соприкасающейся плоскости, и сумма проекций всех сил, приложенных к точке, на бинормаль равна нулю:

Pi cos( Pi , b ) 0 .

Уравнения (1.3) называются естественными уравнениями движения материальной точки. Этими уравнениями удобно пользоваться в случае, когда известна траектория точки.

Две основные задачи динамики точки

При помощи дифференциальных уравнений движения точки можно решать две основные задачи динамики точки.

Первая задача динамики. Зная массу точки т и уравнения ее движения: x = f1(t), y = f2(t), z = f3(t), найти модуль и направление равнодействующей сил, приложенных к точке.

Эта задача легко решается следующим путем:

	X mx ,	Y my ,		Z mz ,			P	X 2 Y 2 Z 2 ,
		X			Y				Z
	cos(P,i )		,	cos(P, j)		,	cos(P, k )			.
		P			P				P
				26

Вторая задача динамики. Зная силы, действующие на материальную точку, ее массу т, а также начальное положение точки и ее начальную скорость, получить уравнения движения точки.

Для решения этой задачи необходимо в левую часть уравнений (1.2) подставить значение массы т, а в правую часть – суммы проекций приложенных сил и полученные уравнения дважды проинтегрировать по времени. Эта задача имеет большое практическое значение и в общем случае является более сложной, чем первая.

При интегрировании каждого дифференциального уравнения движения точки появляются две постоянные, а потому при интегрировании трех дифференциальных уравнений движения точки будет шесть постоянных. Значения этих постоянных определяют по начальным условиям движения: значениям трех координат точки и проекций ее скорости на три оси в некоторый момент времени, обычно (но не обязательно) в начальный момент.

Свободное падение тела без учета сопротивления воздуха

Рассмотрим движение тела М, падающего на поверхность Земли с высоты Н, полагая вес тела G постоянным.

Пренебрегая размерами тела, будем считать его материальной точкой. Сначала рассмотрим падение тела в пустоте, т. е. без учета сопротивления воздуха.

Направим ось у по траектории прямолинейного движения тела в сторону его движения и примем за начало координат начальное положение тела. Если начальная скорость тела равна нулю, то начальные условия рассматриваемого движения будут иметь вид

t = 0, y0 = 0, y0 0 .

Уравнения, характеризующие свободное падение тела, примут вид

y	gt ,
y	gt	2	.	(1.4)
	2

Законы свободного падения тела, выраженные этими уравнениями, были впервые экспериментально установлены Галилеем:

1.Скорость свободно падающего тела пропорциональна времени падения (1.7).

2.Пути, проходимые свободно падающим телом, пропорциональны квадрату времени падения.

Пользуясь уравнением (1.4), можно определить время свободного падения тела с высоты Н:

H	gt2	tH	2H	.
	H ,		g
	2

Движение тела, брошенного под углом к горизонту, без учета сопротивления воздуха

Определим движение тела М, брошенного под углом к горизонту с начальной скоростью v0 , пренебрегая сопротивлением воздуха и принимая тело за материальную точку

(рис. 1.4).

27

Рис. 1.4

Совместим начало координат О с точкой вылета тела, направив ось х по горизонтали вправо, а ось у – вверх по вертикали.

Тогда получим начальные условия движения

t = 0, x0 = 0, y0 = 0, x0	v0x v0 cos ,	y0	v0 y v0 sin ;
	x v0 cos ,		(1.5)
	x v0t cos .		(1.6)

Уравнения (1.5) и (1.6) показывают, что проекция скорости тела на горизонтальную ось постоянна и горизонтальное перемещение тела совершается по закону равномерного движения со скоростью v0 cos α, т. е. по инерции.

y v0 sin gt ,				(1.7)
y v t sin	gt	2	.	(1.8)
0	2

Уравнения (1.7) и (1.8) показывают, что вертикальное движение тела является равнопеременным. При подъеме оно замедленное, так как направления вертикальной составляющей скорости и ускорения силы тяжести противоположны, а при спуске – ускоренное, так как эти направления совпадают.

Исключим время t из уравнений движения тела (1.6) и (1.8), получим уравнение траектории:

y xtg	gx2
		.
	2v02 cos2

Траектория представляет собой параболу с вертикальной осью и вершиной в наивысшей точке. Форма траектории тела, движущего в пустоте под действием силы тяжести, была впервые установлена Галилеем.

Определим скорость движения тела по траектории способом проекций:

v vx2 vy2 v0 cos 2 v0 sin gt 2 .

Эта формула показывает, что движение, полученное сложением равномерного горизонтального и равнопеременного вертикального движений, не является равнопеременным.

Определим дальность и продолжительность полета тела. В точке М4 падения тела на землю y4 = 0.

Продолжительность полета определим из уравнения (1.8) при y = 0,

Отсюда получим момент вылета t = 0 и момент падения t4 2v0 sin . g

Дальность полета определим, подставив значение t4 в уравнение (1.6): 28

L x4	v	cos 2v		sin		v2		.	(1.9)
	0		0			0
		g				g sin 2

Формула (1.9) показывает, что дальность полета тела при одной и той же скорости вылета тела v0 зависит от угла α. Очевидно, что наибольшая дальность полета наблюдается при sin2 α =1, т. е. при α = 45°.

Наибольшую высоту подъема тела при заданной начальной скорости v0 и угле α можно определить из условия, что в наивысшей точке М2 проекция скорости на вертикальную ось равна нулю:

v2 y y2 v0	sin gt2			0,
H y2		v2 sin2			.	(1.10)
		0
		2g

Движение материальной точки под действием силы тяжести является примером движения под действием силы, постоянной по модулю и направлению.

Движение падающего тела с учетом сопротивления воздуха

Рассмотрим влияние сопротивления воздуха на движение тела, падающего на землю. Положим, что тело М весом G движется вниз без начальной скорости из точки О,

принятой за начало координат. Ось у направим вертикально вниз. Тогда начальные условия движения будут иметь вид

t = 0; y0 = 0; y0 0.

Рассмотрим падение тела при сопротивлении воздуха, пропорциональном скорости движения тела. Тогда силу сопротивления можно представить в виде R = av, где α – коэффициент пропорциональности.

Обозначим αm k .

Коэффициент k равен модулю силы сопротивления воздуха, приходящейся на единицу массы движущегося тела при скорости его, равной единице, и имеет размерность (с–1).

Составим дифференциальное уравнение движения тела под действием силы тяжести G и силы сопротивления воздуха R:

тy G R mg mkv ,

решая которое получим уравнение движения падающего тела с учетом сопротивления воздуха:

	gt		g(1 e kt )		Рис. 1.5
	y k			.
			k 2

Пример интегрирования дифференциальных уравнений движения точки для случая силы, зависящей от времени

Пример. На точку М массой m = 2 г действует горизонтальная сила P , остающаяся параллельной некоторой прямой и имеющая величину Р = 2cos(5t) мН. Определить движение точки М в горизонтальной плоскости, если в начальный момент скорость точки v0

была перпендикулярна к направлению силы P и имела модуль vo= 10 см/с.

29

Решение. Примем начальное положение точки за начало координат (рис. 1.5). Направим ось х вдоль начальной скорости точки v0, а ось у – параллельно линии действия

силы P .

Тогда начальные условия движения будут следующими:

t =0; х0 = 0; у0 = 0; x0 = vQ = 10 см/с; y0 = 0.

Единственной силой, действующей на точку в горизонтальной плоскости, является

заданная сила P , параллельная оси у.

Составим два дифференциальных уравнения движения точки:

тx Хi 0; тy Yi P.

Из первого дифференциального уравнения x = 0.

Проинтегрировав это уравнение дважды по t, получим:

x = C1; x=C1t+C2.

Подставив в первое уравнение проекцию начальной скорости x = 10 см/с, получим

С1= 10.

Подставив во второе уравнение t = 0, хо = 0, получим С2 = 0. При этих значениях С1 и С2 для движения точки вдоль оси х: x = 10 см/с; х=10t (см).

Получим второе дифференциальное уравнение, выражая массу точки в граммах, а силу Р в динах:

y = 100cos(5t).

Проинтегрировав его дважды по t, получим: y = 20sin(5t); y = –4cos(5t) + C3t + C4.

Подставив в первое уравнение t = 0, уо = 0, найдем С3 = 0.

Подставив во второе уравнение t = 0, уо= 0, получим: 0 = –4 + С4, откуда С4 = 4. При найденных значениях С3 и С4 для движения точки вдоль оси у

y = 20sin(5t) (см/с),

у = 4(1 – cos5t) (см).

Чтобы получить уравнение траектории точки, исключим время из уравнений ее движения:

t = x/10; y = 4(1 – cos(x/2)).

Пример интегрирования дифференциального уравнения движения точки для случая силы, зависящей от положения точки

Пример. Материальная точка М массой т = 20 г отталкивается от некоторого центра О c силой, обратно пропорциональной кубу расстояния ОМ. В начальный момент известны: расстояние ОМ = 5 см, скорость точки v0 = 10 см/с, направленная по прямой ОМ от центра О, и сила отталкивания P = 0,4 мH.

Получить уравнение движения точки под действием силы отталкивания, а также определить скорость, приобретенную точкой на расстоянии 20 см от центра О.

Решение. Центр отталкивания О примем за начало координат, ось х направим по прямой, соединяющей этот центр с движущейся точкой М.

Установим начальные условия:

t = 0, x0=OM0=5 см; x 0 = v0 = 10 см/с.

На точку действует сила отталкивания P , направленная по оси х. Модуль этой силы обратно пропорционален кубу расстояния ОМ, т. е. P = k/x3.

30