МАТЕМАТИЧЕСКИЙ ПРАКТИКУМ

г) угол между стороной АВ и медианой АМ; д) координаты точки пересечения медианы АМ и высоты ВН; е) расстояние от вершины С до стороны АВ.

Решение.

а) Известны координаты двух точек. Поэтому воспользуемся уравнением (4).

x − 2	=	y + 2	;	x − 2	=	y + 2	-каноническое уравнение прямой АВ. При-
3 − 2 1+ 2				1	3

ведем это уравнение к общему виду. 3(x − 2) = y + 2; 3x − y − 8 = 0

- искомое

уравнение в общем виде.

б) Медиана АМ делит сторону ВС пополам. Найдем координаты точки

М. Используем

формулы

координат середины отрезка.

x =

x1 + x2

,

2

y =

y1 + y2

, где (x ; y )

и (x ; y

)

координаты концов отрезка. x =

3

− 4

= −0,5;

2

1

1

2

2

2

y = 1+ 2 =1,5. М(-0,5;1,5). Уравнение медианы запишем с помощью уравне- 2

ния прямой (4), проходящей через две данные точки.

	x − 2		=	y + 2	;	x − 2	=	y + 2		. Или, в общем виде, 3,5x + 2,5y − 2 = 0.
	− 0,5 −					− ,5
		2	1,5 + 2				3,5
Умножим обе части уравнения на 2.									Уравнение медианы АМ: 7x + 5y − 4 = 0 .

в) Высота ВН треугольника АВС перпендикулярна к стороне АС. Сле-

→

довательно, вектор АС = {− 6;0} является нормальным для прямой ВН. Ис-

пользуем уравнение (2).

− 6(x − 3) + 0(y −1) = 0. Уравнение высоты ВН: x − 3 = 0. Прямая ВН параллельна оси ОУ.

→

→

г) Нормальные векторы прямых АМ и АВ N1

= {7;5} и N2

= {3;−1} соот-

ветственно. сosα =

N N

r

2

2

r 1

r2

. N1 N 2= 7 3+ 5 (−1) =16,

N1

=

7 + 5

= 74 ,

r

N1

N2

N

2

= 32 + (−1)2

= 10 .

41

сosα =		16				=		8		=		8		; α = arccos		8		.
								37 5
		74 10							185				185

д) Чтобы найти координаты точки пересечения прямых АМ и ВН, решим систему из уравнений этих прямых

7x + 5y − 4		= 0;	x = 3;	.
	= 0
x − 3			y = −3,4

е) расстояние от точки С(-4;-2) до прямой АВ: 3x − y − 8 = 0

находим по

Ax0

+ By0 + C

3 (−4) − (− ) − 8

18

формуле d =

. d =

=

=1,8 10 .

A2 + B2

32 + (−1)2

10

Пример 2. Найти координаты точки В, симметричной точке А(2;-3) относительно прямой l :3x − 5y +13 = 0. Составить уравнение прямой, проходящей через точку В параллельно прямой l .

Решение.

Точка В лежит на прямой m, перпендикулярной прямой l , проходящей через точку А. Составим уравнение этой прямой.

3

Угловой коэффициент прямой l : k = , тогда угловой коэффициент

1 5

перпендикулярной прямой k

= −

1

= −

5

. Воспользуемся уравнением прямой

2

k1

3

(6). y + 3 = −

5

(x −

) ; 3y + 9 = −5x +10 ;

5x + 3y −1= 0. Точка

пересечения

3

прямых l

и m является проекцией точки А на прямую l , а также, серединой

отрезка

АВ.

Ее

координаты

являются решением

системы

уравнений

3x − 5y +13 = 0;

x = −1; y = 2.

5x + 3y −1= 0.

Решение системы

Тогда координаты точки В можно найти, используя формулы коорди-

нат середины отрезка x =

x1 + x2

; y =

y1 + y2

.

2

2

-1=

2 + x2

;

2

= − 3 + y2 ;

x

= −4, y

= 7. Точка

В имеет

координаты

2

2

2

2

(-4;7).

42

Составим уравнение прямой, проходящей через точку В параллельно прямой l . Так как прямые параллельны, их угловые коэффициенты равны. Используем уравнение прямой (6).

y − 7 = 3(x + 4); 5y − 35 = 3x +12; 3x − 5y + 47 = 0 искомое уравнение. 5

Задачи для самостоятельного решения.

1.В треугольнике АВС составить уравнения медианы и высоты, проведенных из вершины А. A(−4;2), B(−7;7), C(−13;−13).

2.В треугольнике АВС составить уравнение прямой, проходящей через вершину А перпендикулярно медиане BM . A(0;4),

B(2;6), C(8;−2) .

3.В треугольнике АВС найти проекцию вершины В на сторону АС. A(2;4) , B(4;10), C(6;−2).

4.Составить уравнения прямых, проходящих через точку

A(2;1):а) параллельно прямой 3x + 2y − 5 = 0; б) перпендикулярно прямой A(2;1)3х+4у-2=0.

5. Зная координаты вершины A(1;3) треугольника АВС и уравнения двух его медиан x − 2y +1= 0; y −1= 0 составить уравнения всех сторон треугольника.

6. Пусть стороны АВ, ВС и АС треугольника АВС лежат на прямых, имеющих следующие уравнения: x + y +1= 0; x − 4y − 9 = 0; x + 6y +1= 0. Составить уравнения высоты, проведенной из вершины А.

7.Пусть стороны АВ, ВС и АС треугольника АВС лежат на прямых, имеющих следующие уравнения: 2x + y − 2 = 0 ; 5x + y − 2 = 0; x =1. Написать уравнение медианы, проведенной из вершины В.

8.Найти точку В* симметричную точке B(3;5) относительно

прямой, проходящей через точки A(0;1) и C(8;−3).

9.Даны координаты вершин четырехугольника АВСD :

A(0;1) , B(3;6), C(8;2), D(5;−2). Найти угол между диагональю АС и стороной АD.

10. Даны вершина A(2;6) треугольника АВС и уравнения высот y = x и y = −2x, проходящих через вершины В и С. Написать уравнение стороны ВС треугольника АВС.

11. Одна из сторон квадрата лежит на прямой 3x + 2y − 7 = 0, а координаты одной из вершин квадрата A(−2;3). Найти площадь этого квадрата.

43

12. Одна из вершин квадрата A(1;2) лежит на стороне, уравнение которой 2x + y − 4 = 0 . Написать уравнение диагонали квадрата, выходящей из точки А.

13.Найти точку А* симметричную точке A(2;4) относительно прямой 2x + 3y −12 = 0. Сделать чертеж.

14.В треугольнике АВС: A(−2;2), B(2;5) , C(6;−4). Написать

уравнение биссектрисы, выходящей из вершины А.

15. Даны координаты трех последовательных вершин параллелограмма АВСD: A(−4;2), B(0;6), C(6;−2). Найти координаты вершины D. Написать уравнение диагонали ВD.

16.Написать уравнение прямой, проходящей через точку

A(2;−3) и точку М, делящую отрезок ВС в отношении 3:2, где B(4;1), C(6;4) .

17. Найти точку пересечения медиан треугольника АВС: A(0;2), B(4;1), C(2;−6) .

3.2 Плоскость и прямая в пространстве.

Плоскость. Общее уравнение плоскости:			,

где A, B, C - координаты нормального вектора.

Если в этом уравнении D = 0, то плоскость проходит через начало коорди-

нат, и ее уравнение примет вид				.

Существуют различные способы задания плоскости и соответствующие им виды ее уравнения.

1. Уравнение плоскости, проходящей через точку перпендикулярно вектору :

																									.
2.	Уравнение плоскости в «отрезках»:
	где a, b, c																											,
				абсцисса, ордината и аппликата точек пересечения плоско-
	стью координатных осей Ох, Оу Оz соответственно.
3.	Уравнение			плоскости,									проходящей													через три данные точки
				,								,														:

44

,

4. Нормальное уравнение плоскости:

,

где

- длина перпендикуляра, опущенного из начала координат на

плоскость; , , 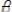– углы, образованные единичным вектором , име-

ющего направление указанного перпендикуляра, с осями Ох, Оу и Оz ().

Рассмотрим простейшие задачи.

I.Пусть даны две плоскости

,

.

Величина угла между плоскостями и вычисляется на основа-

нии формулы

,

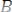
где и - нормальные векторы данных плоско-

стей.

Условие перпендикулярности данных плоскостей:

, или				.

Условие параллельности двух плоскостей:

.

II. Расстояние d от точки						до плоскости

,

вычисляется по формуле

.

Пример 1.Написать уравнение плоскости, параллельной оси Ох и проходящей через точки и .

Используем уравнение плоскости и координаты точки , получим

.

45

Так как плоскость параллельна оси Ох, то . Уравнение плоскости примет вид

.

Подставляя в это уравнение координаты точки

, получим

,

,

.

Искомое уравнение примет вид

.

Поделив обе части уравнения на

(

, так как если

, то и

,

но нормальный вектор

не может быть нулевым вектором), получим

,

,

,

уравнение, которое и является искомым уравнением плоскости.

Пример 2. Написать уравнение плоскости, проходящей через точку параллельно плоскости .

Так как искомая плоскость параллельна данной, то нормальный вектор искомой плоскости совпадает с нормальным вектором данной плоскости, т.е.

. Используя уравнение плоскости

и координаты точки

, получим

,

или

.

Пример 3. Написать уравнение плоскости, проходящей через точку

и параллельной векторам

.

Воспользовавшись

уравнением

плоскости

, получим

.

и

, то в качестве ее нормального

Так как плоскость параллельна векторам

вектора

можно взять вектор

. Используя формулу

,

получим

46

.

Подставляем в уравнение

,

упрощаем и получим искомое уравнение

.

Эту задачу можно решить другим способом.

Возьмем произвольную точку искомой плоскости - . Найдем ко-

ординаты вектора . Векторы , и компланарны, следовательно, их смешанное произведение равно нулю, т.е.

,

раскрывая определитель, получим

.

Прямая в пространстве. В зависимости от способа задания прямой в пространстве рассматриваются различные способы ее задания.

1. Канонические уравнения прямой, проходящей через данную точку

параллельно вектору

,

:

где направляющий вектор этой прямой.

2. Параметрические уравнения прямой:

где переменный параметр, .

3. Уравнения прямой, проходящей через две точки		и

:

.

4.Общие уравнения прямой в пространстве.

Две пересекающиеся плоскости определяют прямую:

где нормальные вектора этих плоскостей не коллинеарные. Направляющий вектор этой прямой находится по формуле

47

.

Рассмотрим случаи взаимного расположения двух прямых в пространстве. Пусть даны две прямые

и

,

а также плоскость

.

Для двух прямых в пространстве возможен один из вариантов взаимного расположения

a)параллельны;

b)совпадают;

c)пересекаются;

d)скрещиваются.

Влюбом случае прямые образуют некоторый угол (между их направляющими векторами и ):

,

где

и

- направляющие векторы данных

прямых.

Отсюда следует условие перпендикулярности прямых:

или

.

Условие параллельности прямых имеет вид:

а условие их совпадения

,

,

где

и

точки, принадлежащие прямым и .

Необходимое и достаточное

условие

пересечения непараллельных прямых

(

), запишется в виде:

или

,

если это условие не выполняется, то прямые скрещивающиеся.

Расстояние h от точки до прямой, проходящей через точку параллельно вектору вычисляется по формуле

48

.

Пример 4. Преобразовать общие уравнения прямой к каноническому виду

Для решения этой задачи необходимо найти направляющий вектор и ка- кую-нибудь точку, принадлежащую этой прямой.

Направляющий вектор находим по формуле

.

Точку на прямой будем искать следующим образом: примем , тогда система примет вид

Решив эту систему, найдем

,

, получим точку

,

лежащую на прямой.

Канонические уравнения прямой запишутся в виде:

.

Пример 5. Написать параметрические уравнения прямой, проходящей через

точку

, параллельно вектору

.

Используя

данные условия задачи, запишем канонические уравнения пря-

мой:

.

Приравняем каждое из отношений к параметру t, получим

-параметрические уравнения прямой.

Пример

6. Найти расстояние от точки

до прямой

.

в направлении векто-

По условию, прямая проходит через точку

ра

. Найдем координаты вектора

и выполним

необходимые вычисления, используя формулу

49

,

,

,

,

.

Прямая и плоскость в пространстве. Пусть даны прямая

,

где направляющий вектор этой прямой, и плоскость

,

где

- нормальный вектор плоскости.

Угол между прямой и плоскостью

определяется по формуле

Условие параллельности прямой (l) и плоскости () имеет вид

Am + Вn + Ср = 0 ;

условие их перпендикулярности:

.

Для нахождения точки пересечения прямой и плоскости удобно воспользоваться параметрическими уравнениями прямой

координаты точки пересечения находятся из системы уравнений

Условие, при котором прямая (l) лежит в плоскости :

50