
- •Введение
- •Некоторые сведения о методиках динамического расчета артиллерийских орудий
- •Глава 1 математическая модель действия выстрела на артиллерийское орудие
- •1.1. Выбор и обоснование расчетной схемы
- •1.2 Анализ конструкций современных образцов артиллерийских орудий
- •Глава 2
- •Движение при наличии связей.
- •Уравнения лагранжа второго рода при нестационарном базисе
- •Основные понятия
- •2.1. Несвободное движение точки.
- •2.2 Связи и их классификация
- •2.3.Возможные и виртуальные перемещения
- •2.4 Обобщенные координаты. Число степеней свободы механической системы
- •В различных случаях
- •2.5. Несвободное движение системы материальных точек
- •2.6. Виртуальная работа силы. Идеальные связи
- •2.7. Обобщенные силы
- •2.8. Уравнения Лагранжа второго рода
- •2.9. Последовательность действий при использовании уравнений Лагранжа второго рода для решения задач о движении голономных систем с несколькими степенями свободы
- •Движении:
- •3.2. Углы Эйлера.
- •3.3.Формулы преобразования координат. Поворотные матрицы
- •3.4. Мгновенная угловая скорость и угловое ускорение Кинематические уравнения Эйлера
- •3.5. Скорость и ускорение точек тела. Формула Ривальса
- •Расчетная работа № 1 – Тема: кинематика вращения твердого тела вокруг неподвижной точки случай регулярной прецессии
- •4.1. Схемы конструкций и таблица к ним с исходными данными к расчетной работе «№1»
- •4.2.Методические указания и план решения расчетной работы № 1
- •4.3. Пример 4.1решения расчетной работы № 1 (рис.4.3). Тема: вращение твердого тела вокруг неподвижной точки
- •4.4. Пример 4.2 решения расчетной работы №1 (рис.4.4). Тема: вращение твердого тела вокруг неподвижной точки
- •5.2. Пример 5.1 выполнения второй расчетной работы №2
- •Курсовая работа тема:
- •Расчет динамических моделей объектов вооружения
- •Конкретных конструктивно компоновочных схем по учебной дисциплине «динамика конструкций»
- •.Методические указания и примеры выполнения
- •Пример 6.2 выполнения расчетной работы по динамике несвободной механической системы с тремя степенями свободы (рис.6.3.1)
- •Окончательный вид уравнений Лагранжа второго рода или дифференциальные уравнения движения рассматриваемой системы в обобщенных координатах
- •Пример 6.3 выполнения расчетной работы по динамике несвободной механической системы с тремя степенями свободы
- •Литература Основная литература
- •Дополнительная литература
- •Глава 3. Вращение твердого тела вокруг неподвижной точки .44
- •Глава 4. Расчетная работа № 1–тема: вращение твердого
2.9. Последовательность действий при использовании уравнений Лагранжа второго рода для решения задач о движении голономных систем с несколькими степенями свободы
1) Определить число степеней свободы системы и выбрать наиболее удобные обобщенные координаты;
2) Вычислить кинетическую энергию системы
в ее абсолютном движении и выразить эту
энергию через обобщенные координаты
![]() и обобщенные скорости
и обобщенные скорости![]() ;
;
Напомним формулы кинетических энергий в абсолютном
Движении:
материальная точка :
![]() ;
;
система материальных точек :
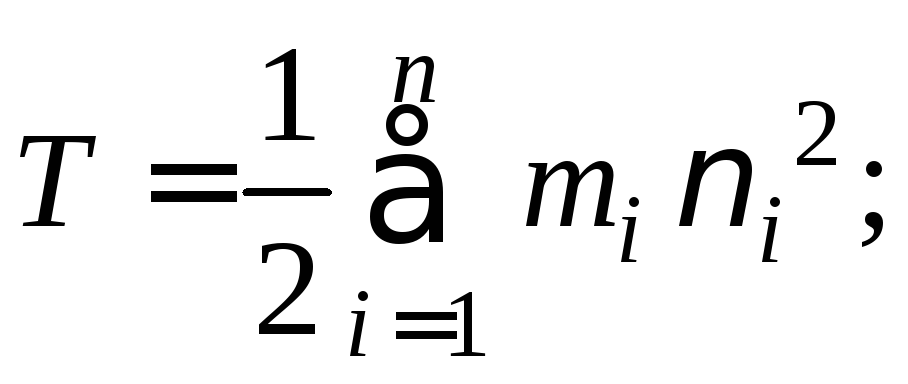
твердое тело:
при поступательном движении:
![]() ;
;
при вращении
вокруг неподвижной осиl:
![]()
при плоско-параллельном движении:
![]()
![]()
при вращении вокруг неподвижной точки:
![]()
в общем случае движения твердого тела :
![]()
![]()
3) Вычислить производные от кинетической энергии, входящие в левую часть уравнений Лагранжа;
4) Определить обобщенные силы, соответствующие выбранным обобщенным координатам (так как каждой обобщенной координате соответствует обобщенная сила, то число обобщенных сил механической системы равно числу обобщенных координат, причем размерность каждой из обобщенных сил соответствует размерности соответствующей обобщенной координаты);
5) Подставить все вычисленные величины в уравнения Лагранжа.
Пример 2.14. Механическая система, показанная на рис.2.13,
состоит из однородного круглого цилиндра 1массойm1и радиусом
r , однородного стержня2длинойl и массойm2, к которому в точкахАиВшарнирно прикреплены ползуны3и 4массамиm3 иm4,
также двух пружин, коэффициенты жесткости которых С1иС2 соответственно. Цилиндр без скольжения катится по горизонтальной плоскости. К нему приложена пара сил с моментомМ1 (t ).

Рис. 2.13
Пренебрегая сопротивлением качению цилиндра 1, трением в шарнирах и направляющих, а также массой пружин, составить дифференциальные уравнения движения системы.
Решение. Система имеет две степени свободы. В качестве обобщенных координат выберем перемещение q1 = sцентра массС цилиндра1и угол q2 = поворота стержня2( против хода часовой стрелки). Полагаем, что приs=0и =0пружины не деформированы.
Уравнения Лагранжа второго рода для данной системы имеют вид
 (2.42)
(2.42)
Кинетическая энергия системы складывается из кинетических энергий
цилиндра 1и стержня2, совершающих плоское движение;
ползунов 3и4, совершающих поступательное движение:
T=![]() +
+![]() +
+![]() +
+ ![]() .
.
Кинетическая энергия цилиндра 1:
![]() Так как
Так как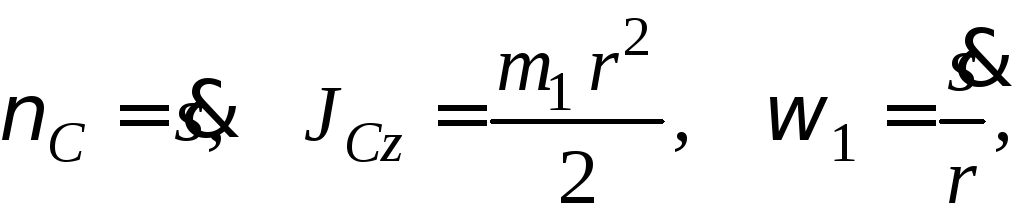 то
то
![]()
Кинетическая энергия стержня 2:
![]() Скорость центра масс стержня
Скорость центра масс стержня![]() где
где![]() МЦС стержня.
Принимая во внимание, что
МЦС стержня.
Принимая во внимание, что![]()
![]() получаем
получаем
![]()
Ползуны движутся поступательно и, следовательно,
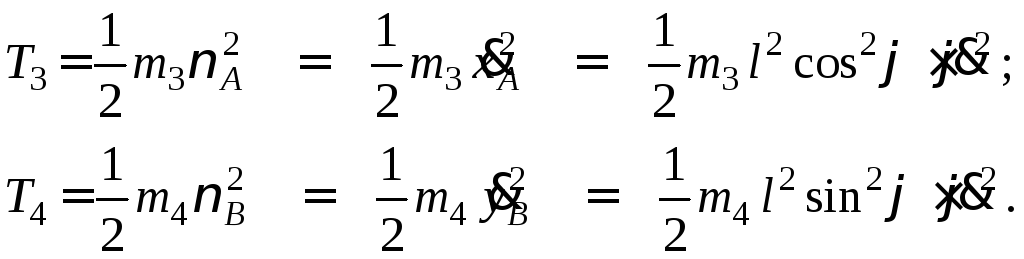
Таким образом, кинетическая энергия системы, выраженная через обобщенные координаты и обобщенные скорости, равна
T =

Вычисляем производные от кинетической энергии системы:
по q1 =
s
по q2
= 
 Для
нахождения обобщенных сил
Для
нахождения обобщенных сил![]() и
и![]() ,
соответствующих обобщенным координатам,
воспользуемся выражением виртуальной
работы сил (2.27), а именно:
,
соответствующих обобщенным координатам,
воспользуемся выражением виртуальной
работы сил (2.27), а именно:

В нашем случае:
 (2.27)
(2.27)
Эта формула позволяет вычислять обобщенные силы последовательно, учитывая, что обобщенные координаты , а значит, и их вариации независимы между собой. Поэтому системе можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются.
В нашем случае, сначала найдем виртуальную работу :
![]() ,
при
,
при![]()
![]()
![]()
 (2.43)
(2.43)
где
![]() а выражение в квадратных скобках в
уравнении виртуальной работы (2.43 перед
вариацией
а выражение в квадратных скобках в
уравнении виртуальной работы (2.43 перед
вариацией![]() есть
обобщенная сила:
есть
обобщенная сила:
![]()
![]() (2.44
(2.44
Найдем виртуальную работу :
![]() ,
при
,
при![]()
![]()

(2.45
где
 Выражение
в квадратных скобках в уравнении
виртуальной работы (2.45) перед вариацией
Выражение
в квадратных скобках в уравнении
виртуальной работы (2.45) перед вариацией![]() есть
обобщенная сила:
есть
обобщенная сила:
![]() =
=![]() .
.
(2.46)
Подставляя значения производных от
кинетической энергии и выражения для
обобщенных сил
![]() (2.44) и
(2.44) и![]() (2.46) в уравнения (2.42), получаем
дифференциальные уравнения движения
системы
(2.46) в уравнения (2.42), получаем
дифференциальные уравнения движения
системы
1) по q1
= s ![]()
2) по q2
=
 =
=
=
![]()
В о п р о с ы для с а м о ко н т р о л я
1. Дайте определение свободной и несвободной механической системы.
2. Несвободное движение системы. Аналитическое выражение связей и их классификация. Примеры.
3. Для какого уравнения связей излагается дальнейшая теория
составления уравнений движения несвободной механической системы?
Дайте определение возможных и виртуальных перемещений.
Приведите примеры. Направление виртуального перемещения.
Дайте определение обобщенных координат механической системы.
Каково число независимых координат, однозначно определяющих положение механической системы, состоящей и nматериальных точек?
Чему равно число степеней свободы механической системы, на которую наложены hуравнений ограничений?
Имеют ли обобщенные координаты начало отсчета и направление?
Приведите примеры, доказывающие, что обобщенные координаты независимые друг от друга параметры (неявные функции времени.).
Несвободное движение системы материальных точек или тел.
Дайте определение виртуальной работы. Идеальные связи.
От каких сил вычисляется виртуальная работа?
Четыре формулы определения виртуальной работы, по аналогии с формулами элементарной работы.
Как выражается сумма виртуальных работ сил системы через обобщенные силы? Приведите формулу.
Как определяется обобщенная сила? Какова ее ее размерность?
Способы нахождения обобщенных сил.
Как обобщенная сила зависит от силовой функции в случае действия на систему потенциальных сил?
Каков вид имеют уравнения Лагранжа второго рода? Чему
равно число этих уравнений для данной механической системы?
19. Написать формулы кинетических энергий для точки, системы точек, твердого тела в зависимости от вида его движения (при поступательном, вращательном вокруг неподвижной оси и точки, при плоском движении и в общем случае его движения).
Какой вид принимают уравнения Лагранжа второго рода для
механической системы, на которую действуют только потенциальные силы?
Какова последовательность действий при использовании
уравнений Лагранжа второго рода для решения задач о движении голономных систем с несколькими степенями свободы?
Глава3
ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ
НЕПОДВИЖНОЙ ТОЧКИ
3.1. Выбор осей координат. Углы Крылова.
Кинематические уравнения вращения
Вращательным движением твердого тела вокруг неподвижной точки называется такое его движение, при котором одна точка твердого тела или неизменно связанная с твердым телом , остается неподвижной относительно выбранной системы отсчета. Его еще называют сферическим движением, поскольку траектория любой точки тела лежит на поверхности сферы с центром в неподвижной точке. Примером такого движения служит волчок, у которого остается неподвижной точка опоры.
В главе 2 говорилось о том, что число
степеней свободы свободно движущегося
в пространстве твердого тела равно
шести. Если во время движения тела одна
его точка остается неподвижной, то число
степеней свободы такого тела при его
вращении вокруг этой неподвижной точки
будет равно трем, и для оценки его
положения необходимо задать три
главе 2 говорилось о том, что число
степеней свободы свободно движущегося
в пространстве твердого тела равно
шести. Если во время движения тела одна
его точка остается неподвижной, то число
степеней свободы такого тела при его
вращении вокруг этой неподвижной точки
будет равно трем, и для оценки его
положения необходимо задать три
Рис.3.1,а независимых параметра. Сделать это можно различными способами. Например, Крылов А.Н. в качестве таких параметров предложил так называемые корабельные углы, определяющие положение тела (корабля) относительно системы координат, связанной своим началом с его центром тяжести (рис.3.1,б).
За оси неподвижной системы координат
приняты CXYZ,а за
оси жестко связанные с кораблем
Cxyz(рис.3.1). ОсьСХнаправлена от кормы к носу корабля, осьCZ
к его правому борту, а ось CY
образует с ними правую систему
координат.(вертикально вверх). Положение
подвижной системы координат Cxyz,
неизменно связанной с кораблем,
относительно неподвижной
CXYZ для каждого
момента времени определяется тремя
углами Крылова:
![]() угол дифферента,
угол дифферента, ![]() угол
крена,
угол
крена,
![]() угол
рыскания.
угол
рыскания.

Рис.3.1,б
Как видно на рис.3.1,а плоскость CXY
пересекает плоскостьCxy
по некоторой прямой
![]() ,
образующей угол
,
образующей угол
![]() с
осью CXи угол
с
осью CXи угол
![]() с осьюCx. ПлоскостьCYZ пересекает
плоскостьCX y
по линии
с осьюCx. ПлоскостьCYZ пересекает
плоскостьCX y
по линии
![]() ,
образующей угол
,
образующей угол![]() с осьюCy.
с осьюCy.
Рассмотрим переход от системы CXYZк системеCxyz, выполненный с помощью трех поворотов.
Для совмещения системы CXYZс системойCxyzдостаточно:
1) повернуть систему CXYZ
вокруг третьей из координатных осейCZнаугол дифферента
![]() ,
в результате чего получаем систему
,
в результате чего получаем систему![]() ,
причем
,
причем![]() ;
;
2) повернуть систему
![]() вокруг первой из координатных осей
вокруг первой из координатных осей![]() наугол крена
наугол крена
![]() ,
в результате чего имеем систему
,
в результате чего имеем систему![]() ,
при этом
,
при этом![]() ;
;


Рис.3.2 Рис.3.3
3) повернуть систему
![]() вокруг второй из координатных осей
вокруг второй из координатных осей![]() науголрыскания,
в результате чего приходим к системеCxyz .
науголрыскания,
в результате чего приходим к системеCxyz .
1. Координаты систем CXYZи![]() ,
как видно из рис.3.2, связаны соотношениями
,
как видно из рис.3.2, связаны соотношениями
X=x(1) cos y(1) sin + 0 ,
Y = x(1) sin + y(1) cos + 0 , (3.1)
Z= 0 + 0 +z(1) ,
или в матричной форме:
[X] ={3}т[x(1)]
или (3.2)
(3.2)
![]()
матрица, транспонированная к матрице
матрица, транспонированная к матрице![]() ,
описывающей поворот системыCXYZвокруг третьей координатной осиСZна угол дифферента:
,
описывающей поворот системыCXYZвокруг третьей координатной осиСZна угол дифферента:
{3}
т=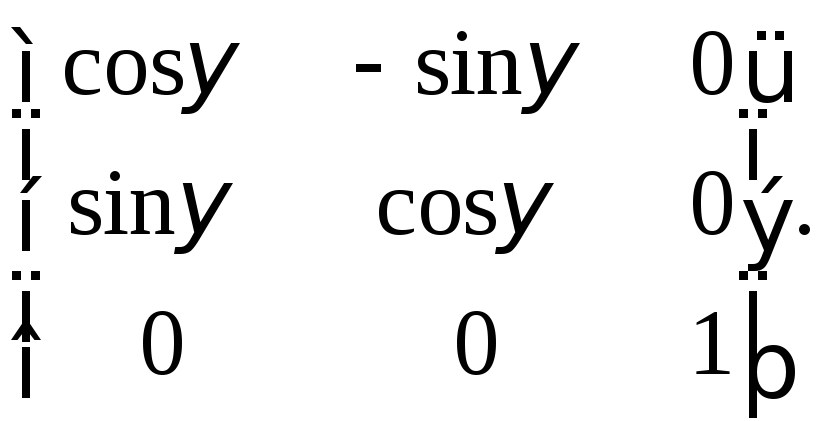 (3.3)
(3.3)
2. Переход от системы
![]() к системе
к системе![]() происходит путем поворота наугол
крена
происходит путем поворота наугол
крена
![]() вокруг первой из координатных осей
вокруг первой из координатных осей![]() ,
при этом
,
при этом![]() .
.
Формулы преобразования координат, как видно из рис.3.3, при этом таковы:
x(1) = x(2) + 0 + 0 ,
y(1)
= 0 + y
(2) cos
![]()
z
(2) sin
z
(2) sin
![]() , (3.4)
, (3.4)
z
(1)= 0 +y(2)sin
![]() + z
(2)cos
+ z
(2)cos
![]() ,
,
или в матричной форме
[x(1)] =![]() [x(2)], или
[x(2)], или (3.5)
(3.5)
где
![]() матрица, транспонированная к матрице
матрица, транспонированная к матрице![]() ,
задающей преобразование поворота от
осей системы
,
задающей преобразование поворота от
осей системы![]() к осям системы
к осям системы![]() вокруг
первой из координатных осей
вокруг
первой из координатных осей![]() наугол крена
наугол крена
![]() ,
при этом
,
при этом![]() .
.
 (3.6)
(3.6)
3.Наконец, система координат
![]() переводится в системуCxyz
поворотом науголрысканиявокруг второй из координатных осей
переводится в системуCxyz
поворотом науголрысканиявокруг второй из координатных осей
![]() ,
и поэтому формулы преобразования
координат, как видно на рис.3.4, имеют
вид:
,
и поэтому формулы преобразования
координат, как видно на рис.3.4, имеют
вид:
 x(2)
= x cos
+ 0 +z sin
,
x(2)
= x cos
+ 0 +z sin
,
y(2) = 0 + y + 0 , (3.7)
z(2)=xsin+ 0 +z cos,
или в матричной форме: [x(2)]=![]() или
или
 (3.8)
(3.8)
Рис.3.4
Причем поворотная матрица {2
}тматрица,
транспонированная к матрице {2
}, задающей преобразование поворота
от осей системы![]() к осям системыCxyzнауголрыскания
вокруг второй из координатных осей
к осям системыCxyzнауголрыскания
вокруг второй из координатных осей![]() ,
имеет вид :
,
имеет вид :
{
2}т
= (3.9)
(3.9)
Для любой точки Мтела с координатамиx, y, zв подвижной
системе координат, жестко связанной с
ним, и с ее же координатамиX, Y ,Z в
неподвижной системе координат можно
установить взаимосвязь проекций вектора
точки![]() на
оси двух систем координат,
на
оси двух систем координат,
![]() (3.10)
(3.10)
или в матричном виде
![]()
![]() или
или
 (3.11)
(3.11)
где
углы Крылова являются некоторыми
функциями времени:
дифферента ![]() =
=![]() ,
крена
,
крена ![]() =
=![]() ;
рыскания
;
рыскания ![]() =
=![]() ,
,
![]()
матрица, транспонированная к матрице
направляющих косинусов
матрица, транспонированная к матрице
направляющих косинусов![]() ,
задающей преобразование поворота от
осей неподвижной системы CXYZ
к осям подвижной системыCxyz,
неизменно связанной с кораблем. Очевидно,
что при движении тела координатыx, y,
zостаются постоянными в отличие от
координатX, Y,
Z.
,
задающей преобразование поворота от
осей неподвижной системы CXYZ
к осям подвижной системыCxyz,
неизменно связанной с кораблем. Очевидно,
что при движении тела координатыx, y,
zостаются постоянными в отличие от
координатX, Y,
Z.
Подставляя в соотношение (3.2): [X]
={3}т[x(1)]
соотношение (3.5): [x(1)]
=![]() т[x(2)] , в котором
[x(2)] = {2
}т[x]
т[x(2)] , в котором
[x(2)] = {2
}т[x]
представлено в виде (3.8), получаем
![]() (3.12)
(3.12)
Сравнивая выражения (3.11) и (3.12), находим, что искомая матрица
![]() является
произведением трех матриц поворота:
является
произведением трех матриц поворота:
![]() =
=![]()
=  =
=
=
= (3.13)
(3.13)
Подставляя в соотношение (3.2): [X]
={3}т[x(1)]
соотношение (3.5): [x(1)]
=![]() т[x(2)], получаем
промежуточные соотношения, которые
могут понадобиться в дальнейшем,
т[x(2)], получаем
промежуточные соотношения, которые
могут понадобиться в дальнейшем,
[X] ={3}т
![]() т[x(2)].
т[x(2)].
Промежуточная поворотная матрица
![]() = {3}т
= {3}т![]() т
находится как произведение двух
матриц поворота, а именно:
т
находится как произведение двух
матриц поворота, а именно:
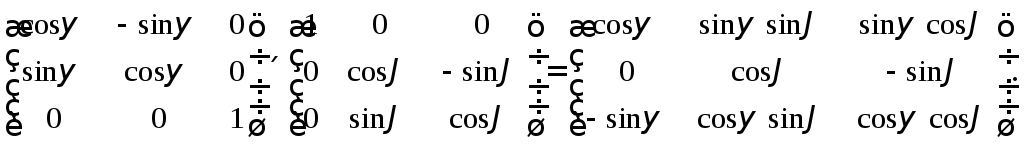 (3.13*)
(3.13*)
