
- •Введение
- •Некоторые сведения о методиках динамического расчета артиллерийских орудий
- •Глава 1 математическая модель действия выстрела на артиллерийское орудие
- •1.1. Выбор и обоснование расчетной схемы
- •1.2 Анализ конструкций современных образцов артиллерийских орудий
- •Глава 2
- •Движение при наличии связей.
- •Уравнения лагранжа второго рода при нестационарном базисе
- •Основные понятия
- •2.1. Несвободное движение точки.
- •2.2 Связи и их классификация
- •2.3.Возможные и виртуальные перемещения
- •2.4 Обобщенные координаты. Число степеней свободы механической системы
- •В различных случаях
- •2.5. Несвободное движение системы материальных точек
- •2.6. Виртуальная работа силы. Идеальные связи
- •2.7. Обобщенные силы
- •2.8. Уравнения Лагранжа второго рода
- •2.9. Последовательность действий при использовании уравнений Лагранжа второго рода для решения задач о движении голономных систем с несколькими степенями свободы
- •Движении:
- •3.2. Углы Эйлера.
- •3.3.Формулы преобразования координат. Поворотные матрицы
- •3.4. Мгновенная угловая скорость и угловое ускорение Кинематические уравнения Эйлера
- •3.5. Скорость и ускорение точек тела. Формула Ривальса
- •Расчетная работа № 1 – Тема: кинематика вращения твердого тела вокруг неподвижной точки случай регулярной прецессии
- •4.1. Схемы конструкций и таблица к ним с исходными данными к расчетной работе «№1»
- •4.2.Методические указания и план решения расчетной работы № 1
- •4.3. Пример 4.1решения расчетной работы № 1 (рис.4.3). Тема: вращение твердого тела вокруг неподвижной точки
- •4.4. Пример 4.2 решения расчетной работы №1 (рис.4.4). Тема: вращение твердого тела вокруг неподвижной точки
- •5.2. Пример 5.1 выполнения второй расчетной работы №2
- •Курсовая работа тема:
- •Расчет динамических моделей объектов вооружения
- •Конкретных конструктивно компоновочных схем по учебной дисциплине «динамика конструкций»
- •.Методические указания и примеры выполнения
- •Пример 6.2 выполнения расчетной работы по динамике несвободной механической системы с тремя степенями свободы (рис.6.3.1)
- •Окончательный вид уравнений Лагранжа второго рода или дифференциальные уравнения движения рассматриваемой системы в обобщенных координатах
- •Пример 6.3 выполнения расчетной работы по динамике несвободной механической системы с тремя степенями свободы
- •Литература Основная литература
- •Дополнительная литература
- •Глава 3. Вращение твердого тела вокруг неподвижной точки .44
- •Глава 4. Расчетная работа № 1–тема: вращение твердого
3.2. Углы Эйлера.
Формулы преобразования координат. Поворотные матрицы
В тех случаях, когда угловая скорость вращения в одном направлении значительно больше угловых скоростей вращения в двух других направлениях ( генераторы, моторы, турбины, гироскопы), для определения положения тела в качестве трех независимых параметра выбирают три угла Эйлера: угол прецессии , угол нутации , и угол ротации ( собственного вращения) .Название этих углов заимствованы из астрономии.
Чтобы задать эти углы, рассмотрим вращение твердого тела вокруг неподвижной точки О. Пусть даны некоторая система отсчета и связанная с ней неподвижная система координат0XYZ, относительно которой движется твердое тело, и связанная с твердым телом система координат0xyz, которая движется относительно первой (рис.3.5). Это означает, что первая и вторая системы координат имеют общее началоO, а углы, образуемые осями0xyzс осями0XYZ, изменяются, т.е. система0XYZ
 поворачивается
вместе с твердым телом вокруг неподвижной
точки 0 (рис.3.5).
поворачивается
вместе с твердым телом вокруг неподвижной
точки 0 (рис.3.5).
На рис.3.5 видно, что плоскость 0XY(изображена в виде заштрихованного
овала) пересекает плоскость0xy(изображена белым овалом) по некоторой
прямой0z(1)
=0z(2) =OE, образующей уголс неподвижной осью0Zи уголс подвижной осью0z,
которая называетсялинией узлов
0Ес единичным ортом
![]() .
Кроме того, плоскость0xyобразует с плоскостью0XYугол ,
равный углу между осями 0Yи 0y.
.
Кроме того, плоскость0xyобразует с плоскостью0XYугол ,
равный углу между осями 0Yи 0y.
Рис.3.5,а
Неподвижная ось ОY,
вокруг которой поворачивается
твердое тело наугол прецессии
,
называется осью прецессиис единичным
ортом![]() .
.
Изменение угла нутации сопровождается вращением твердого тела вокруглинии узлов0z(1) =0z(2) =OE, называемойосью нутации.
Наконец, угол ротации (собственного
вращения)
характеризует вращение тела вокруг осиOy=Oy(2),
называемойосью ротации (собственного
вращения)с единичным ортом![]() .
.

Рис. 3.5,б
На рис 3.5,а3.5,б показаны все углы положительными, т.е. против хода часовой стрелки, если смотреть на поворот тела с положительных направлений осей вращенияOY, OE и Oyсоответственно.
Если заданы уравнения вращения
твердого тела вокруг неподвижной точки
О, а именно:угол прецессии![]() =
=![]() ,угол нутации
,угол нутации ![]() =
=![]() и угол ротации
(собственного вращения )
и угол ротации
(собственного вращения )
![]() =
=![]() ,то положение твердого тела
полностью определяется положением
подвижной связанной с твердым телом
системы координат0xyz
относительно неподвижной системы
координат0XYZдля
любого момента времени..
,то положение твердого тела
полностью определяется положением
подвижной связанной с твердым телом
системы координат0xyz
относительно неподвижной системы
координат0XYZдля
любого момента времени..
3.3.Формулы преобразования координат. Поворотные матрицы
Для любой точки Мтела с координатамиx, y, z в подвижной
системе координатОxyz, жестко
связанной с ним, и с ее же координатамиX, Y ,Zв неподвижной
системе координат0XYZв соответствии с (3.10), взаимосвязь
проекций вектора точки![]() на
оси двух систем координат [X]Ни [x]Пимеет вид:
на
оси двух систем координат [X]Ни [x]Пимеет вид:
![]() (3.14)
(3.14)
и ли
в матричном виде
ли
в матричном виде![]()
![]() или
или
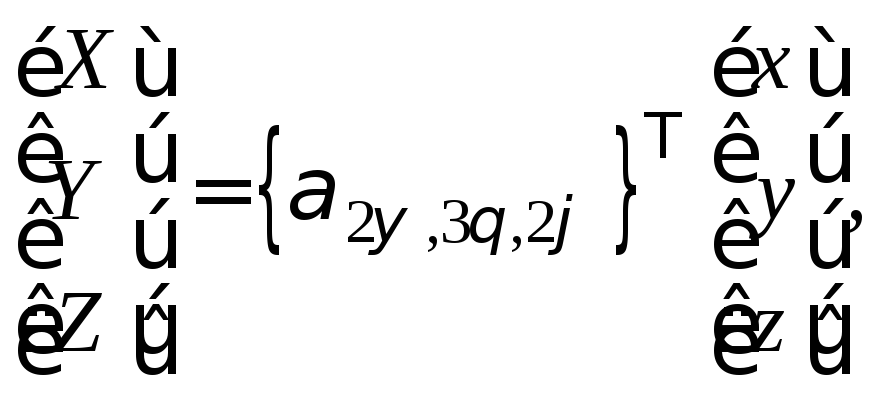 (3.15)
(3.15)
где
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]()
углы
Эйлера ;
углы
Эйлера ;
Рис.3.6 ![]()
матрица,
матрица,
транспонированная
к матрице направляющих косинусов
![]() ,
задающей преобразование поворота от
осей неподвижной системы
OXYZ
(с
базисом [X]Н
)
к осям подвижной системы Оxyz
(с базисом [x]П),
неизменно связанной с телом.
Транспонированная матрица
,
задающей преобразование поворота от
осей неподвижной системы
OXYZ
(с
базисом [X]Н
)
к осям подвижной системы Оxyz
(с базисом [x]П),
неизменно связанной с телом.
Транспонированная матрица ![]() получается
путем замены в матрице
получается
путем замены в матрице

Рис.3.7
![]() строк
на столбцы. Выражение
строк
на столбцы. Выражение
![]() получается
в результате рассмотрения формул
преобразований координат при переходе
от одной системы к другой: [X]Н)
[x](1)
[x](2)
[x]П
,
из которых две системы [x]
(1)
и [x]
(2) -
промежуточные.
получается
в результате рассмотрения формул
преобразований координат при переходе
от одной системы к другой: [X]Н)
[x](1)
[x](2)
[x]П
,
из которых две системы [x]
(1)
и [x]
(2) -
промежуточные.
1. Переход от осей системы [X]Нк осям системы [x]
(1) осуществляется поворотом на
уголпрецессии
![]() вокруг неподвижной осиOY
прецессии
системы [X]Н(рис.3.63.8,а).
вокруг неподвижной осиOY
прецессии
системы [X]Н(рис.3.63.8,а).
2. Переход от осей системы [x]
(1)к осям системы [x]
(2) осуществляется поворотом наугол нутации ![]() вокруг оси
вокруг оси![]() системы
[x] (1) (рис.3.63.8,б).
системы
[x] (1) (рис.3.63.8,б).
3. Переход от осей системы [x]
(2)к осям системы [x]П
-поворотом наугол ротации (собственного вращения )
![]() вокруг оси
вокруг оси![]() системы
[x] (2).
системы
[x] (2).

Рис.3.8
Рассмотрев переход от системы ОXYZ ([X]Н) к системеОxyz ([x]П ), выполненный с помощью трех поворотов, получаем следующие формулы для преобразования координат:
1) поворот системы ОXYZвокруг второй из координатных осейОYнаугол прецессии![]() ,
т.е. [X]Н
[x]1), ОXYZ
,
т.е. [X]Н
[x]1), ОXYZ
![]() ,
причем
,
причем![]() (рис.3.63.8,а).
(рис.3.63.8,а).
Координаты систем координат 0XYZи 0x(1)y(1)z(1), как видно на рис.3.8,a, связаны соотношениями
X= x(1) cos + 0 + z(1) sin ,
Y = 0 + y(1) + 0 ,
Z=x(1)sin+ 0 +z(1) cos,
или в матричной форме:
[X] ={2} т[x(1)], (3.16)
где матрица {2}
т= . (3.17)
. (3.17)
описывает поворот вокруг второй оси
0Yна угол прецессии
![]() .
.
2) поворот системы
![]() вокруг третьей из координатных осей
вокруг третьей из координатных осей![]() наугол нутации
наугол нутации ![]() ,
т.е. [x]1) [x](2)
,
,
т.е. [x]1) [x](2)
,![]()
![]() ,
при этом
,
при этом![]() (рис.3.63.8,б).
(рис.3.63.8,б).
Формулы преобразования координат, как видно на рис.3.8,.б, при этом таковы:
x(1) = x(2) cos y (2) sin + 0 ,
y(1) = x(2) sin + y (2) cos + 0 ,
z (1)= 0 + 0 +z (1),
или в матричной форме:
[x(1)] = {3 } т[x(2)], (3.18)
где матрица {3
} т= .
(3.19)
.
(3.19)
описывает поворот вокруг оси 0z(1)на угол нутации.
3) поворот системы
![]() вокруг второй из координатных осей
вокруг второй из координатных осей![]() наугол ротации
(собственного вращения )
наугол ротации
(собственного вращения )
![]() ,т.е.. [x](2)
[x]П
, (рис.3.63.8,а)
,т.е.. [x](2)
[x]П
, (рис.3.63.8,а)![]() Cxyz,
поэтому формулы преобразования
координат, как видно из рис.3.8,а,
имеют вид:
Cxyz,
поэтому формулы преобразования
координат, как видно из рис.3.8,а,
имеют вид:
x(2) = x cos + 0 + z sin ,
y(2) = 0 +y + 0 ,
z(2)=xsin+ 0 +z cos,
или в матричной форме:
[x(2)] = {2 }т[x], (3.20)
поворотная матрица { 2 }т имеет вид матрицы (4.17){2} т,
{2}
т= .
(3.21)
.
(3.21)
Подставляя в соотношение (3.16) [X] ={2} т[x(1)] соотношение (3.18)[x(1)] = = {3 } т[x(2)], получаем промежуточные соотношения, которые могут понадобиться в дальнейшем, а именно:
[X] ={2} т{3} т[x(2)] или (3.22)
Промежуточная поворотная матрица {2,3 }тнаходится как произведение двух матриц поворота, а именно:
{ 2,3 }т= {2}т{3 } т= (3.23
=
 =
=

Подставляя в соотношение (3.16) [X] ={2} т[x(1)] соотношение (3.18)[x(1)] = = {3 } т[x(2)], в котором [x(2)] представлено в виде (3.20)[x(2)]= {2 }т[x], получаем
[X] ={2} т{3} т{2 }т[x]. (3.24)
Сравнивая выражения (3.15) ![]() и (3.24), находим, что искомая поворотная
матрица
и (3.24), находим, что искомая поворотная
матрица![]() является произведением трех матриц
поворота (3.17), (3.19), (3.21), а именно:
является произведением трех матриц
поворота (3.17), (3.19), (3.21), а именно:
{ ,,
} т=![]() =
{2}
т{3
} т{2
} т=
=
{2}
т{3
} т{2
} т=
=

 =
=

(3.25)
При заданном законе сферического движения выражения (3.15) и (3.25) позволяют определить искомый закон движения и траекторию выбранной точки тела.
