Окончательный вид уравнений Лагранжа второго рода или дифференциальные уравнения движения рассматриваемой системы в обобщенных координатах

где

;

где ;

где

,или матричная форма уравнений Лагранжа

,

где инерционная матрица, где

;

матрица-столбец обобщенных ускорений;



матрица-столбец обобщенных сил;

матрица-столбец слагаемых, перенесенных из левых частей уравнений Лагранжа, не содержащих обобщенных ускорений.

Решение уравнений Лагранжа второго рода на интервале времени от t=0 с до t=0,01 с выполнено в системе Mathcad 11. Распечатка программы расчёта в системе Mathcad 11 для начального угла ц₀ = 30° приведёна на рис. 6.2.36.2.7. Распечатка программы расчёта в системе Mathcad 11 для начального угла ц₀ = 6° приведёна на рис.6.3.3 и 6.3.8.

Пример 6.3 выполнения расчетной работы по динамике несвободной механической системы с тремя степенями свободы

Рис.6.3.2

Рис. 6.3.2. Полый цилиндр 2 массой m₂ скользит по основанию 1 массой m₁, опирающемуся на цилиндрический шарнир О и поддерживаемому вертикальной пружиной КМ. Жесткость пружины C₁, длина недеформированной пружины l₂, расстояние от шарнира О до точки К опоры пружины l₁. Коэффициент трения цилиндра об основание f = 0,12. K шарниру C прикреплена горизонтальная пружина CD жесткостью C₂. В начальном положении пружина CD не деформирована, а пружина КМ поддерживает систему в положении статического равновесия.

Введем неподвижную систему координат OXYZ, ось OX которой горизонтальна, и связанную с основанием систему координат OX₁Y₁Z₁, ее ось OX₁ параллельна направляющей основания, по которой скользит цилиндр. Положение центра масс O₁ основания задается координатами x_1O и y_1O точки O₁ в системе координат OX₁Y₁Z₁, причем y_1O = 0,6 м. Начальное положение цилиндра на основании определяется заданием начальных значений координат x_2O и y_2O точки O₂ в системе координат OX₁Y₁Z₁. Точка O_н совпадает с начальным положением центра масс цилиндра O₂.

В начальный момент времени к внутренней поверхности дна цилиндра прикладывается переменная нагрузка P(t), определяемая зависимостью (6.1). При этом цилиндр 2 начинает скользить по основанию 1, вызывая вращение последнего вокруг оси шарнира OZ. Движение цилиндра тормозится реакцией R(t) тормозного устройства 3, приложенной к внешней поверхности дна цилиндра. Величина реакции определяется формулой (6.2). Моменты инерции основания 1 и цилиндра 2 относительно осей O₁z и O₂Z₂ равны J₁ и J₂, соответственно.

Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.

Указание. В качестве обобщенных координат выбрать :

перемещение точки C по горизонтальной оси , отсчитанное от положения статического равновесия пружиныCD.

угол поворота  основания 1 , отсчитанный от горизонтали и

перемещение  S центра масс 2 цилиндра 2 по направляющей основания 1 , отсчитанную от его начального положенияO_н. Начальное значение  = ₀. Длину недеформированной пружины l₂ определить из условия статического равновесия системы в начальный момент времени. Рекомендуемые значения величин приведены в таблице 6.3.

Исходные данные:

m₁ – масса цилиндра;

m₂ – масса направляющих.

Число степеней свободы: i = s = 3

За обобщенные координаты приняты следующие параметры:

_;

Обобщенные скорости:

Что входит в рассматриваемую механическую систему:

основание (1) и цилиндр (2) совершают плоско-параллельное движение относительно неподвижной системы координат OXYZ

, где

; ;

Координаты центра массы основания 1 в матричной форме:

(1), или

, где , т.е.

;

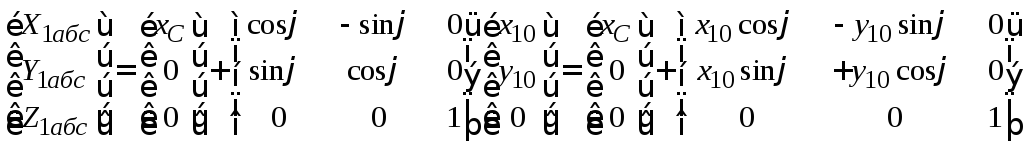Скорости центра массы основания 1 в матричной форме:

; или

.

Кинетическая энергия основания 1 в функции обобщенных координат и обобщенных скоростей:

Координаты центра массы цилиндра 2 в матричной форме:

Скорости центра массы цилиндра 2 в матричной форме:

их квадраты:

Кинетическая энергия цилиндра 2 в функции обобщенных координат и обобщенных скоростей:

Кинетическая энергия системы

Уравнения Лагранжа второго рода для данной системы:

I уравнение: по

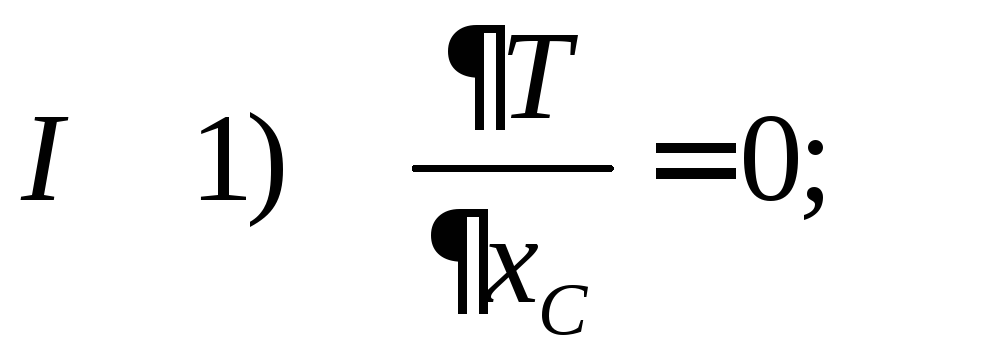
I

II уравнение: по

II

III

Запишем окончательно уравнения Лагранжа, второго рода, оставив в левой части только слагаемые со вторыми производными от обобщенных координат. Все остальные слагаемые перенесем в правую часть уравнения, обозначив их как:

Уравнения Лагранжа Второго рода в матричной форме:

,

где инерционная матрица, где

или

где: инерционные коэффициенты:

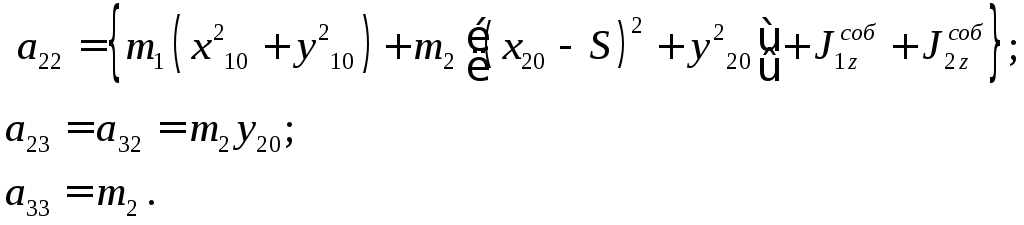
Виртуальная работа сил, действующих на рассматриваемую систему: (5);

(5_*)

Так как обобщённые координаты независимые друг от друга параметры, то и их вариации тоже независимые. Поэтому, используя принцип замораживания, находим виртуальные работы, соответствующие виртуальным перемещениям поочередно.

1) ,

,

2)

3),

Сравнивая множители в соответствующих формулах виртуальных работ(1, 2, 3) перед вариациями соответствующих обобщённых координат и в формуле (5*), находим обобщённые силы, соответствующие обобщённым координатам.