- •Глава 3. Производная функции одной переменной
- •3.1. Производная функции в точке
- •X Физический смысл производной
- •Геометрический смысл производной. Связь с существованием касательной
- •Уравнения касательной и нормали
- •Бесконечные производные
- •Односторонние производные
- •3.2. Дифференцируемость функции одной переменной Определение функции, дифференцируемой в точке
- •Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
- •Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
- •3.3. Правила вычисления производных
- •3.6. Производные некоторых элементарных функций (таблица производных)
- •3.7. Логарифмическая производная
- •3.8. Производная функции, заданной параметрически
- •3.9. Дифференцирование функций, заданных неявно
- •Глава 4. Производные и дифференциалы высших порядков
- •4.1. Дифференциал функции одной переменной
- •Геометрический смысл дифференциала
- •Инвариантность формы дифференциала первого порядка
- •Дифференциал и приближенные вычисления
- •4.2. Производные и дифференциалы высших порядков Понятие производной - го порядка
- •Дифференциалы высших порядков
- •Правила вычисления производной суммы - го порядка. Формула Лейбница для- й производной произведения двух функций
- •4.3. Теоремы о непрерывных и дифференцируемых функциях
- •4.4. Формулы конечных приращений, их приложения
- •Теорема Ролля5о среднем
- •4.5. Раскрытие неопределенностей (Правило Лопиталя)
- •4.6. Формула Тейлора для многочленов
- •4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано10
- •4.8. Формула Тейлора с остаточным членом в форме Лагранжа
- •Формула Маклорена11
- •4.9. Разложения основных элементарных функций (асимптотические формулы)
- •Глава 5. Исследование и построение графиков функции одной переменной
- •5.1. Условия возрастания и убывания функции
- •5.2. Локальный экстремум Теорема 5.2 (первое достаточное условие локального экстремума дифференцируемой функции)
- •5.3. Абсолютный экстремум функции
- •5.4. Выпуклость и точки перегиба графика функции
- •Точки перегиба графика функции
- •5.5. Асимптоты графика функции
- •5.6. Схема исследования функций и построения кривых
3.8. Производная функции, заданной параметрически
Пусть
зависимость между аргументом
 и функцией
и функцией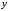 задана при помощи уравнений
задана при помощи уравнений
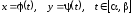 , (3.10)
, (3.10)
где
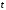 – вспомогательная
переменная, называемая параметром.
– вспомогательная
переменная, называемая параметром.
Пусть
для функция
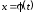 существует обратная функция
существует обратная функция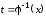 .
Тогда равенства (3.10) определяют сложную
функцию
.
Тогда равенства (3.10) определяют сложную
функцию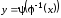 аргумента
аргумента ,
заданную параметрически уравнениями
(3.10). Найдем ее производную, используя
теоремы о дифференцировании сложной и
обратной функций:
,
заданную параметрически уравнениями
(3.10). Найдем ее производную, используя
теоремы о дифференцировании сложной и
обратной функций:
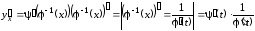 .
.
Здесь
производная
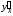 выражена через
параметр
выражена через
параметр
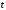 .
Чтобы установить ее связь с переменной
.
Чтобы установить ее связь с переменной ,
нужно
использовать уравнение
,
нужно
использовать уравнение
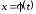 .
Т. о., если функция задана параметрически,
то и ее производная задана параметрически:
.
Т. о., если функция задана параметрически,
то и ее производная задана параметрически:
функция:
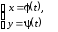
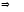 ее
производная:
ее
производная: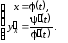
Если
при этом функции
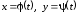 дважды
дифференцируемы на
дважды
дифференцируемы на
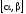 ,
то существует производная второго
порядка
,
то существует производная второго
порядка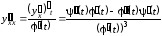 ,
выраженная через параметр
,
выраженная через параметр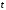 .
Но нет смысла запоминать последнюю
формулу, так как указанный метод можно
применять столько раз, сколько потребуется.
.
Но нет смысла запоминать последнюю
формулу, так как указанный метод можно
применять столько раз, сколько потребуется.
Пример
3.10. Найти
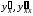 для функции
для функции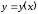 ,
заданной параметрическими уравнениями
,
заданной параметрическими уравнениями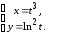
Решение.
Первая производная
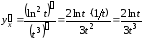 .
Вторая производная
.
Вторая производная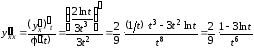 .
.
3.9. Дифференцирование функций, заданных неявно
Пусть
функция
 задана в неявном виде, т. е. уравнением,
не разрешенным относительно
задана в неявном виде, т. е. уравнением,
не разрешенным относительно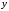 ,
,
 .
.
Если
функция
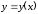 дифференцируема на
дифференцируема на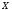 ,
то можно вычислить производную
,
то можно вычислить производную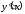 ,
не зная в явном виде формулы, задающей
,
не зная в явном виде формулы, задающей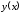 .
Для этого тождество
.
Для этого тождество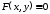 нужно продифференцировать по переменной
нужно продифференцировать по переменной ,
считая при этом
,
считая при этом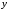 функцией от
функцией от .
Получим равенство, которое вместе с
соотношением
.
Получим равенство, которое вместе с
соотношением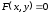 неявно определяет производную
неявно определяет производную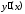 .
.
Пример
3.11. Найти
производную функции
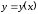 ,
заданной уравнением
,
заданной уравнением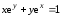 .
Вычислить значение
.
Вычислить значение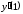 .
.
Решение.
Дифференцируем уравнение по переменной
 ,
считая при этом
,
считая при этом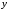 функцией от
функцией от :
:
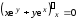 .
.
Пользуемся
правилами дифференцирования сложной
функции и произведения функций:
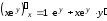 ,
,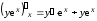 .
Тогда уравнение
принимает вид:
.
Тогда уравнение
принимает вид:
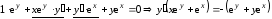 .
Отсюда
.
Отсюда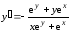 .
Но
.
Но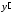 зависит не только от
зависит не только от ,
но и от
,
но и от
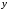 .
Чтобы найти
.
Чтобы найти
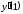 ,
сначала нужно найти
,
сначала нужно найти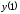 .
Подставим
.
Подставим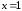 в исходное уравнение:
в исходное уравнение: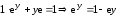 .
Так как в левой части уравнения
возрастающая функция, а в правой
убывающая, то
.
Так как в левой части уравнения
возрастающая функция, а в правой
убывающая, то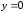 является единственным корнем этого
уравнения. Итак,
является единственным корнем этого
уравнения. Итак,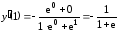 .
.
Глава 4. Производные и дифференциалы высших порядков
4.1. Дифференциал функции одной переменной
Пусть
функция
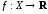 определена на множестве
определена на множестве
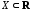 идифференцируема
в точке
идифференцируема
в точке
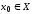 предельной для множества
предельной для множества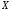 .
.
Определение.
Дифференциалом
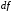 или
или
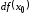 функции
функции
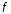 в точке
в точке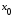 называется линейная функция приращения
называется линейная функция приращения :
:
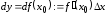 . (4.1)
. (4.1)
Формулу (4.1) приращения дифференцируемой функции можно записать в виде:
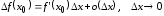 .
.
Заметим, что из последней формулы вытекает, что
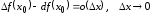 ,
,
т.
е. разность
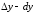 имеет более высокий порядок малости по
сравнению с
имеет более высокий порядок малости по
сравнению с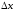 .
Поэтому говорят, что дифференциал естьглавная
часть
приращения функции
.
Поэтому говорят, что дифференциал естьглавная
часть
приращения функции
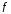 в точке
в точке .
.
Если
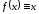 ,
то, очевидно,
,
то, очевидно,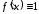 и
и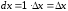 ,
то есть
,
то есть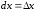 .
.
Поэтому
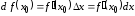
или
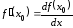 ,
,
то
есть отношение дифференциалов
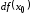 и
и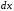 равно
равно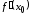 .
По этой причине, следуя Лейбницу,
производную частообозначают
символом
.
По этой причине, следуя Лейбницу,
производную частообозначают
символом
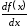 наряду с предложенным впоследствии
Лагранжем символом
наряду с предложенным впоследствии
Лагранжем символом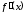 .
.
Геометрический смысл дифференциала
Посмотрим
на дифференциал с геометрической точки
зрения (рис. 4.1). На рисунке к графику
функции
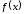 проведена
касательная в точке А
с абсциссой
проведена
касательная в точке А
с абсциссой
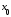 .
Согласно (4.1)
.
Согласно (4.1)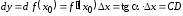 –приращение
ординаты касательной к графику функции
–приращение
ординаты касательной к графику функции в точке
в точке
 .
При этом разность
.
При этом разность
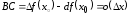 –бесконечно
малая более высокого порядка, чем
–бесконечно
малая более высокого порядка, чем
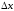 .
.