
- •Глава 3. Производная функции одной переменной
- •3.1. Производная функции в точке
- •X Физический смысл производной
- •Геометрический смысл производной. Связь с существованием касательной
- •Уравнения касательной и нормали
- •Бесконечные производные
- •Односторонние производные
- •3.2. Дифференцируемость функции одной переменной Определение функции, дифференцируемой в точке
- •Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
- •Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
- •3.3. Правила вычисления производных
- •3.6. Производные некоторых элементарных функций (таблица производных)
- •3.7. Логарифмическая производная
- •3.8. Производная функции, заданной параметрически
- •3.9. Дифференцирование функций, заданных неявно
- •Глава 4. Производные и дифференциалы высших порядков
- •4.1. Дифференциал функции одной переменной
- •Геометрический смысл дифференциала
- •Инвариантность формы дифференциала первого порядка
- •Дифференциал и приближенные вычисления
- •4.2. Производные и дифференциалы высших порядков Понятие производной - го порядка
- •Дифференциалы высших порядков
- •Правила вычисления производной суммы - го порядка. Формула Лейбница для- й производной произведения двух функций
- •4.3. Теоремы о непрерывных и дифференцируемых функциях
- •4.4. Формулы конечных приращений, их приложения
- •Теорема Ролля5о среднем
- •4.5. Раскрытие неопределенностей (Правило Лопиталя)
- •4.6. Формула Тейлора для многочленов
- •4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано10
- •4.8. Формула Тейлора с остаточным членом в форме Лагранжа
- •Формула Маклорена11
- •4.9. Разложения основных элементарных функций (асимптотические формулы)
- •Глава 5. Исследование и построение графиков функции одной переменной
- •5.1. Условия возрастания и убывания функции
- •5.2. Локальный экстремум Теорема 5.2 (первое достаточное условие локального экстремума дифференцируемой функции)
- •5.3. Абсолютный экстремум функции
- •5.4. Выпуклость и точки перегиба графика функции
- •Точки перегиба графика функции
- •5.5. Асимптоты графика функции
- •5.6. Схема исследования функций и построения кривых
4.5. Раскрытие неопределенностей (Правило Лопиталя)
Теорема о нахождении предела отношения функций через предел отношения производных
Пусть
функции
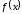 и
и
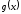 :
:
1)
определены и дифференцируемы в некоторой
проколотой окрестности точки
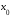 ;
;
2)
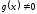 и
и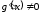 в
этой окрестности;
в
этой окрестности;
3)
существует
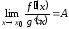 (конечный или бесконечный);
(конечный или бесконечный);
4)
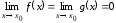 или
или .
.
Тогда
существует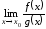 ,
причем
,
причем
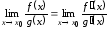 .
.
Замечание.
Правило Лопиталя можно рассматривать
и в случае
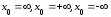 .
В этом случае достаточно сделать замену
.
В этом случае достаточно сделать замену и воспользоваться результатом теоремы.
и воспользоваться результатом теоремы.
Доказательство.
Рассмотрим
случай
 .
Доопределим функции
.
Доопределим функции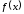 и
и
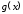 в точке
в точке
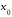 :
:
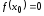 и
и .
Так как теперь
.
Так как теперь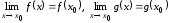 ,
то функции
,
то функции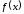 и
и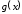 будут непрерывны в точке
будут непрерывны в точке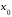 .
Поэтому на отрезке
.
Поэтому на отрезке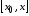 ,
где
,
где – любая точка окрестности точки
– любая точка окрестности точки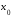 ,
функции
,
функции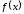 и
и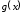 непрерывны, дифференцируемы и
непрерывны, дифференцируемы и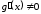
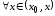 .Поэтому применима
теорема Коши:
.Поэтому применима
теорема Коши:
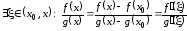 .
.
Если
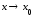 ,
то
,
то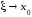 и поэтому
и поэтому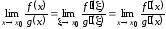 .
.
Случай
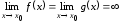 оставляем без доказательства.
оставляем без доказательства.
Замечания.
1. При применении правила Лопиталя дифференцируется числитель и знаменатель дроби отдельно.
2. Правило Лопиталя применяется только к дробям.
Чтобы
применить правило Лопиталя для
неопределенностей вида
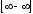 ,
, ,
,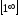 ,
,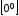 и т. д., нужно предварительно исследуемое
выражение преобразовать к дроби.
Рассмотрим примеры раскрытия некоторых
неопределенностей.
и т. д., нужно предварительно исследуемое
выражение преобразовать к дроби.
Рассмотрим примеры раскрытия некоторых
неопределенностей.
Неопределенность
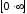 :
:
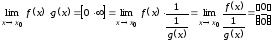 .
.
Неопределенность
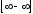 :
:

Неопределенности
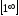 ,
,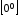 ,
,
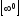 :
:
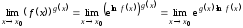 .
.
Пример
4.5. Вычислить
предел
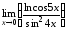 .
.
Решение.
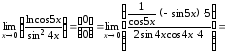
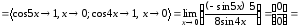
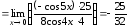 .
.
Пример
4.6. Вычислить
предел
 .
.
Решение.
 .
.
Пример
4.7.
Вычислить предел
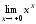 .
.
Решение.
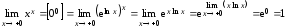 .
.
Пример
4.8. Вычислить
предел
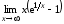 .
.
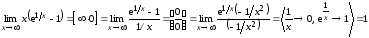 .
.
Пример
4.9.
Вычислить предел
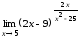 .
.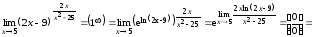
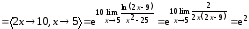 .
.
3. Иногда правило Лопиталя применяется несколько раз, если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы должны оставаться справедливыми.
Пример
4.10. Вычислить
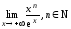 .
.
Решение.
Значение
предела
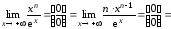
 позволяет
сравнить бесконечно большие при
позволяет
сравнить бесконечно большие при
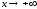 функции: показательная функция
функции: показательная функция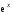 – бесконечно большая функция большего
порядка по сравнению со степенной
функцией
– бесконечно большая функция большего
порядка по сравнению со степенной
функцией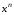 – бесконечно большой при
– бесконечно большой при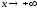 .
.
4.
Правило
Лопиталя не
является универсальным,
оно применимо лишь тогда, когда существует
предел
отношения производных
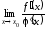 .
.
Пример
4.11. Значение
предела
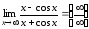 получить по правилу Лопиталянельзя,
поскольку
получить по правилу Лопиталянельзя,
поскольку
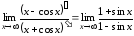 – не существует (
– не существует ( не существует, см. решение примера 3.6).
Однако исходный пределсуществует,
его легко можно вычислить другим
способом, например, так:
не существует, см. решение примера 3.6).
Однако исходный пределсуществует,
его легко можно вычислить другим
способом, например, так:
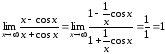 ,
применяя теорему о пределе произведения
бесконечно малой функции на ограниченную,
в нашем случае,
,
применяя теорему о пределе произведения
бесконечно малой функции на ограниченную,
в нашем случае,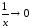 при
при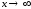 ,
,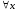 имеет место неравенство
имеет место неравенство .
.
4.6. Формула Тейлора для многочленов
В 1715 году Брук Тейлор9опубликовал формулу для разложения функции в степенной ряд, которая явилась мощным инструментом для исследования функций и приближенных вычислений.
Рассмотрим
вспомогательную
задачу. Пусть функция
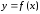 имеет в окрестности точки
имеет в окрестности точки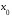 производные
до
производные
до
 -
го порядка включительно. Требуется
найти многочлен
-
го порядка включительно. Требуется
найти многочлен
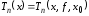
степени
не выше
 такой, что для всех
такой, что для всех выполняются равенства
выполняются равенства
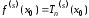 . (4.15)
. (4.15)
Будем
искать
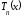 в виде многочлена по степеням разности
в виде многочлена по степеням разности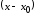 :
:
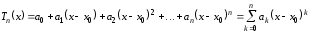 , (4.16)
, (4.16)
где
коэффициенты
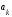 нужно
определить.
нужно
определить.
Найдем
производные многочлена
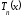 порядка
порядка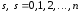 :
:
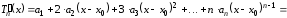
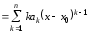 ,
,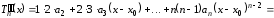 (4.17)
(4.17)
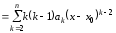 ,
,
и далее,
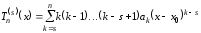 .
.
Из
(4.16) и (4.17) при
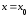 получаем
получаем
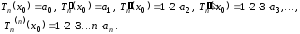
Отсюда
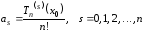 .
.
Значит, с учетом (4.15), должны выполняться равенства
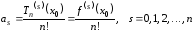 .
.
Таким образом, поставленную задачу решает многочлен
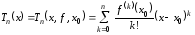 . (4.18)
. (4.18)
Многочлен
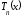 ,
заданный формулой (4.18), называютмногочленом
Тейлора порядка
,
заданный формулой (4.18), называютмногочленом
Тейлора порядка
 функции
функции
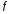 в точке
в точке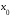 .
Он единственен.
.
Он единственен.
