
- •Глава 3. Производная функции одной переменной
- •3.1. Производная функции в точке
- •X Физический смысл производной
- •Геометрический смысл производной. Связь с существованием касательной
- •Уравнения касательной и нормали
- •Бесконечные производные
- •Односторонние производные
- •3.2. Дифференцируемость функции одной переменной Определение функции, дифференцируемой в точке
- •Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
- •Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
- •3.3. Правила вычисления производных
- •3.6. Производные некоторых элементарных функций (таблица производных)
- •3.7. Логарифмическая производная
- •3.8. Производная функции, заданной параметрически
- •3.9. Дифференцирование функций, заданных неявно
- •Глава 4. Производные и дифференциалы высших порядков
- •4.1. Дифференциал функции одной переменной
- •Геометрический смысл дифференциала
- •Инвариантность формы дифференциала первого порядка
- •Дифференциал и приближенные вычисления
- •4.2. Производные и дифференциалы высших порядков Понятие производной - го порядка
- •Дифференциалы высших порядков
- •Правила вычисления производной суммы - го порядка. Формула Лейбница для- й производной произведения двух функций
- •4.3. Теоремы о непрерывных и дифференцируемых функциях
- •4.4. Формулы конечных приращений, их приложения
- •Теорема Ролля5о среднем
- •4.5. Раскрытие неопределенностей (Правило Лопиталя)
- •4.6. Формула Тейлора для многочленов
- •4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано10
- •4.8. Формула Тейлора с остаточным членом в форме Лагранжа
- •Формула Маклорена11
- •4.9. Разложения основных элементарных функций (асимптотические формулы)
- •Глава 5. Исследование и построение графиков функции одной переменной
- •5.1. Условия возрастания и убывания функции
- •5.2. Локальный экстремум Теорема 5.2 (первое достаточное условие локального экстремума дифференцируемой функции)
- •5.3. Абсолютный экстремум функции
- •5.4. Выпуклость и точки перегиба графика функции
- •Точки перегиба графика функции
- •5.5. Асимптоты графика функции
- •5.6. Схема исследования функций и построения кривых
3.2. Дифференцируемость функции одной переменной Определение функции, дифференцируемой в точке
Функция
 ,
определенная на множестве
,
определенная на множестве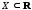 ,
называетсядифференцируемой
в
точке
,
называетсядифференцируемой
в
точке
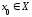 ,
предельной для множества
,
предельной для множества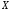 ,
если существует такаялинейная
относительно приращения
,
если существует такаялинейная
относительно приращения
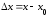 функция
функция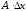 (
(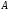 –
некоторое число), что приращение
–
некоторое число), что приращение
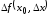 функции
функции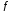 представимо в виде
представимо в виде
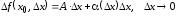 (3.2)
(3.2)
где
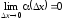 .
Так как
.
Так как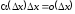 ,
то (3.2) можно записать в виде
,
то (3.2) можно записать в виде
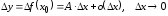 .
.
Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
Для
того чтобы функция
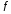 была дифференцируемой в точке
была дифференцируемой в точке ,необходимо
и
достаточно,
чтобы она имела в этой точке конечную
производную.
,необходимо
и
достаточно,
чтобы она имела в этой точке конечную
производную.
Доказательство.
Необходимость.
Пусть функция
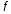 дифференцируема в точке
дифференцируема в точке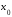 .
Тогда ее приращение можно представить
в виде (3.2). Имеем
.
Тогда ее приращение можно представить
в виде (3.2). Имеем
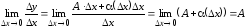 .
.
Следовательно,
производная
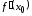 существует и
существует и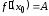 .
.
Достаточность.
Пусть
существует конечная производная
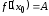 .
Тогда по определению производной
.
Тогда по определению производной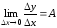 .
Положим
.
Положим
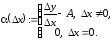 (3.3)
(3.3)
Функция
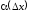 является бесконечно малой при
является бесконечно малой при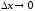 и непрерывной при
и непрерывной при
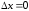 .
Действительно,
.
Действительно,
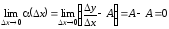 .
Кроме того, из (3.3) вытекает
.
Кроме того, из (3.3) вытекает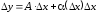 .
Тем самым доказано, что функция
.
Тем самым доказано, что функция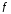 дифференцируема в точке
дифференцируема в точке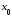 .
.
Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
Если
функция
 дифференцируема в точке
дифференцируема в точке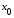 ,
то она непрерывна в этой точке.
,
то она непрерывна в этой точке.
Доказательство.
Из
(3.2) вытекает равенство
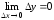 ,
то есть функция
,
то есть функция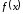 непрерывна в точке
непрерывна в точке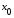 .
.
Обратное утверждение неверно. Непрерывность функции в точке является необходимым условием существования производной функции в этой точке, но не является достаточным.
В
самом деле, пусть
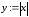 .
Функция
.
Функция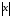 не имеет производной в нуле (пример
3.4), хотя она и непрерывна в любой точке
не имеет производной в нуле (пример
3.4), хотя она и непрерывна в любой точке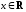 .
.
Связь понятий: непрерывность функции, дифференцируемость функции, существование производной можно представить следующей схемой:
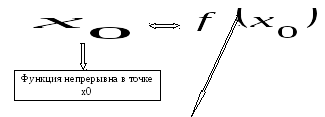
3.3. Правила вычисления производных
Теорема
3.5. Пусть
функции
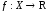 и
и
 имеют в точке
имеют в точке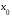 ,
предельной для
,
предельной для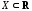 ,
конечные производные
,
конечные производные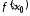 и
и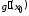 .
Тогда в этой точке существуют производные
.
Тогда в этой точке существуют производные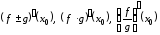 ,
если
,
если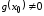 ,
и выполняются равенства:
,
и выполняются равенства:
1.
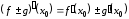 .
.
2.
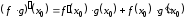 .
.
3.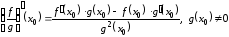 .
.
Доказательство.
1.
Имеем

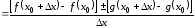 .
Так
как существуют производные
.
Так
как существуют производные
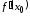 и
и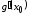 ,
то переходя к пределу при
,
то переходя к пределу при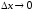 ,
получим
,
получим
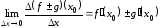 .
.
2.
Имеем
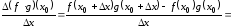
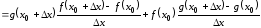 .
.
Так
как
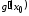 существует, то функция
существует, то функция
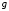 непрерывна в точке
непрерывна в точке
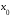 .
Поэтому
.
Поэтому
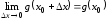 .
Значит,
.
Значит,
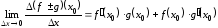 .
.
Следствие.
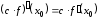 ,
,
если
 – постоянная величина.
– постоянная величина.
3.
Сначала рассмотрим случай, когда
 ,
т. е. получим формулу для производной
дроби
,
т. е. получим формулу для производной
дроби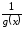 .
Имеем
.
Имеем
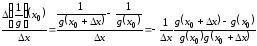 . (3.4)
. (3.4)
Так
как функция
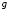 непрерывна в точке
непрерывна в точке
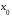 и
и
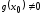 ,
то существует такая окрестность
,
то существует такая окрестность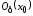 ,
что для любого
,
что для любого
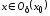 функция
функция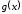 сохраняет знак, т. е.
сохраняет знак, т. е.
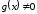 .
Выражение в правой части(3.4)
имеет предел при
.
Выражение в правой части(3.4)
имеет предел при
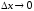 ,
поэтому существует
,
поэтому существует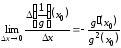 ,
т. е.
,
т. е.
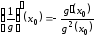 .
.
Теперь
с помощью формулы для производной
произведения получим
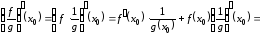

 ,
т. е.
,
т. е.
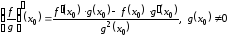 .
.
3.4. Дифференцирование сложной функции
Теорема 3.6 (о дифференцировании сложной функции)
Если
функция
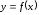 дифференцируема в точке
дифференцируема в точке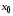 ,
а функция
,
а функция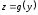 дифференцируема в точке
дифференцируема в точке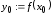 ,
то функция
,
то функция дифференцируема в точке
дифференцируема в точке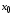 и имеет место равенство
и имеет место равенство
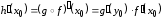 . (3.5)
. (3.5)
Доказательство.
Дадим
приращение
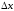 переменной
переменной
 и обозначим соответствующее приращение
функции
и обозначим соответствующее приращение
функции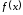 через
через
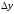 .
Тогда
.
Тогда
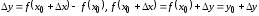 .
Заметим также, что из дифференцируемости
.
Заметим также, что из дифференцируемости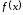 в точке
в точке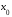 следует ее
непрерывность в этой точке:
следует ее
непрерывность в этой точке:
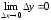 .
Учитывая эти замечания, находим
производную:
.
Учитывая эти замечания, находим
производную:
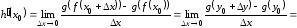
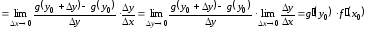 .
.
Итак, мы получили формулу
 .
.
Замечание.
Так как
производная
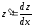 ,
то для производной сложной функции
верна формула
,
то для производной сложной функции
верна формула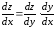 .
.
3.5 Дифференцирование обратной функции
Теорема 3.7 (о производной обратной функции)
Пусть
функция
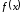 строго
монотонна и непрерывна в окрестности
точки
строго
монотонна и непрерывна в окрестности
точки
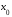 .
Если существует
.
Если существует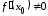 ,
то обратная функция
,
то обратная функция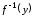 существует в некоторой окрестности
точки
существует в некоторой окрестности
точки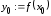 и имеет в
этой точке производную, и справедливо
равенство
и имеет в
этой точке производную, и справедливо
равенство
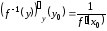 ,
,
т. е.
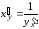 .
.
Доказательство.
В
силу непрерывности функции
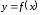 в точке
в точке
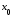 из
из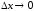 следует
следует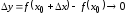 .
Так как обратная функция
.
Так как обратная функция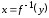 в силу монотонности функции
в силу монотонности функции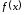 существует и непрерывна в точке
существует и непрерывна в точке
 ,
то из того, что
,
то из того, что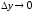 ,
вытекает
,
вытекает
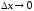 .
Таким образом, в нашем случае, условия
.
Таким образом, в нашем случае, условия и
и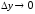 равносильны.
равносильны.
Так
как функция
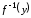 строго монотонна, то из неравенства
строго монотонна, то из неравенства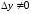 следует неравенство
следует неравенство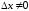 .
Поэтому
.
Поэтому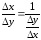 .
Если
.
Если
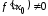 ,
то, пользуясь равносильностью условий
,
то, пользуясь равносильностью условий
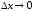 и
и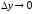 ,
находим
,
находим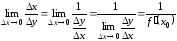 .
Таким образом,
.
Таким образом,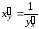 .
.
