
- •Глава 3. Производная функции одной переменной
- •3.1. Производная функции в точке
- •X Физический смысл производной
- •Геометрический смысл производной. Связь с существованием касательной
- •Уравнения касательной и нормали
- •Бесконечные производные
- •Односторонние производные
- •3.2. Дифференцируемость функции одной переменной Определение функции, дифференцируемой в точке
- •Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
- •Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
- •3.3. Правила вычисления производных
- •3.6. Производные некоторых элементарных функций (таблица производных)
- •3.7. Логарифмическая производная
- •3.8. Производная функции, заданной параметрически
- •3.9. Дифференцирование функций, заданных неявно
- •Глава 4. Производные и дифференциалы высших порядков
- •4.1. Дифференциал функции одной переменной
- •Геометрический смысл дифференциала
- •Инвариантность формы дифференциала первого порядка
- •Дифференциал и приближенные вычисления
- •4.2. Производные и дифференциалы высших порядков Понятие производной - го порядка
- •Дифференциалы высших порядков
- •Правила вычисления производной суммы - го порядка. Формула Лейбница для- й производной произведения двух функций
- •4.3. Теоремы о непрерывных и дифференцируемых функциях
- •4.4. Формулы конечных приращений, их приложения
- •Теорема Ролля5о среднем
- •4.5. Раскрытие неопределенностей (Правило Лопиталя)
- •4.6. Формула Тейлора для многочленов
- •4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано10
- •4.8. Формула Тейлора с остаточным членом в форме Лагранжа
- •Формула Маклорена11
- •4.9. Разложения основных элементарных функций (асимптотические формулы)
- •Глава 5. Исследование и построение графиков функции одной переменной
- •5.1. Условия возрастания и убывания функции
- •5.2. Локальный экстремум Теорема 5.2 (первое достаточное условие локального экстремума дифференцируемой функции)
- •5.3. Абсолютный экстремум функции
- •5.4. Выпуклость и точки перегиба графика функции
- •Точки перегиба графика функции
- •5.5. Асимптоты графика функции
- •5.6. Схема исследования функций и построения кривых
Инвариантность формы дифференциала первого порядка
Пусть
функция
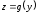 дифференцируема в точке
дифференцируема в точке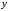 .
Тогда
.
Тогда
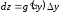 (4.2)
(4.2)
Рассмотрим два случая:
если
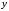 – независимая переменная, то
– независимая переменная, то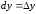 ,
поэтому
,
поэтому
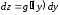 ;
;
если
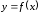 дифференцируема в точке
дифференцируема в точке ,
то сложная функция
,
то сложная функция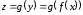 дифференцируема в точке
дифференцируема в точке и
и
 . (4.3)
. (4.3)
Таким образом, дифференциал функции равен произведению производной по некоторой переменной на дифференциал этой переменной.
Свойство первого дифференциала иметь одинаковые выражения через дифференциалы независимой переменной (в случае 1)) и зависимой переменной (в случае 2)) называют инвариантностью формы первого дифференциала.
Замечание.
В (4.2)
 ,
здесь
,
здесь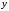 – независимая переменная. В (4.3)
– независимая переменная. В (4.3)
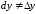 ,
здесь
,
здесь
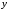 – зависимая переменная,
– зависимая переменная,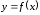 .
.
Так,
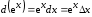 ,
,
 .
.
Дифференциал и приближенные вычисления
Если
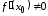 ,
то
,
то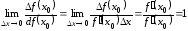 ,
то есть
,
то есть
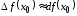 ,
,
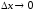 . (4.4)
. (4.4)
Этим
равенством часто пользуются для
приближенного вычисления значений
дифференцируемой функции из некоторой
 -
окрестности точки
-
окрестности точки
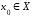 при достаточно малом
при достаточно малом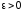 .
Формулу (4.4) записывают в виде
.
Формулу (4.4) записывают в виде
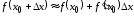 ,
,
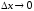 . (4.5)
. (4.5)
Так
как
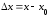 ,
то
,
то и формула (4.5) принимает вид
и формула (4.5) принимает вид
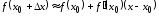 ,
,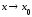 . (4.6)
. (4.6)
Графиком
функции правой части (4.6) является прямая
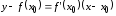 ,
проходящая через точку
,
проходящая через точку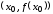 и имеющая угловой коэффициент
и имеющая угловой коэффициент .
Эта прямая – касательная к графику
функции в точке
.
Эта прямая – касательная к графику
функции в точке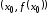 – доставляет линейное приближение
функцииf
в окрестности точки
– доставляет линейное приближение
функцииf
в окрестности точки
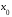 .
Следовательно,
геометрически (4.6) означает, что в
окрестности точки
.
Следовательно,
геометрически (4.6) означает, что в
окрестности точки
 график функции
график функции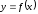 сливается с отрезком касательной, т. е.
«спрямляется». Говорят, что соотношением
(4.4) функция
сливается с отрезком касательной, т. е.
«спрямляется». Говорят, что соотношением
(4.4) функция линеаризована
в окрестности точки
линеаризована
в окрестности точки
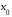 .
.
Если
аргумент х
вычислен с относительной погрешностью
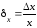 ,
то значение функции
,
то значение функции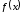 – с относительной погрешностью
– с относительной погрешностью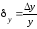 ,
определяется по формуле
,
определяется по формуле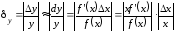 или
или
 , (4.7)
, (4.7)
где
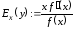 – эластичность
функции
– эластичность
функции
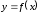 в точке х
(подробнее
см. п. ).
в точке х
(подробнее
см. п. ).
Пример
4.1. Найти
время удвоения вклада в банк, если ставка
банковского процента за год составляет
10 % годовых.
Найдем
количество лет Т, в течение которых
сумма вклада увеличится в 2 раза. За год
вклад увеличивается в
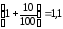 раз, поэтому заТ
лет вклад увеличится в
раз, поэтому заТ
лет вклад увеличится в
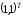 раз. Т. о., необходимо решить уравнение
раз. Т. о., необходимо решить уравнение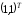 =2.
Логарифмируя, получаем
=2.
Логарифмируя, получаем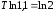 ,
откуда
,
откуда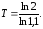 Для приближенного вычисления
Для приближенного вычисления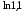 используем понятие дифференциала.
Полагая
используем понятие дифференциала.
Полагая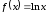 ,
найдем
,
найдем и в соответствии с (4.5)
и в соответствии с (4.5)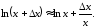 В данном примере прих
=1 и
В данном примере прих
=1 и
 получим
получим Так как
Так как ,
то время удвоения вклада
,
то время удвоения вклада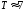 (лет).
(лет).
Пример 4.2. С какой относительной погрешностью надо измерить радиус шара, чтобы объем его можно было определить с точностью до 1%?
Решение.
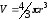 .
Значит,
.
Значит, .
Нужно, чтобы
.
Нужно, чтобы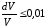 ,
значит,
,
значит,
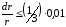 .
Ответ:
с точностью 1/3%.
.
Ответ:
с точностью 1/3%.
Пример
4.3. На сколько
процентов увеличится
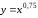 ,
еслих
увеличится на 2%.
,
еслих
увеличится на 2%.
Решение.
Найдем эластичность функции
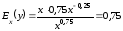 и по формуле (4.7) относительная погрешность
и по формуле (4.7) относительная погрешность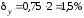 .
.
Упражнения.
1. Вычислить приближенно: а)
 ;
б)
;
б)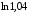 ;
в)
;
в)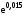 ;
г)
;
г) .
.
2. На сколько процентов увеличится площадь круга, если его радиус увеличится на 1%?
3.
Известно, что
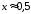 и
и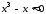 .
С какой точностью выполняется приближенное
равенство
.
С какой точностью выполняется приближенное
равенство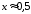 ,
если
,
если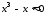 выполняется с точностью 0,001.
выполняется с точностью 0,001.
4.
На сколько процентов изменится величина
степени
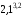 при изменении основания степени на 3%?
при изменении основания степени на 3%?
4.2. Производные и дифференциалы высших порядков Понятие производной - го порядка
Пусть
для функции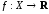 множество
множество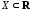 не имеет изолированных точек и пусть
для любого
не имеет изолированных точек и пусть
для любого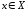 существует производная
существует производная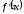 .
Функция
.
Функция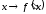 называетсяпервой
производной
функции
называетсяпервой
производной
функции
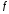 и обозначается
и обозначается
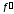 .
Индукцией определим производную функции
.
Индукцией определим производную функции
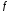 произвольного порядка. Если функция
произвольного порядка. Если функция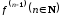 дифференцируема на множестве
дифференцируема на множестве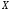 ,
то ее производная
,
то ее производная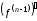 называется
называется
 - й производной
функции
- й производной
функции
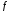 на множестве
на множестве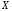 и обозначается
через
и обозначается
через
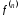 .
Таким образом,
.
Таким образом,
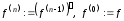 .
.
При
этом функция
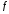 называется
называется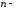 дифференцируемой
(
дифференцируемой
( раз
дифференцируемой)
на
раз
дифференцируемой)
на
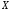 .
.
