
- •Глава 3. Производная функции одной переменной
- •3.1. Производная функции в точке
- •X Физический смысл производной
- •Геометрический смысл производной. Связь с существованием касательной
- •Уравнения касательной и нормали
- •Бесконечные производные
- •Односторонние производные
- •3.2. Дифференцируемость функции одной переменной Определение функции, дифференцируемой в точке
- •Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
- •Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
- •3.3. Правила вычисления производных
- •3.6. Производные некоторых элементарных функций (таблица производных)
- •3.7. Логарифмическая производная
- •3.8. Производная функции, заданной параметрически
- •3.9. Дифференцирование функций, заданных неявно
- •Глава 4. Производные и дифференциалы высших порядков
- •4.1. Дифференциал функции одной переменной
- •Геометрический смысл дифференциала
- •Инвариантность формы дифференциала первого порядка
- •Дифференциал и приближенные вычисления
- •4.2. Производные и дифференциалы высших порядков Понятие производной - го порядка
- •Дифференциалы высших порядков
- •Правила вычисления производной суммы - го порядка. Формула Лейбница для- й производной произведения двух функций
- •4.3. Теоремы о непрерывных и дифференцируемых функциях
- •4.4. Формулы конечных приращений, их приложения
- •Теорема Ролля5о среднем
- •4.5. Раскрытие неопределенностей (Правило Лопиталя)
- •4.6. Формула Тейлора для многочленов
- •4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано10
- •4.8. Формула Тейлора с остаточным членом в форме Лагранжа
- •Формула Маклорена11
- •4.9. Разложения основных элементарных функций (асимптотические формулы)
- •Глава 5. Исследование и построение графиков функции одной переменной
- •5.1. Условия возрастания и убывания функции
- •5.2. Локальный экстремум Теорема 5.2 (первое достаточное условие локального экстремума дифференцируемой функции)
- •5.3. Абсолютный экстремум функции
- •5.4. Выпуклость и точки перегиба графика функции
- •Точки перегиба графика функции
- •5.5. Асимптоты графика функции
- •5.6. Схема исследования функций и построения кривых
5.5. Асимптоты графика функции
Определение.
Пусть для функции
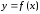 существует такая прямая, что расстояние
от точки
существует такая прямая, что расстояние
от точки графика функции до этой прямой стремится
к нулю при бесконечном удалении точки
графика функции до этой прямой стремится
к нулю при бесконечном удалении точки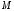 от начала координат. Тогда такая прямая
называетсяасимптотой
графика
функции.
от начала координат. Тогда такая прямая
называетсяасимптотой
графика
функции.
Из определения видно, что если график функции имеет асимптоту, то «вдали» от начала координат он похож на прямую линию.
В
случае вертикальной асимптоты (рис.
5.10) неограниченное удаление точки
графика от начала координат равносильно
тому, что
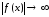 при
при ,
а стремление к нулю расстояния между
графиком и асимптотой равносильно тому,
что
,
а стремление к нулю расстояния между
графиком и асимптотой равносильно тому,
что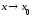 .
Отсюда следует
.
Отсюда следует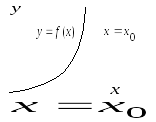
Теорема
5.7. Прямая
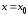 являетсявертикальной
асимптотой
графика функции
являетсявертикальной
асимптотой
графика функции
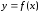 тогда и
только тогда, когда хотя бы одно из
предельных значений
тогда и
только тогда, когда хотя бы одно из
предельных значений
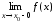 или
или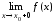 равно +
равно +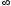 или –.
или –.
Замечание. Непрерывные функции вертикальных асимптот не имеют.
Можно заметить, что вертикальные асимптоты тесно связаны с точками разрыва второго рода.
Пример
5.7. Найти
вертикальные асимптоты графика функции
 .
Находим
.
Находим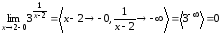 ,
,
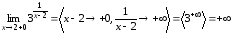 .
Здесь прямая
.
Здесь прямая
 – правая вертикальная асимптота.
Заметим, что
– правая вертикальная асимптота.
Заметим, что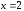 – точка разрыва второго рода.
– точка разрыва второго рода.
Пример
5.8.
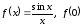 не существует. Имеем
не существует. Имеем .
Вертикальных асимптот график функции
не имеет.
.
Вертикальных асимптот график функции
не имеет.
Пример
5.9. Функция
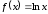 не имеет разрывов, однако
не имеет разрывов, однако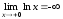 .
Поэтому
.
Поэтому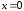 – вертикальная асимптота.
– вертикальная асимптота.
Перейдем к вопросу о нахождении наклонных асимптот.
Теорема
5.8. Для
существования наклонной
асимптоты
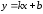 графика функции
графика функции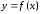 при
при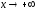 (
(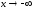 )
необходимо
и достаточно, чтобы существовали конечные
пределы:
)
необходимо
и достаточно, чтобы существовали конечные
пределы:
 (5.2)
(5.2)
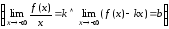 .
(5.3)
.
(5.3)
При
этом при
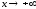 и при
и при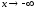 указанные пределы могут быть различными
(правая
наклонная
асимптота
и, соответственно, левая
наклонная
асимптота).
указанные пределы могут быть различными
(правая
наклонная
асимптота
и, соответственно, левая
наклонная
асимптота).
Доказательство.
Пусть
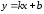 – наклонная
асимптота графика функции. Расстояние
от точки графика функции до асимптоты
изображается на рисунке (рис. 5.11) отрезком
КМ.
Заметим, что
– наклонная
асимптота графика функции. Расстояние
от точки графика функции до асимптоты
изображается на рисунке (рис. 5.11) отрезком
КМ.
Заметим, что
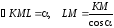 .
Так как координаты точки
.
Так как координаты точки есть
есть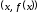 ,
то координаты точки
,
то координаты точки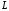 есть
есть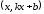 .
Поэтому
.
Поэтому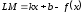 .
.
По
определению
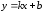 – наклонная
асимптота
– наклонная
асимптота
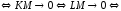
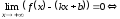
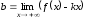 .Тогда существует
бесконечно малая функция
.Тогда существует
бесконечно малая функция
 при
при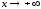 такая, что
такая, что
 .
Разделим обе части последнего равенства
на
.
Разделим обе части последнего равенства
на
 и в полученном равенстве перейдем к
пределу при
и в полученном равенстве перейдем к
пределу при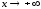 :
: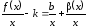 ,
,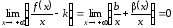 .
Отсюда
.
Отсюда .
Теорема доказана.
.
Теорема доказана.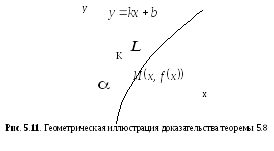
Замечание.
В случае
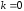 наклонная асимптота становитсягоризонтальной.
наклонная асимптота становитсягоризонтальной.
Замечание.
Если хотя
бы один из пределов (5.2) при
 ((5.3) при
((5.3) при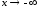 )
не существует или является бесконечным,
то график функции наклонных асимптот
не имеет.
)
не существует или является бесконечным,
то график функции наклонных асимптот
не имеет.
Пример
5.10. Найти
асимптоты графика функции
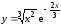 .
.
Область
определения функции
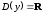 ;
;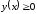 при
при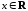 ,
,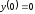 .
.
Вертикальных
асимптот нет, т. к. функция непрерывна
при всех
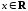 .
Найдем наклонные асимптоты
.
Найдем наклонные асимптоты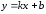 :
:
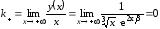 ;
;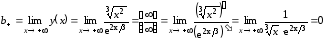 ;
;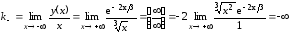 .
.
Следовательно,
при
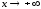 имеем правую горизонтальную асимптоту
имеем правую горизонтальную асимптоту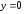 ;
при
;
при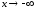 наклонных и горизонтальных асимптот
нет.
наклонных и горизонтальных асимптот
нет.
5.6. Схема исследования функций и построения кривых
Найти область определения функции
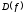 .
.Отметить особенности функции (периодичность, четность и нечетность, сохранение знака), найти точки пересечения графика функции с осями координат.
Если граничные точки области определения функции принадлежат ей, то найти значение функции в этих точках, в противном случае – выяснить поведение функции в окрестности этих точек. Найти вертикальные асимптоты, если они существуют.
Исследовать поведение функции при
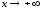 и при
и при
 ,
найти горизонтальные или наклонные
асимптоты или убедиться в их отсутствии.
,
найти горизонтальные или наклонные
асимптоты или убедиться в их отсутствии.Найти интервалы монотонности функции и точки экстремума.
Указать интервалы сохранения направления выпуклости и точки перегиба графика функции.
По результатам исследования функции строится ее график.
Пример 5.11. Исследовать функции и построить их графики:
|
|
|
|
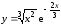 .
.
Область определения функции
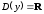 ;
;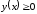 при
при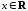 ,
,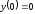 .
.Вертикальных асимптот нет, т. к. функция непрерывна при всех
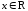 .
Найдем наклонные асимптоты
.
Найдем наклонные асимптоты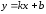 :
:
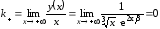 ;
;
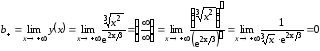 ;
;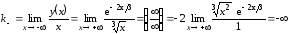 .
Следовательно,
при
.
Следовательно,
при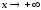 имеем правую горизонтальную асимптоту
имеем правую горизонтальную асимптоту
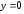 ;
при
;
при
 наклонных и горизонтальных асимптот
нет.
наклонных и горизонтальных асимптот
нет.
Определим промежутки монотонности и локальные экстремумы данной функции. Первая производная функции
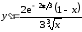 .
Находим критические точки:
.
Находим критические точки: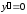 при
при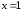 и
и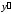 не существует при
не существует при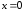 .
При
.
При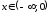 и при
и при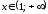
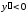 ,
при
,
при
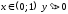 .
На каждом из промежутков
.
На каждом из промежутков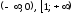 функция убывает, на промежутке
функция убывает, на промежутке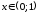 функция возрастает (рис. 5.12).
функция возрастает (рис. 5.12).

Точка
локального минимума
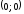 ;
локального максимума
;
локального максимума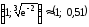 ;
в точке
;
в точке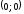 – вертикальная полукасательная
– вертикальная полукасательная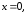
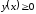 .
.
Определим промежутки выпуклости и точки перегиба графика функции. Вторая производная равна
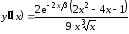 .
Найдем корни уравнения
.
Найдем корни уравнения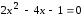 :
: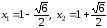
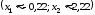 .
Так как
.
Так как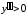 при
при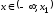 и при
и при
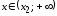 ,
то на этих интервалах график функции
является выпуклым вниз. Аналогично
при
,
то на этих интервалах график функции
является выпуклым вниз. Аналогично
при
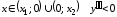 ,
т. е. на соответствующих интервалах
график функции выпуклый вверх, рис.
5.13.
,
т. е. на соответствующих интервалах
график функции выпуклый вверх, рис.
5.13.
Точки
перегиба графика функции
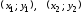 .
Здесь
.
Здесь
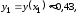
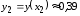 .
График функции представлен на рис. 5.14.
.
График функции представлен на рис. 5.14.

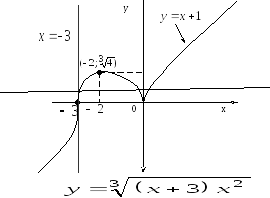
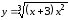 .
.
Область
определения
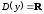 ;
;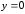 при
при и при
и при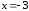 .
При
.
При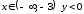 ,
а при
,
а при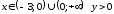 .
Точки
.
Точки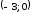 и
и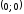 являются точками пересечения графика
функции с осями координат.
являются точками пересечения графика
функции с осями координат.
Вертикальных асимптот нет, так как функция определена и непрерывна на множестве действительных чисел. Для наклонной асимптоты
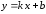 найдем коэффициенты:
найдем коэффициенты:
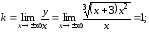

т.
е.
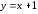 – наклонная асимптота.
– наклонная асимптота.
Найдем производную
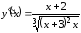 ;
;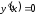 при
при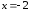 и
и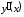 не существует при
не существует при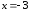 и при
и при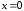 .
.
При
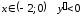 ;
при
;
при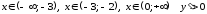 .
На промежутке
.
На промежутке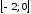 функция убывает, на промежутках
функция убывает, на промежутках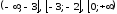 возрастает (рис. 5.15). В точке (2;
возрастает (рис. 5.15). В точке (2;
 )
функция имеет локальный максимум, в
точке
)
функция имеет локальный максимум, в
точке локальный минимум. Отметим, что
локальный минимум. Отметим, что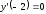 ,
т. е. график функции имеет в этой точке
горизонтальную касательную. В точке
(3;
0) имеем вертикальную касательную
,
т. е. график функции имеет в этой точке
горизонтальную касательную. В точке
(3;
0) имеем вертикальную касательную
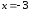 (функция
(функция в точке
в точке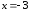 непрерывна и
непрерывна и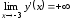 ).
Поскольку
).
Поскольку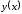 непрерывна в нуле и
непрерывна в нуле и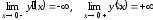 ;
то полупрямая
;
то полупрямая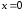 ,
,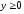 является и левой и правой полукасательной
к графику функции в точке
является и левой и правой полукасательной
к графику функции в точке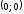 .
.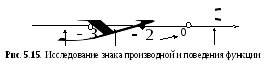
Определим
промежутки выпуклости и точки перегиба
графика функции. Находим вторую
производную
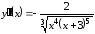 .
Знаки второй производной:
.
Знаки второй производной: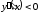 при
при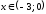 и при
и при
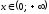 ,
,
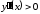 при
при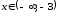 (рис. 5.16). Точка перегиба графика функции
(рис. 5.16). Точка перегиба графика функции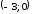 .
На промежутке
.
На промежутке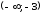 график функции выпуклый вниз; на
промежутках
график функции выпуклый вниз; на
промежутках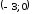 и (0; +)
– выпуклый вверх.
и (0; +)
– выпуклый вверх.
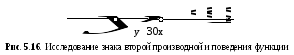
График функции представлен на рис. 5.17.
1Жозеф Луи Лагранж (1736–1813) – знаменитый французский математик и механик, член Парижской АН. Ему принадлежат выдающиеся исследования по различным вопросам математического анализа, теории чисел, алгебре, дифференциальным уравнениям, астрологии и др.
2Исаак Ньютон (1642–1727) – английский физик, механик, астроном и математик. Разработал (наряду с Лейбницем) основы дифференциального и интегрального исчисления.
3Готфрид Вильгельм Лейбниц (1646–1716) – немецкий философ-идеалист, физик, математик, изобретатель, историк. В математике важнейшей заслугой Лейбница (наряду с И.Ньютоном и независимо от него) является разработка дифференциального и интегрального исчисления. Лейбниц изобрел первый интегрирующий механизм и уникальную для того времени счетную машину.
4Пьер Ферма (1601–1665 гг.) – выдающийся французский математик, по профессии юрист. Ферма является одним из создателей теории чисел. Сформулированная им теорема о том, что уравнение не разрешимо в целых числах, была доказана только в 1994 г. Эндрю Уайлсом.
5Мишель Ролль (1652 –1719 гг.) – французский математик. Его исследования были не замечены и забыты современниками, и по достоинству оценены намного позже.
6Коши Огюстен Луи (1789–1857) – французский математик, один из наиболее активных творцов современного языка и аппарата классического анализа.
7Иоганн Бернулли (1667–1748) – швейцарский математик, младший брат Якоба Бернулли. Сотрудничал с Лейбницем в разработке дифференциального и интегрального исчислений. Продвинул теорию дифференциальных уравнений, исследования в области механики и др.
8Лопиталь Гийом Франсуа Антуан (1661–1704) – французский математик, автор первого учебника по дифференциальному исчислению (1696), в основу которого легли лекции швейцарского математика Иоганна Бернулли.
9 Брук Тейлор (1685 –1731) – английский математик. Ему принадлежат заслуги в разработке теории конечных разностей, автор работ о полете снарядов, взаимодействии магнитов, капиллярности и др.
10 Джузеппе Пеано (1858 – 1932) – итальянский математик. Занимался формально логическим обоснованием математики. Известен его пример непрерывной (жордановой) кривой, целиком заполняющей некоторый квадрат.
11Колин Маклорен (1698–1746) – шотландский математик. Математические исследования относятся к анализу (теория рядов, конечные разности), ряд работ к механике.

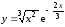 ;
;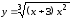 .
.