
- •Глава 3. Производная функции одной переменной
- •3.1. Производная функции в точке
- •X Физический смысл производной
- •Геометрический смысл производной. Связь с существованием касательной
- •Уравнения касательной и нормали
- •Бесконечные производные
- •Односторонние производные
- •3.2. Дифференцируемость функции одной переменной Определение функции, дифференцируемой в точке
- •Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
- •Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
- •3.3. Правила вычисления производных
- •3.6. Производные некоторых элементарных функций (таблица производных)
- •3.7. Логарифмическая производная
- •3.8. Производная функции, заданной параметрически
- •3.9. Дифференцирование функций, заданных неявно
- •Глава 4. Производные и дифференциалы высших порядков
- •4.1. Дифференциал функции одной переменной
- •Геометрический смысл дифференциала
- •Инвариантность формы дифференциала первого порядка
- •Дифференциал и приближенные вычисления
- •4.2. Производные и дифференциалы высших порядков Понятие производной - го порядка
- •Дифференциалы высших порядков
- •Правила вычисления производной суммы - го порядка. Формула Лейбница для- й производной произведения двух функций
- •4.3. Теоремы о непрерывных и дифференцируемых функциях
- •4.4. Формулы конечных приращений, их приложения
- •Теорема Ролля5о среднем
- •4.5. Раскрытие неопределенностей (Правило Лопиталя)
- •4.6. Формула Тейлора для многочленов
- •4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано10
- •4.8. Формула Тейлора с остаточным членом в форме Лагранжа
- •Формула Маклорена11
- •4.9. Разложения основных элементарных функций (асимптотические формулы)
- •Глава 5. Исследование и построение графиков функции одной переменной
- •5.1. Условия возрастания и убывания функции
- •5.2. Локальный экстремум Теорема 5.2 (первое достаточное условие локального экстремума дифференцируемой функции)
- •5.3. Абсолютный экстремум функции
- •5.4. Выпуклость и точки перегиба графика функции
- •Точки перегиба графика функции
- •5.5. Асимптоты графика функции
- •5.6. Схема исследования функций и построения кривых
4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано10
Покажем,
что именно многочлен Тейлора
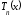 функции
функции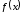 задаетнаилучшее
локальное приближение
этой функции. Для этого оценим погрешность
приближения
задаетнаилучшее
локальное приближение
этой функции. Для этого оценим погрешность
приближения
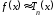 ,
т. е. оценим в некоторой окрестности
точки
,
т. е. оценим в некоторой окрестности
точки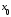 функцию
функцию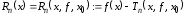 .
Разность
.
Разность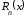 называютостаточным
членом
формулы
Тейлора.
называютостаточным
членом
формулы
Тейлора.
Покажем, что
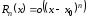 .
.
В самом деле, рассмотрим
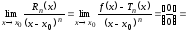 (применим
последовательно
(применим
последовательно
 раз правило Лопиталя) =
раз правило Лопиталя) =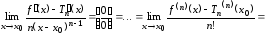
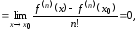 а это означает, что
а это означает, что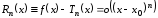 ,
,
т. е.
 . (4.19)
. (4.19)
Полученная
формула носит название формулы
Тейлора порядка
 функции
функции
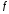 в точке
в точке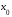 с остаточным
членом в форме Пеано.
Ее называют асимптотическим
разложением
с остаточным
членом в форме Пеано.
Ее называют асимптотическим
разложением
 -
го порядка функции
-
го порядка функции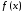 в окрестности точки
в окрестности точки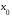 .
Формула (4.19) является качественной
характеристикой погрешности.
.
Формула (4.19) является качественной
характеристикой погрешности.
В
курсе математического анализа
доказывается, что можно найти и другие
погрешности приближения
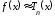 .
.
4.8. Формула Тейлора с остаточным членом в форме Лагранжа
Пусть
функция
 n
раз непрерывно дифференцируема на
n
раз непрерывно дифференцируема на
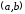 (т. е.
(т. е.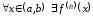 и эта функция непрерывна
и эта функция непрерывна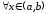 )и
имеет в каждой точке этого интервала,
за исключением, быть может, точки
)и
имеет в каждой точке этого интервала,
за исключением, быть может, точки
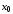 производную
производную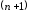 - го порядка. Тогда для любого
- го порядка. Тогда для любого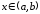 между
между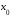 и
х
найдется такая точка
и
х
найдется такая точка
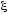 ,
что справедлива формула Тейлора
,
что справедлива формула Тейлора
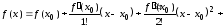 ...
...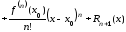 ,
(4.20)
,
(4.20)
где
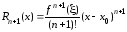 – остаточный
член в форме Лагранжа.
Так как точка
– остаточный
член в форме Лагранжа.
Так как точка
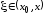 ,
то
,
то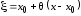 ,
где
,
где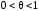 .
.
Формула (4.20) является количественной характеристикой погрешности.
Формула Маклорена11
Формулой
Маклорена
называется формула Тейлора при
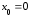 :
:
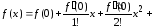 ...
...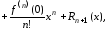
где
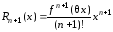 ,
,
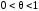 .
.
Пример
4.12. Разложить
функцию
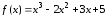 по степеням
по степеням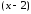 .
.
Решение.
 ,
,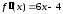 ,
,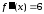 ,
,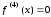 .
Отсюда
.
Отсюда
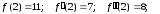
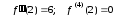 .
.
Следовательно, по формуле Тейлора третьего порядка
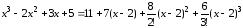 .
.
Остаточный
член
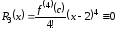 .
Таким образом,
.
Таким образом,
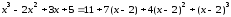 .
.
Пример
4.13. Разложить
функцию
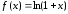 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки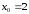 .
.
Имеем
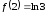 ,
,
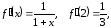
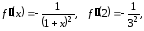
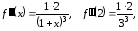 …,
…,
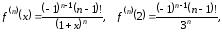
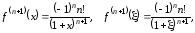 где
2 <
< x.
где
2 <
< x.
Поэтому
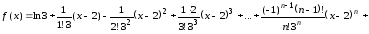
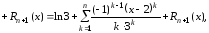
где
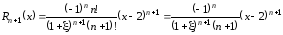 ,
,
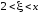 .
.
4.9. Разложения основных элементарных функций (асимптотические формулы)
Запишем
формулу Тейлора (4.19) при
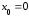 с остаточным
членом в форме Пеано:
с остаточным
членом в форме Пеано:
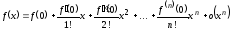 . (4.21)
. (4.21)
Формулу
(4.21) называют формулой
Маклорена
разложения функции
 по степеням
по степеням с
остаточным членом в форме Пеано.
с
остаточным членом в форме Пеано.
1.
Пусть
 .
Вычислим производные функции
.
Вычислим производные функции в точке
в точке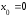 :
: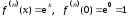 .
.
Используя формулу (4.21), получим
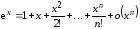 .
.
В
частности, при
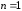 и
и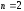 имеем:
имеем:
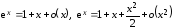 .
.
2.
Пусть
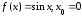 .
Вычислим значения производных функции
.
Вычислим значения производных функции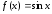 при
при :
:
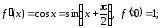
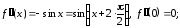
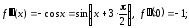
………………………………………………………………..
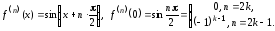
Используя
формулу (4.21) при
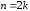 ,
находим:
,
находим:
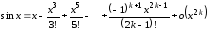 .
.
В
частности, при
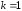 и
и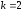 имеем:
имеем:
 .
.
3.
Разложение для
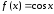 получается аналогично:
получается аналогично:
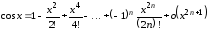 .
.
В
частности, при
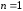 :
:
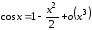 .
.
4.
Пусть
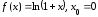 .
Вычислим значения производных функции
.
Вычислим значения производных функции при
при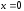 :
:
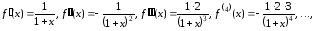
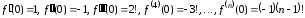
Тогда
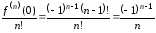 .
Используя формулу (4.21), получим:
.
Используя формулу (4.21), получим:
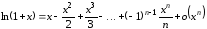 .
.
В
частности, при
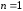
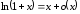 .
.
5. Аналогично получаем
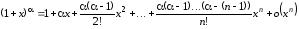 .
.
Если
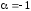 ,
то
,
то
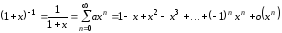 .
.
Заменив
 на
на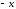 ,
получим:
,
получим:
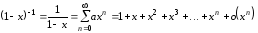 .
.
Пример
4.14. Разложить
функцию
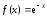 в ряд
Маклорена с точностью
в ряд
Маклорена с точностью
 .
.
Решение.
Воспользуемся разложением
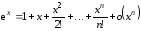 .
Заменим
.
Заменим на
на
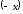 ,
получим
,
получим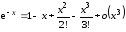 .
.
На
рисунке 4.6 изображена кривая
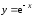 ,
а также ее приближения
,
а также ее приближения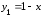 ,
,
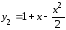 и
и
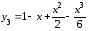 .
.
Пример
4.15. Разложить
функцию
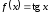 в окрестности точки
в окрестности точки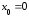 ,
взяв
,
взяв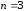 .
.
Решение.
Воспользуемся формулой Маклорена при
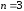 .
Найдем производные
.
Найдем производные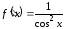 ,
,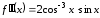 ,
,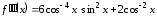 ,
отсюда
,
отсюда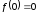 ,
,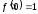 ,
,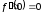 ,
, .
Получаем
.
Получаем
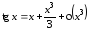 .
.
Пример
4.16. Используя
разложения функций по формуле Тейлора,
вычислить пределы: а)
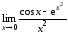 ;
б)
;
б)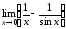 .
.
Решение. а) Воспользуемся разложениями:
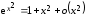 ,
,
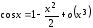 . Тогда
. Тогда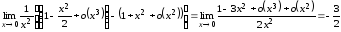 .
.
б)
Если ограничиться разложением
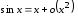 ,
то в пределе получаем выражение
,
то в пределе получаем выражение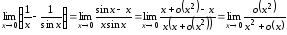 .
Чему равен такой предел, сказать
невозможно. Неизвестно, какие бесконечно
малые скрываются под
.
Чему равен такой предел, сказать
невозможно. Неизвестно, какие бесконечно
малые скрываются под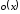 и
и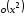 .
Поэтому следует взять приближение
.
Поэтому следует взять приближение
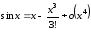 .
Тогда
.
Тогда
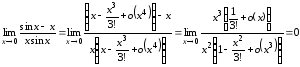 .
.
