- •Глава III. Дифференциальное исчисление функций нескольких переменных
- •3.1. Определение функции нескольких переменных
- •3.2. Предел функции нескольких переменных
- •3.3. Бесконечно малые функции нескольких переменных
- •3.4. Свойства пределов
- •3.5. Непрерывность функций нескольких переменных. Точки и линии разрыва
- •Свойства непрерывных функций
- •3.6. Частные приращения и частные производные функции нескольких переменных
- •3.9. Достаточные условия дифференцируемости функции нескольких переменных
- •3.10. Полный дифференциал функции нескольких переменных
- •3.10. 1. Применение полного дифференциала функции нескольких переменных для приближенных вычислений
- •3.11. Частные производные высших порядков
- •3.12. Дифференциалы высших порядков
- •3.13. Частные производные сложной функции нескольких переменных
- •3.14. Производная функции, заданной неявно
- •3.15. Производная функции по направлению
- •3.16. Градиент функции, его свойства
- •3.17. Формула Тейлора для функций двух переменных
- •3.18. Локальный экстремум функции нескольких переменных
- •3.19. Необходимый признак локального экстремума
- •3.20. Достаточный признак локального экстремума функции двух переменных
- •3.21. Метод наименьших квадратов (мнк)
- •3.22. Условный экстремум функции нескольких переменных
- •3.22.1. Постановка задачи
- •3.22.2. Нахождение критических точек
- •3.22.3. Метод множителей Лагранжа
- •3.22.4. Достаточный признак условного экстремума функции двух переменных
- •3.23. Абсолютный экстремум функций нескольких переменных
- •Вопросы к экзамену Введение в математический анализ
- •Дифференциальное исчисление функций одной переменной
- •Дифференциальное исчисление функций нескольких переменных
- •Литература Основная литература
- •Дополнительная литература
- •Шершнев Владимир Григорьевич математический анализ
- •Часть I. Дифференциальное исчисление
- •117997, Москва, Стремянный пер. 36.
Глава III. Дифференциальное исчисление функций нескольких переменных
3.1. Определение функции нескольких переменных
В практических задачах экономики, решаемых с использованием методов математического анализа, обычно функции зависят от нескольких переменных.
Например, в экономике часто используется функция Кобба-Дугласа
![]() ,
,
которая называется
производственной функцией. Эта функция
описывает зависимость объема производства
Q
от капитальных затрат К
и трудовых ресурсов L.
В этой функции А
(А >
0) – параметр производительности
конкретно взятой технологии,
![]() – доля капитала в доходе (0<
<1).
– доля капитала в доходе (0<
<1).
В экономических
задачах так же часто используется
функция
прибыли,
которая зависит от
![]() – объемов производства различных видов
продукции,
– объемов производства различных видов
продукции,
![]() – цен на единицы этих видов продукции
и затрат на производство
– цен на единицы этих видов продукции
и затрат на производство
![]() ,
,
где
![]()
функция затрат.
функция затрат.
Определение
функции нескольких переменных.
Переменная величина u
называется функцией переменных величин
![]() с областью определения D
и множеством значений E,
если любой точке М(
с областью определения D
и множеством значений E,
если любой точке М(![]() ),
принадлежащей области D,
соответствует единственное значение
u,
принадлежащее множеству Е.
),
принадлежащей области D,
соответствует единственное значение
u,
принадлежащее множеству Е.
Записывают
![]() (
(
![]() )
или u=
u(
)
или u=
u(![]() ).
).
Пример 3.1.
Найти область определения D
и множество значений Е
функции
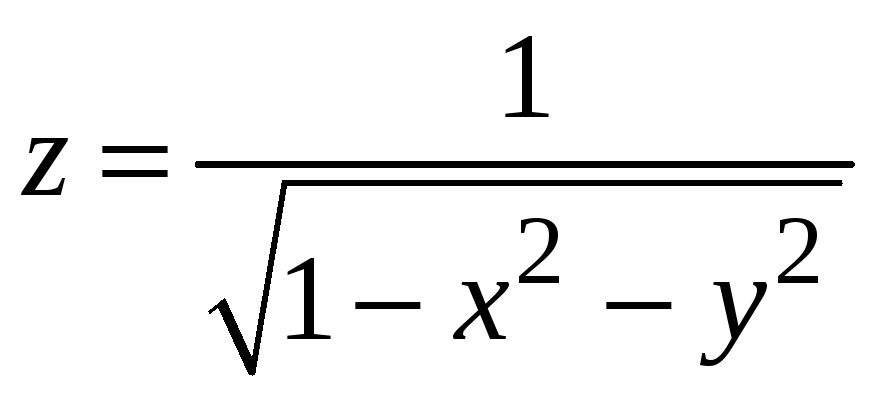 .
.
Находим
![]()
![]() ;
;
![]() .
.
Для простоты изложения обычно рассматривают функцию двух переменных. Обобщение результатов на большее число переменных не представляет труда.
Для изображения функции 2-х и 3-х переменных используют линии и поверхности уровня.
|
Рис. 46 |
Линией
уровня
функции
|
Поверхностью
уровня
функции 3-х переменных
![]()
![]() называ-ется множество точек
называ-ется множество точек
![]() трехмерного пространства
трехмерного пространства
![]() ,
в которых функция принимает постоянное
значение, т. е. f
,
в которых функция принимает постоянное
значение, т. е. f
![]() =
c,
с
= const.
=
c,
с
= const.
Например, для
функции
![]() поверхностями уровня являются сферы
поверхностями уровня являются сферы
![]() r
= const.
r
= const.
3.2. Предел функции нескольких переменных
Определение
предела
функции нескольких переменных по Коши
на языке «![]() ».
Число b
называется пределом функции
».
Число b
называется пределом функции
![]() при
при
![]() ,
,
![]() ,
если для любого
больше нуля существует такое ,
зависящее от ,
что если х
принадлежит -окрестности
,
если для любого
больше нуля существует такое ,
зависящее от ,
что если х
принадлежит -окрестности
![]() ,
y
принадлежит -окрестности
,
y
принадлежит -окрестности
![]() ,
то значение функции
,
то значение функции
![]() принадлежит -окрестности
числа b.
принадлежит -окрестности
числа b.
С помощью кванторов данное определение можно записать так
![]()
![]() ,
,
![]()
![]() .
.
Множество точек плоскости Oxy, удовлетворяющее неравенству
![]() ,
,
называется
-окрестностью
точки
![]() .
.
Записывают
![]() ,
где
,
где
![]()
расстояние между точками
расстояние между точками
![]() и М,
и М,
![]() .
.
Учитывая это, определение предела функции можно записать следующим образом
![]() .
.
Можно также записать по другому,
![]() .
.
Определение предела
функции нескольких переменных при
![]() имеет вид
имеет вид
![]() .
.
Нахождение пределов функций нескольких переменных сводится к нахождению пределов функций одной переменной.
Пример 3.2.
Найти предел
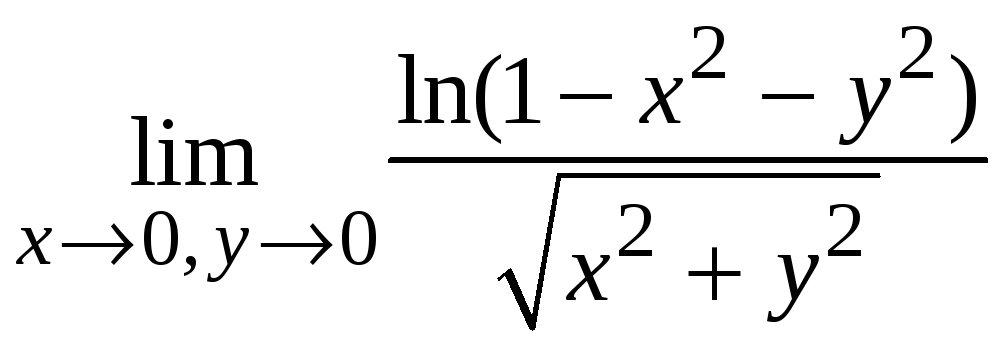 .
.
Сделаем замену переменной, получим предел функции одной переменной и применим правило Лопиталя.
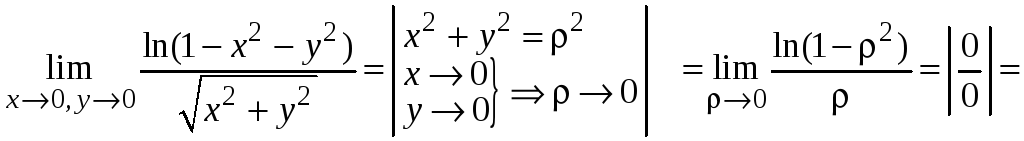
 .
.
Пример
3.3. Показать,
что
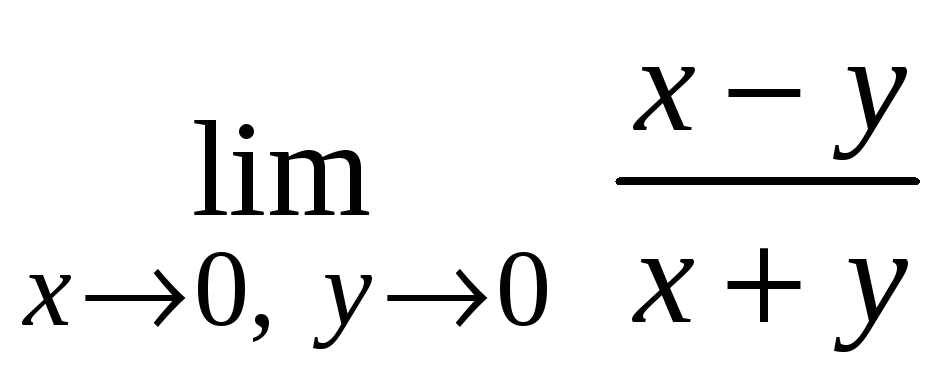 не существует.
не существует.
Найдем этот предел
при двух способах стремления
![]() к
к
![]() .
.
-
Если
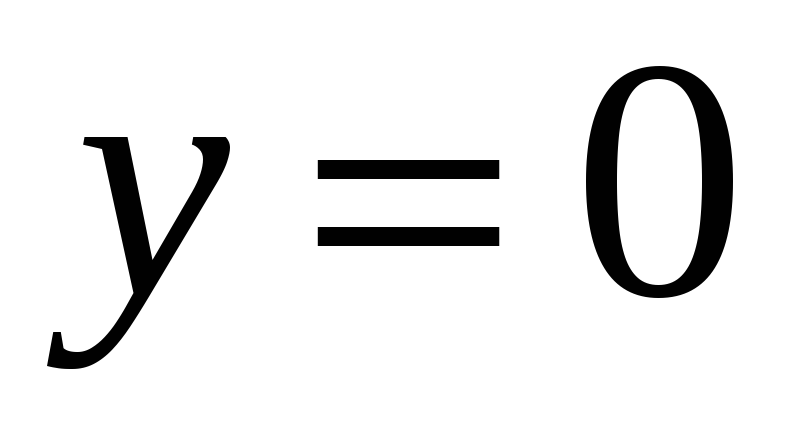 ,
а
,
а
 ,
то
,
то
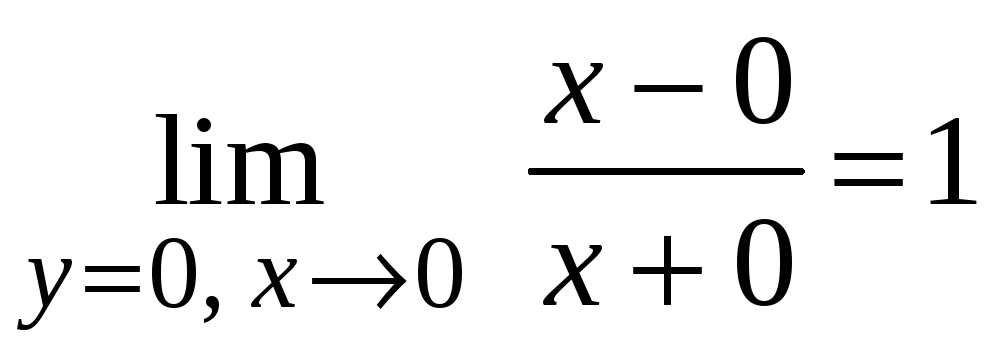 .
. -
Если
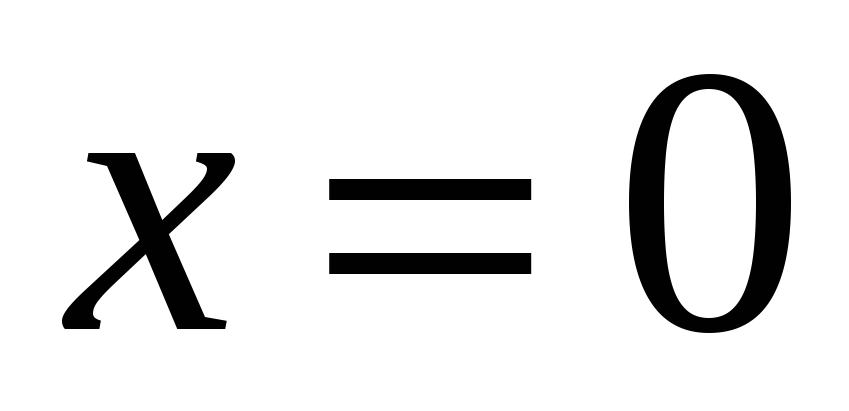 ,
а
,
а
 ,
то
,
то
 .
.
При различных
способах стремления точки
![]() к точке
к точке
![]() предел имеет различные значения,
следовательно, он не существует.
предел имеет различные значения,
следовательно, он не существует.