3.3. Бесконечно малые функции нескольких переменных
Запишем определения бесконечно малой и бесконечно большой функций нескольких переменных.
Функция нескольких
переменных
называется бесконечно малой функцией
при
,
если
.
Запишем более подробно с помощью кванторов.
.
Функция называется
бесконечно большой при
,
если ее предел не ограничен.
.
Для функций нескольких переменных, так же, как и для функций одной переменной, функция обратная к бесконечно малой является бесконечно большой и, наоборот, функция обратная к бесконечно большой является бесконечно малой.
Бесконечно малые функции нескольких переменных обладает такими же свойствами, что и бесконечно малые функции одной переменной.
3.4. Свойства пределов
Пределы функций нескольких переменных обладают такими же свойствами, как и пределы функций одной переменной.
Теорема 3.1. Если
функции
и
имеют одинаковые области определения
и имеют конечные пределы при
и
,
где
b
= const, c
= const,
то справедливы следующие соотношения:
1)
;
2)
;
3)
,
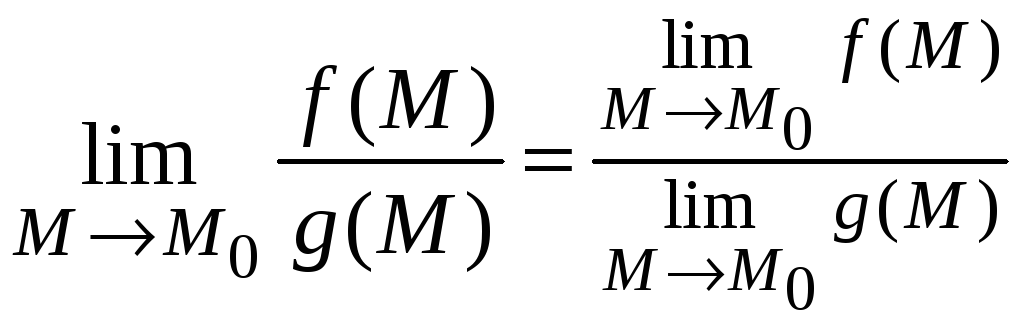если
.
3.5. Непрерывность функций нескольких переменных. Точки и линии разрыва
Полным приращением
функции нескольких переменных
в точке
называется разность значений функции
и
,
т. е.
.
Если функция
зависит от двух переменных
,
то
.
Определение 1.
Функция
называется непрерывной в точке
,
если она определена в окрестности этой
точки и бесконечно малым приращениям
независимых переменных соответствует
бесконечно малое приращение функции,
т. е.
.
Пример 3.4.
Показать, что функция
является непрерывной в любой точке
плоскости Oxy.
Находим
.
Преобразуем предел
.
.
Следовательно,
или
,
т. е. предел функции равен функции от предела независимой переменной.
Определение 2.
Функция
называется непрерывной в точке
,
если она определена в окрестности этой
точки и
.
Можно записать с помощью кванторов на языке «».
.
Функции нескольких
переменных, как и функции одной переменной,
могут иметь точки разрыва. Точка
называется точкой разрыва функции
нескольких переменных, если функция не
является непрерывной в этой точке.
Например, функция
имеет точку разрыва O(0,
0).
Функции нескольких
переменных могут иметь линии разрыва.
Например,
имеет две линии разрыва в виде
пересекающихся прямых
;
а функция
имеет линию разрыва в виде параболы
.
Свойства непрерывных функций
1. Если функция нескольких переменных является непрерывной в замкнутой области, то она достигает в этой области своего наибольшего и наименьшего значений.
2. Если функция нескольких переменных является непрерывной в замкнутой области, то она хотя бы один раз принимает в этой области любое значение между своим наименьшим и наибольшим значениями.
3. Если функция непрерывна в замкнутой области, то она равномерно-непрерывная в этой области.
Функция
называется равномерно-непрерывной в
некоторой области, если для любого
> 0 существует такое ()
> 0, что для любых двух точек
и
этой области, расстояние между которыми
меньше
(
) выполняется неравенство
.