Глава 5. Определенный интеграл

5.1. Задачи, приводящие к понятию определенного интеграла

Рассмотрим две задачи, одна с геометрическим смыслом, другая с механическим смыслом.

1. Задача о площади криволинейной трапеции.

Пусть функция является непрерывной на отрезке . Требуется найти площадь криволинейной трапеции, ограниченной линиями: , (рис. 57).

Рис. 57

При нахождении площади этой трапеции выполним следующие действия:

1. Разобьем отрезок [a, b] с помощью произвольно выбранных точек

на n элементарных отрезков длиной

.

2. На каждом элементарном отрезке выберем произвольно точку , вычислим значение функции в этой точке и найдем приближенно площадь элементарной криволинейной трапеции как площадь прямоугольника .

3. Найдем приближенно площадь всей криволинейной трапеции

.

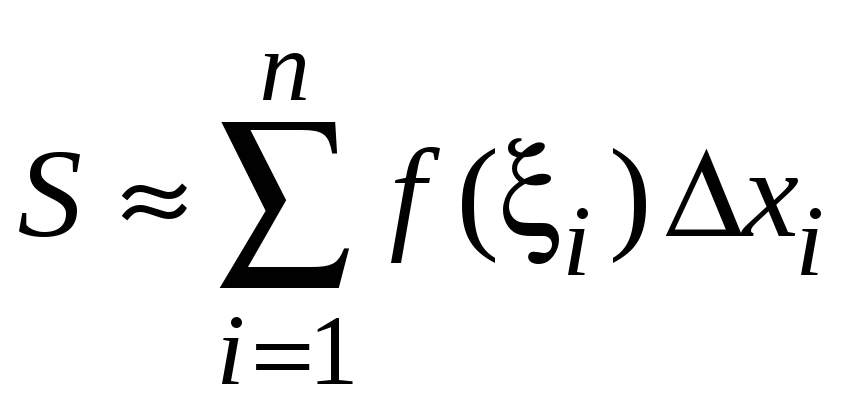4. Перейдем к пределу при , найдем точное значение площади криволинейной трапеции

.

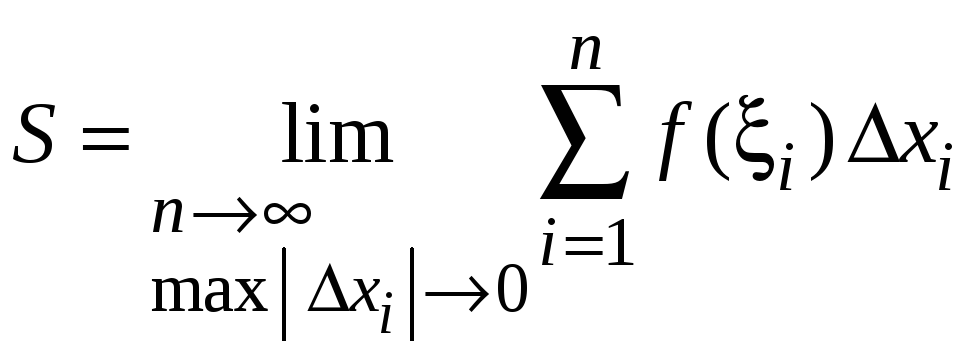2. Задача о пройденном пути.

Пусть известна зависимость скорости движения от времени на отрезке времени .Требуется найти длину пути, пройденного за время от до Т.

1. Разобьем отрезок времени с помощью произвольно выбранных моментов времени

на n элементарных интервалов времени продолжительностью

, i = 1, 2, …, n.

2. На каждом элементарном интервале времени выберем произвольно момент времени , вычислим скорость и найдем приближенно путь пройденный за элементарный интервал времени

, i = 1, 2, …, n.

3. Найдем приближенно путь, пройденный за отрезок времени ,

.

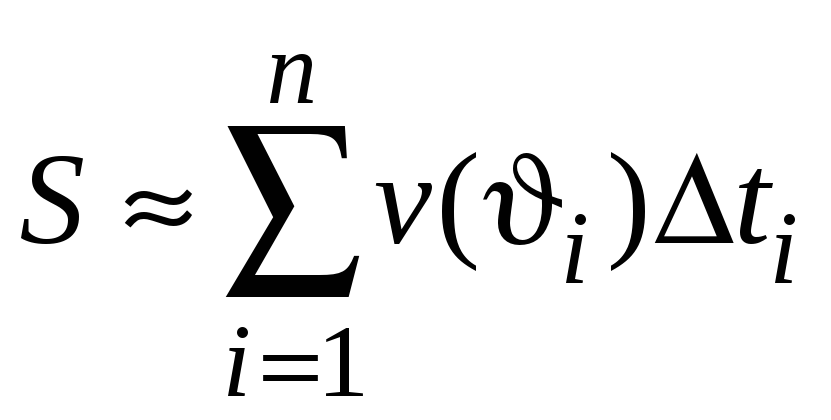4. Перейдем к пределу при , найдем точное значение пройденного пути

.

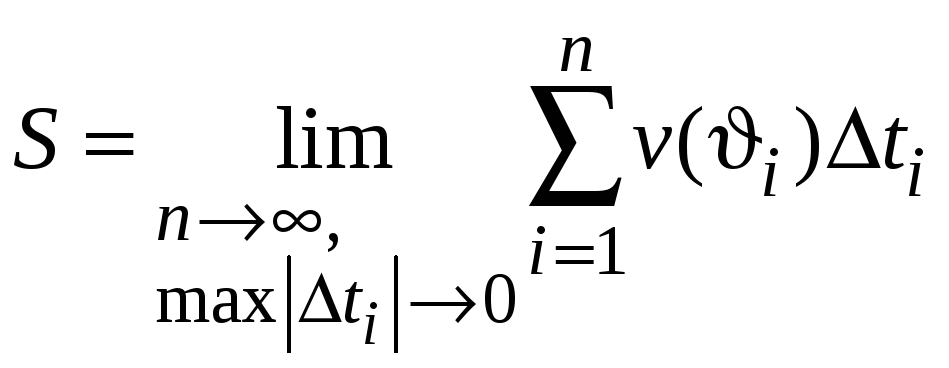Как можно заметить, в рассмотренных задачах с геометрическим и механическим смыслом, решение выполняется в аналогичном порядке. Поэтому можно выполнить подобные действия независимо от прикладного смысла задачи. Обобщим полученные результаты.

5.2. Интегральные суммы, их свойства

Пусть функция является непрерывной на отрезке . Разобьем отрезок с помощью произвольно выбранных точек

на n элементарных отрезков длиной

.

Функция является непрерывной, поэтому на каждом элементарном отрезке достигает своего наименьшего и наибольшего значений

, .

Составим две суммы следующего вида

и .

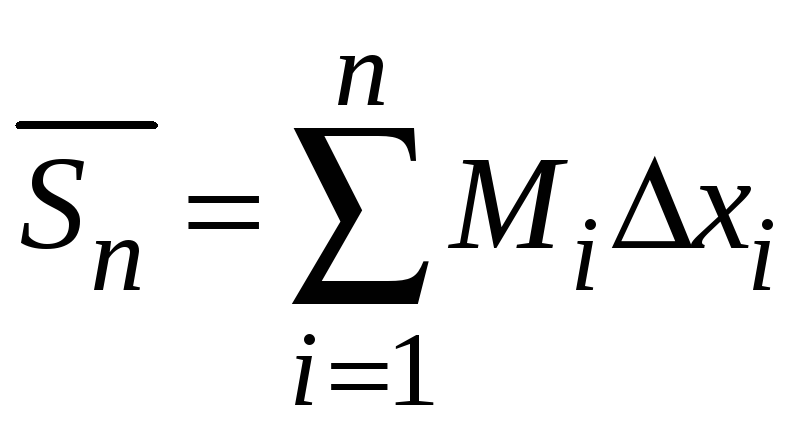Данные суммы называются  нижней,  верхней интегральными суммами Дарбу. Очевидно, что

,

где , .

Свойство 1. При увеличении числа точек разбиения отрезка на элементарные отрезки нижняя интегральная сумма возрастает, а верхняя убывает.

Д о к а з а т е л ь с т в о. Рассмотрим один элементарный отрезок длиной h (рис. 58). Разобьем этот отрезок на два длиной и , . Пусть и наименьшее и наибольшее значения функции на первом и втором отрезке соответственно.

Рис. 58

Пусть для определенности . Нижняя интегральная сумма на исходном элементарном отрезке . Нижняя интегральная сумма на этом элементарном отрезка после разбиения на две части . Можно записать

, т. е. .

Аналогично, если , то

, т. е. .

Следовательно, при увеличении числа элементарных отрезков нижняя интегральная сумма Дарбу возрастает, а верхняя убывает.

Свойство 2. Нижняя и верхняя интегральные суммы Дарбу имеют пределы при и .

Д о к а з а т е л ь с т в о. Очевидно .

Пусть число точек деления отрезка на элементарные возрастает, т.е. . Соответствующие нижние интегральные суммы монотонно возрастают и ограничены . По теореме Вейерштрасса последовательность этих сумм имеет предел

.

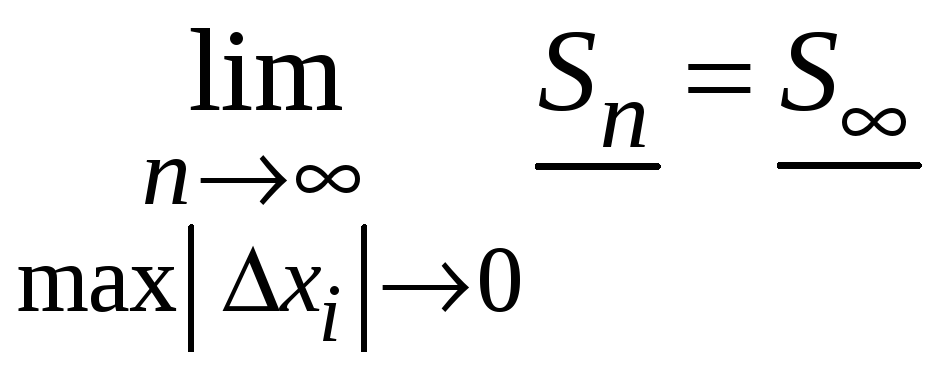Последовательность верхних интегральных сумм при увеличении числа точек деления монотонно убывает и ограничена снизу . Поэтому она также имеет предел

.

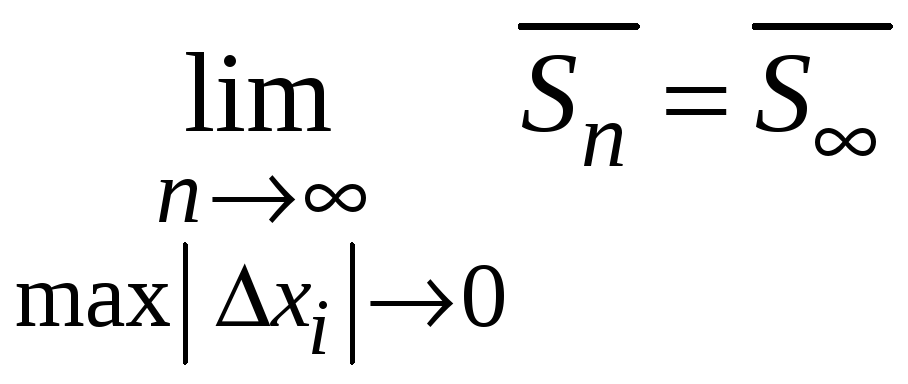Свойство 3. Пределы нижней и верхней интегральных сумм при и совпадают.

Д о к а з а т е л ь с т в о. Найдем разность верхней и нижней интегральных сумм

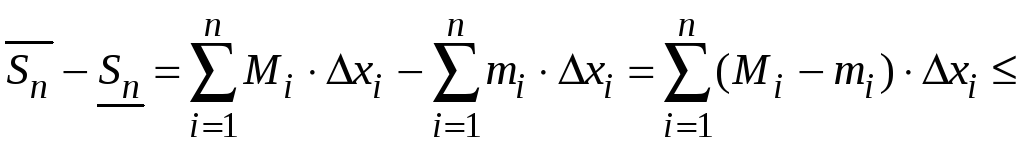
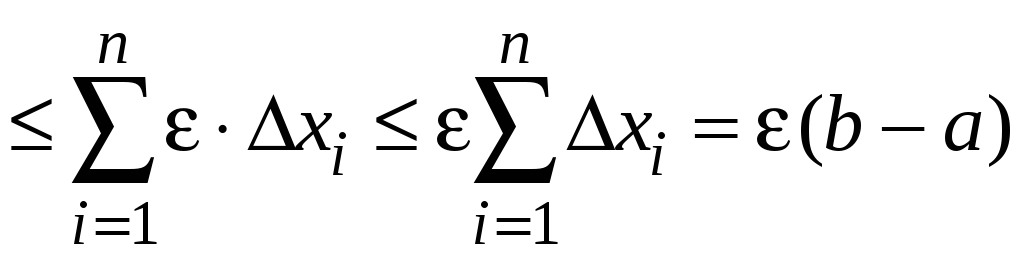, где .

Так как функция непрерывна на отрезке , то она и равномерно непрерывна на этом отрезке.

Тогда для любого положительного существует такое , что если , то .

Следовательно,

.

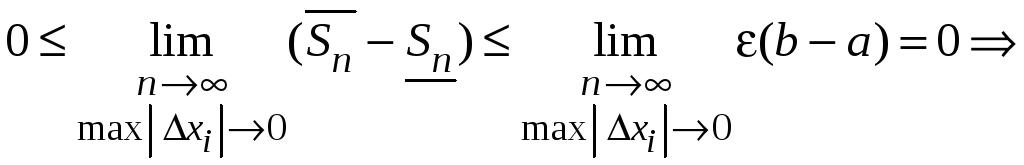
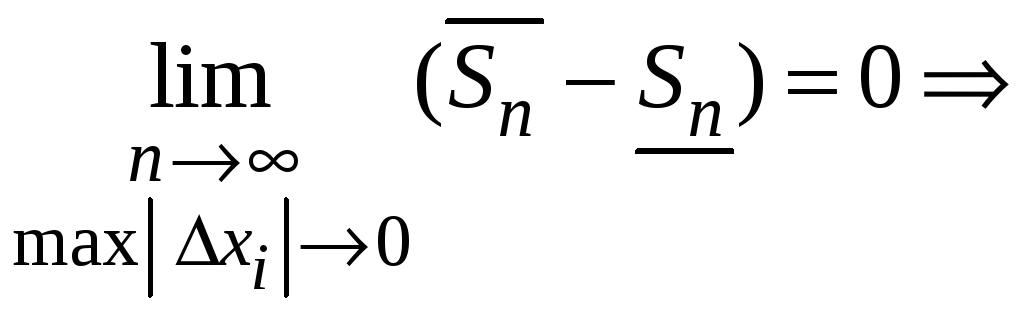
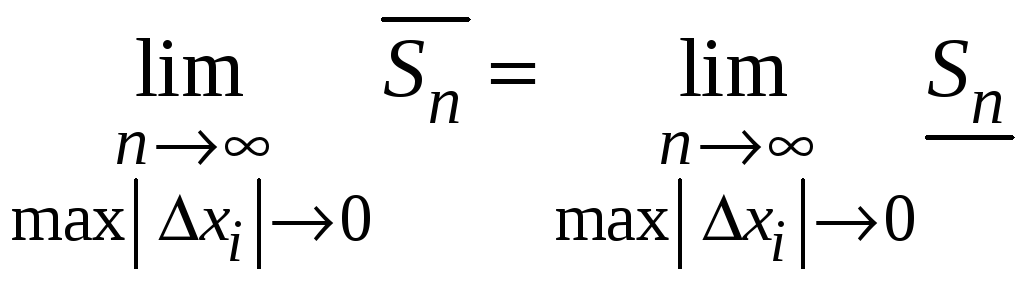Свойство 4. Для любой непрерывной на отрезке функции при любом способе разбиения на элементарные отрезки интегральные суммы имеют один и тот же предел, если .

Д о к а з а т е л ь с т в о. Используем теорему о промежуточной функции. Так как для любой интегральной суммы ,

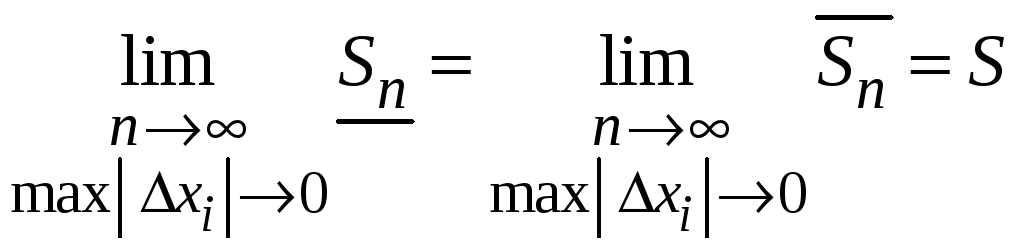, то .
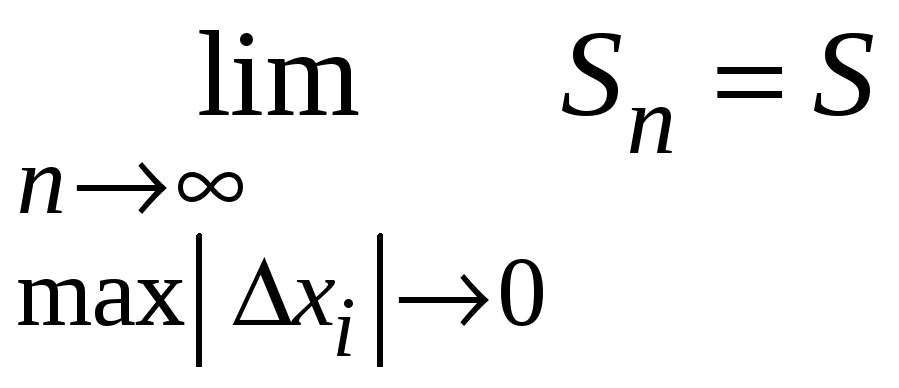