лекции мат. анализ

Российский Экономический Университет им. Плеханова

Воронежский филиал

Конспект лекций, примеры решения задач и задания на контрольную работу по дисциплине

Математический

анализ

Разработал: доцент Моисеев Сергей Игоревич

Воронеж, 2014 г.

1

Тема 1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

1.1. Понятие множества

Множество — первичное понятие математики. Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит и не имеющее определения. Однако, существуют различные описания множества. Например, Георг Кантор дал такое описание: Под «множеством» мы понимаем соединение в некое целое определенных хорошо различимых предметов нашего созерцания или нашего мышления, которые будут называться «элементами» множества.

Другая формулировка принадлежит Бертрану Расселлу: «Множество суть совокупность различных элементов, мыслимая как единое целое». Основоположником теории конечных и бесконечных множеств был Бернард Больцано. Позднее, в 1872-1884 гг., Георг Кантор систематически изложил основы теории множеств. Он не только ввѐл основные понятия теории множеств, но и обогатил математику рассуждениями нового типа, которые применил для доказательства теорем теории множеств, в частности впервые к бесконечным множествам. Поэтому общепризнано, что теорию множеств создал Георг Кантор.

В настоящее время, общепринято следующее определение. Множество - это совокупность, класс отличающихся друг от друга

объектов, объединенных каким-либо общим свойством. Объекты, входящие в эту совокупность, называются элементами множества.

Множества обозначаются заглавными буквами латинского алфавита, а элементы множества - строчными.

Примерами множеств являются: множество студентов данного вуза, множество предприятий некоторой отрасли, множество натуральных чисел и т.п.

Студенты одной группы – множество, элементы которого - студенты, общее свойство – обучение одной специальности.

Множество – корни уравнения . Элементы – вещественные числа, общее свойство – обращают данное уравнение в верное равенство.

Если	– элемент множества	, то говорят:	принадлежит и пи-
шут:	. Если не принадлежит	, то пишут	.

Множества могут быть конечными, бесконечными, пустыми, универсальными, неупорядоченные, упорядоченные; счетные и несчетные.

2

Множество называется конечным, если оно состоит из конечного числа элементов, в противном случае оно называется бесконечным.

Множество, не содержащее ни одного элемента, называется пустым и обозначается Ø.

Множество называется счетным, если его элементы можно пересчитать, т.е. занумеровать натуральными числами; и несчетным в противном случае. Например, множества натуральных, целых, рациональных чисел – счетные, а множество действительных (вещественных) чисел – несчетное.

Существует два основных способа задания множеств: перечисление всех его элементов; описание характеристического (общего) свойства

его элементов.
Первым способом задаются конечные множества.
Примеры:
– множество чисел, являющихся делителями числа	:

– список группы:

Вторым способом можно задать конечные, бесконечные, пустые множества. Множество элементов, обладающих характеристическим

свойством , обозначается:	и читается так: множество всех х
таких, что х обладает свойством	.
Примеры:

–- это конечное множество и его можно за-

дать перечислением элементов: {2, -2}.

– бесконечное несчетное множество, а имен-

но, числовой промежуток

– это пустое множество, т.к. ни одно вещественное число не удовлетворяет данному уравнению.

1.2. Операции над множествами

Если каждый элемент множества			принадлежит множеству			, то
называют подмножеством множества			. Обозначения:		(	при-
надлежит ,		включено в , содержится в		и т.д.),
Пример.		– множество натуральных чисел, – множество четных
чисел, тогда		.
Множества		называются равными,		если	.	Обо-
значение:		.
Пример.				Данные множества
равны	, действительно:

3

Если – универсальное множество некоторой теории, то любое множество этой теории является его подмножеством. Например, множество комплексных чисел – универсальное множество в теории чисел. Для всех классов чисел можно построить цепочку включений:

N Z Q R C.

Свойства включений.

1.Для всякого множества

2.Для любых множеств

3.Для всякого множества

Над множествами можно выполнять действия (операции), напоминающие сложение и умножение чисел, но не тождественные им.

Объединением (суммой) множеств и называется множество, обозначаемое через , содержащее те и только те элементы, которые принадлежат множеству А или В.

Краткая запись: Пример:

Пересечением (произведением) множеств			называется множе-
ство,	обозначаемое через	и состоящее из тех и только из тех эле-
ментов, которые принадлежат множеству А и множеству В.
Краткая запись:		.
Пример:
Разностью множеств		называется множество, обозначаемое
через	и состоящее из тех и только из тех элементов, которые при-

надлежат и не принадлежат .
Краткая запись:		.
Пример:			.
Если
Если – универсальное множество и			, то разность	назы-
вается дополнением множества		до множества .
Симметрической разностью		множеств	называется	множе-
ство, обозначаемое	и состоящее из тех и только из тех элементов,
которые принадлежат	или	.
Краткая запись:			.
Пример:			.

1.3. Числовые множества

Множество, элементами которого являются числа, называется чис-

ловым.

4

Основные числовые множества.

–множество натуральных чисел.

–множество целых неотрицательных чисел.

–множество целых чисел.

{} – множество рациональных чисел.

Действительные числа (R), не являющиеся рациональными, называются иррациональными (I).

Геометрически множество действительных чисел R изображается точками числовой прямой (числовые оси). (Рис.1.1.), т.е. прямой, на которой выбрано начало отчета, положительное направление и единица масштаба.

0	1	Рис.1.1.	х

Между множеством вещественных чисел и точками числовой прямой существует взаимно однозначное соответствие, т.е. каждому действительному числу соответствует определенная точка числовой прямой, и наоборот, каждой точке прямой – определенное вещественное число.

Пусть a и b—действительные числа, причем a<b.

Числовыми промежутками (интервалами) называют подмножества всех действительных чисел, имеющих следующий вид:

[a; b] = {х: α ≤ х ≤ b} — отрезок (сегмент, замкнутый промежуток); (a; b) = {х: а < х < b} — интервал (открытый промежуток);

[a;b) = {х: а ≤ х < b}; (a; b] = {х: а < х ≤ b} — полуоткрытые интер-

валы (или полуоткрытые отрезки);

(-∞; b] = {х: х ≤ b}; [а, +∞) = {х: х ≥ а }; (-∞; b) = {х: х <b};

(а, +∞) = {х: х > а}; (-∞, ∞) = {х: -∞<х<+∞} = R - бесконечные ин-

тервалы (промежутки).

Числа a и b называются соответственно левым и правым концами этих промежутков. Символы -∞ и +∞ не числа, это символическое обозначение процесса неограниченного удаления точек числовой оси от начала 0 влево и вправо.

1.4. Понятие функции

Понятие функции является одним из основных в математике. С его помощью выражают зависимости между различными переменными величинами. Изучение свойств функций, основанное на методе пределов, составляет основное содержание математического анализа.

5

При изучении различных явлений природы, а также при решении экономических, инженерных, технических задач мы замечаем, что одни величины сохраняют одно и то же численное значение, а другие величины связаны между собой определенной зависимостью.

Величины первого вида принято называть постоянными. Примерами таких величин могут служить: отношение длины окружности к своему диаметру (число π), отношение диагонали квадрата к его сто-

роне, равное √ , и др.

Примерами величин другого типа могут служить: 1) зависимость площади круга от его радиуса , где - площадь круга, - радиус круга; 2) величина заработка рабочего при сдельной оплате труда зависит от фактической выработки и др.

Следует заметить, что радиус круга , фактическая выработка рабочего не могут быть отрицательными величинам и каждому значению этих величин соответствует значение площади круга, в первом примере и величина заработка - во втором.

Обобщая эти примеры, можно получить следующие определе-

ния.

Определение функции. Если каждому элементу из множества по некоторому правилу (закону) ставится в соответствие единственный элемент другого множества , то говорят, что между элементами (переменными) и y существует функциональная зависимость; при этом переменную величину называют независимой переменной, или аргументом, а переменную величину – зависимой переменной, или

функцией.

В приведенных выше примерах площадь круга S есть функция аргумента ; заработок при сдельной оплате труда есть функция производительности труда рабочего.

Функцию обозначают некоторым символом,			например f , и
пишут
y f (x),	x X
X называется областью определения функции			f , x - ее аргу-
ментом, а y - значением функции в точке x .
Областью определения функции	y f (x )	называется множе-
ство значений аргумента x , при которых функция		f (x ) имеет смысл
(существует). Обозначается D(y).

Используются также обозначения: D( f ) для области определения и E( f ) для множества значений функции.

6

		Если функция задана аналитически,					то при нахождении D(y)
учитывают следующее:
1)	2n g(x ) (n N ) существует, если g(x ) 0 ;
2)		g(x )			существует, если (x ) 0 и x		D(g)		D( ) ;
		(x )
3)	log			u (x )		v(x ) существует, если v(x ) 0, u(x ) 0, u(x ) 1;
4)	arcsin u(x ), arccos u(x ) существуют, если								u(x )		1;
5) если					f (x ) f1(x ) f2 (x ) , то D( f ) D( f1) D( f2 ) .

Примеры.

1) Для функции y 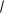x область определения и множество значений имеют вид: D( f ) [0, ) , E( f ) [0, ) ; график функции представ-

лен на рис. 2.1.			Рис. 2.1.
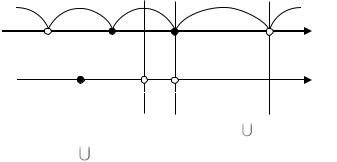
				E( f ) [0,1] ;
2) Для функции y	1 x2 имеем		D( f ) [ 1, 1] ,
график функции изображен на рис. 2.2.

Рис. 2.2.

	3) Для функции	1			имеем: D( f ) ( , 1)	(1, ) ,
		y x 1

7

E( f ) ( , 0) (0, ) ; ее график приведен на рис. 2.3.

Рис. 2.3.

Задача1.

Найти

области

определения

функции:

y ar csin

1 4x

3

Решение

1 4x

1 4x

1

1

4x 1

3 3 4x 1 3

3

3

1

2 4x 4

x 1.

2

Ответ:

1

.

D(y)

;1

2

Задача 2. Найти области определения функции:

y

x 2

1

log x (x 2)

(x

3)(x

4)

Решение

(x 1)(x 1)

0,

x 2 1

(x 3)(x 4)

0,

3,

4)

(x 3)(x

x

4)

0,

4,

x

(x 3)(x

0,

x 2

x 2,

x 0,

0,

x 1

x

1.

x

Решим системы неравенств.

8

Первая система +	-	+		-	+
	-3	-1		1	4
Вторая система
	-2			1
			Рис.02.4.
Пересечением решений является множество 0;1					4;
Ответ: D(y) 0;1		4; .

1.5. Способы задания функции

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции. Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ. Графиком функции y f (x ) называется

множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В экономике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геомет-

9

рическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Этот способ дает возможность по каждому численному значению аргумента найти соответствующее ему численное значение функции точно или с некоторой точностью. Если зависимость между и y задана формулой, разрешенной относительно , то есть имеет вид , то говорят, что функция от задана в явном виде. Если же

значения и связаны некоторым уравнением вида , то есть формула не разрешена относительно , что говорят, что функция задана неявно. Функция может быть определена разными

формулами на разных участках области своего задания. Аналитический способ является самым распространенным спо-

собом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа - основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.

Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

Пример 1: Функция	- целая часть числа . Обозна-
чает наибольшее из целых чисел, которое не превышает .
Пример 2: Функция	- дробная часть числа.
	- целая часть числа .

Основными недостатками словесного способа задания функции являются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. Главное преимущество же заключается в возможности задания тех функций, которые не удается выразить аналитически

1.6.Свойства функций

1. Четность функции.

При исследовании функций бывает полезно знать, как влияет перемена знака аргумента на значение функции. В связи с этим выделяются четные и нечетные функции.

10