Глава 8. Числовые ряды

8.1. Основные понятия

8.1. 1. Определение числового ряда

Множество чисел перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров называется числовой последовательностью

.

Числовым рядом называется сумма членов бесконечной числовой последовательности

.

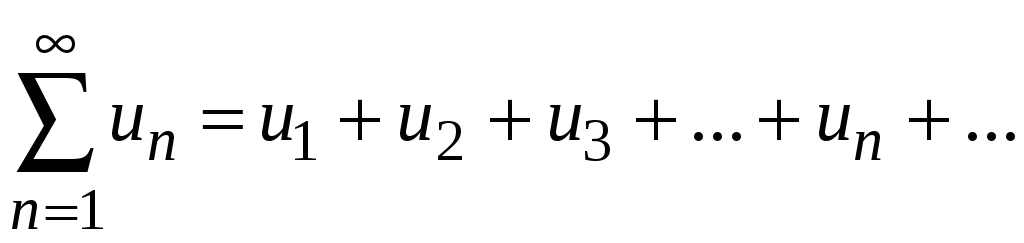Ряд считается заданным, если известен закон образования n-го (общего) члена ряда в зависимости от его номера. Обычно общий член ряда задается как функция или .

Например: 1) если , то ;

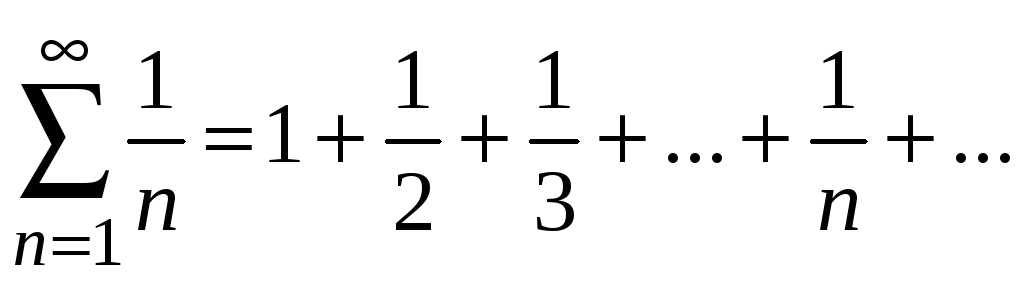2) если , то ;

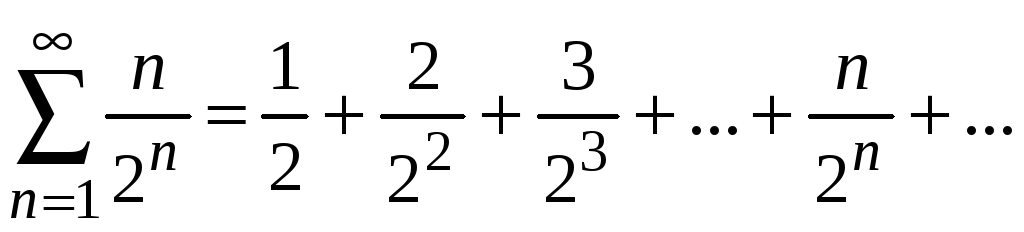3) если , , то

.

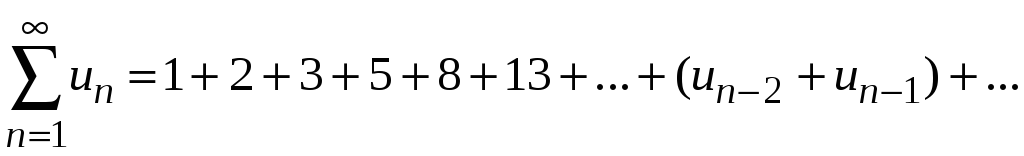Обычно, при исследовании числовых рядов возникает необходимость нахождения вида общего члена ряда как функции от номера этого члена. Для этого нужно перенумеровать члены ряда и, учитывая четность, периодичность и другие особенности его членов записать функцию .

	+	+	+	…. +	+ …
n	1	2	3		n

Например: 1)

Числитель каждого следующего члена этого ряда на 2 больше, а знаменатель на 3 больше, поэтому в n-ом члене ряда нужно записать в числителе 2n , а в знаменателе 3n. Кроме того, в числителе нужно к 2n прибавить 1, а в знаменателе к 3n прибавить 2, чтобы при n = 1 . Тогда .

	+	+	+	…. +	+ …
n	1	2	3		n

2)

Числители являются степенями числа 3, а в знаменателях находится факториалы номеров членов n, .

8.1.2. Сходимость числового ряда. Сумма ряда

В прикладных задачах, как правило, требуется найти сумму ряда. Ряд представляет собой бесконечную сумму, поэтому найти точное значение суммы ряда, обычно, не представляется возможным. Однако сумму ряда можно найти приближенно, если есть уверенность, что она существует. Дело в том, что сумма ряда даже с очень малыми членами может быть бесконечно большой или вообще не существовать. Поэтому основная трудность при нахождении суммы ряда заключается в том, чтобы доказать, что она существует.

Числовой ряд разделяют на две части

.

Сумма первых n членов ряда называется n-ой частичной суммой ряда

.

Сумма всех членов ряда, начиная с (n+1)-го, называется n-ым остатком ряда

.

Ряд называется сходящимся, если существует предел последовательности n-ых частичных сумм ряда

.

Если предел частичных сумм не существует, ряд называется расходящимся.

Если ряд сходится, то предел частичных сумм ряда называется суммой ряда, т. е. .

Пример 8.1. Исследовать сходимость ряда, являющегося геометрической прогрессией

,

где b  первый член прогрессии, q  знаменатель прогрессии.

Известно, что n -я частичная сумма этого ряда равняется

.

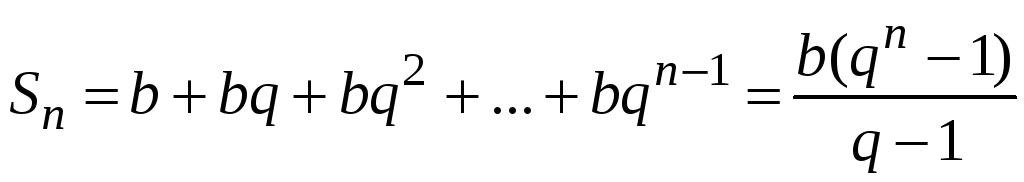В зависимости от величины знаменателя прогрессии q возможны 4 случая.

1. Если , то

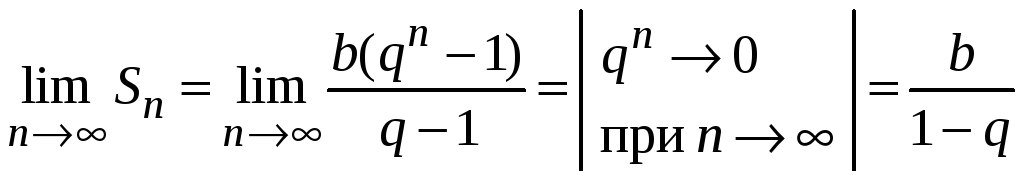
является конечной величиной и, следовательно, ряд сходится.

2. Если , то

является бесконечно большой величиной и, следовательно, ряд расходится.

3. Если , то

является бесконечно большой величиной и, следовательно, ряд расходится.

4. Если , то

Следовательно, предел не существует и ряд расходится.