- •Глава III. Дифференциальное исчисление функций нескольких переменных
- •3.1. Определение функции нескольких переменных
- •3.2. Предел функции нескольких переменных
- •3.3. Бесконечно малые функции нескольких переменных
- •3.4. Свойства пределов
- •3.5. Непрерывность функций нескольких переменных. Точки и линии разрыва
- •Свойства непрерывных функций
- •3.6. Частные приращения и частные производные функции нескольких переменных
- •3.9. Достаточные условия дифференцируемости функции нескольких переменных
- •3.10. Полный дифференциал функции нескольких переменных
- •3.10. 1. Применение полного дифференциала функции нескольких переменных для приближенных вычислений
- •3.11. Частные производные высших порядков
- •3.12. Дифференциалы высших порядков
- •3.13. Частные производные сложной функции нескольких переменных
- •3.14. Производная функции, заданной неявно
- •3.15. Производная функции по направлению
- •3.16. Градиент функции, его свойства
- •3.17. Формула Тейлора для функций двух переменных
- •3.18. Локальный экстремум функции нескольких переменных
- •3.19. Необходимый признак локального экстремума
- •3.20. Достаточный признак локального экстремума функции двух переменных
- •3.21. Метод наименьших квадратов (мнк)
- •3.22. Условный экстремум функции нескольких переменных
- •3.22.1. Постановка задачи
- •3.22.2. Нахождение критических точек
- •3.22.3. Метод множителей Лагранжа
- •3.22.4. Достаточный признак условного экстремума функции двух переменных
- •3.23. Абсолютный экстремум функций нескольких переменных
- •Вопросы к экзамену Введение в математический анализ
- •Дифференциальное исчисление функций одной переменной
- •Дифференциальное исчисление функций нескольких переменных
- •Литература Основная литература
- •Дополнительная литература
- •Шершнев Владимир Григорьевич математический анализ
- •Часть I. Дифференциальное исчисление
- •117997, Москва, Стремянный пер. 36.
3.21. Метод наименьших квадратов (мнк)
При решении экономических задач часто возникает необходимость представления опытных данных в аналитическом виде. Наиболее известным математическим методом для этих целей является метод наименьших квадратов.
Пусть имеются опытные данные в виде таблицы
|
|
|
|
|
|
из двух строк, в
первой строке которой находятся значения
некоторой переменной, принимаемой за
независимую, а во второй соответствующие
значения другой переменной, принимаемой
за функцию. Требуется найти аналитическую
функциональную зависимость
![]() .
.
Наиболее просто найти аналитическую зависимость возможно с помощью интерполяционного многочлена Лагранжа, который в общем виде записывается следующим образом
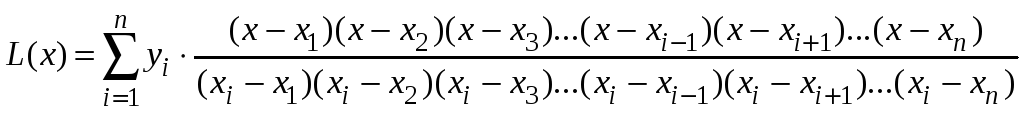 .
.
График данной функции проходит совершенно точно через заданные точки (рис. 50).
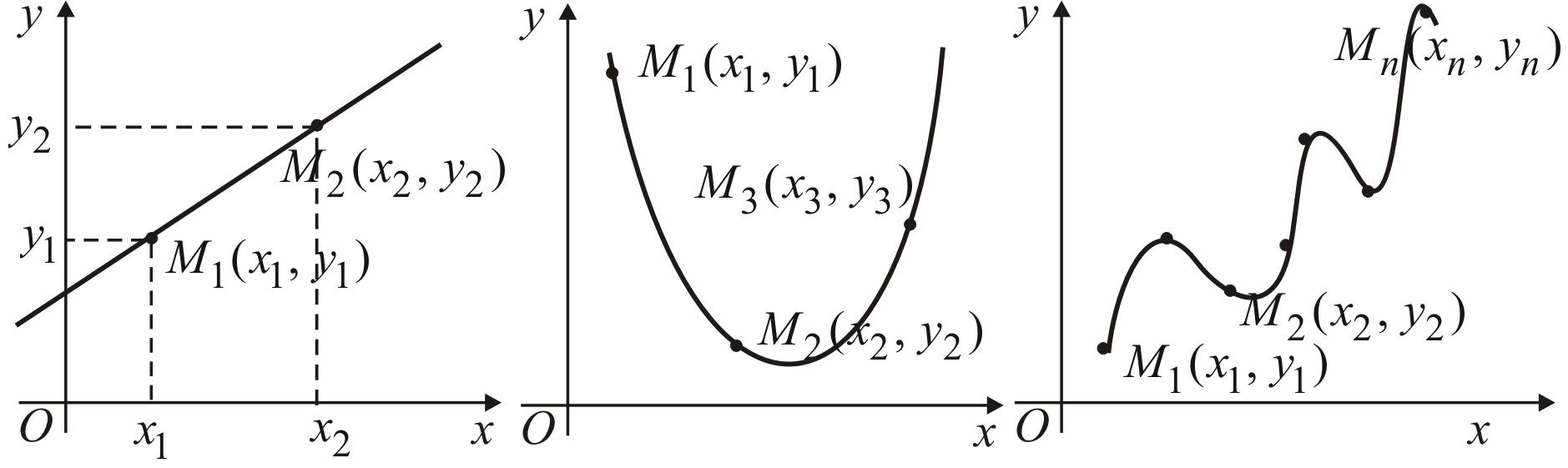
Рис. 50
В случае, если
имеются два точки
![]() ,
,
![]() ,
то данная формула позволяет написать
уравнение прямой, проходящей через эти
точки
,
то данная формула позволяет написать
уравнение прямой, проходящей через эти
точки
 .
.
В случае, если
имеются три точки
![]() ,
,
![]() ,
,
![]() ,
то данная формула позволяет написать
уравнение параболы, проходящей через
эти точки
,
то данная формула позволяет написать
уравнение параболы, проходящей через
эти точки
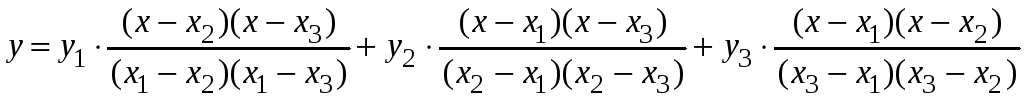 .
.
Если известно n точек, то можно написать уравнение линии, представляющей многочлен (n1)-ой степени относительно х.
Пример 3.25.
Написать уравнение параболы, проходящей
через точки
![]() .
.
В соответствии с многочленом Лагранжа записываем
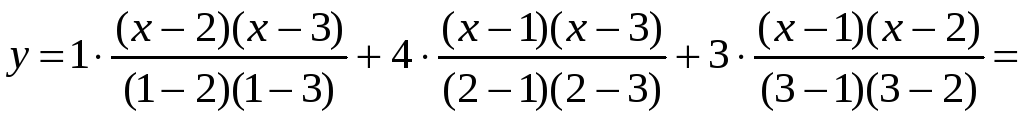
![]()
![]() ,
т. е.
,
т. е.
![]() .
.
Интерполяционный многочлен Лагранжа позволяет записать уравнение кривой, проходящей через любое число заданных точек. Однако, его удобно использовать при небольшом числе точек. В экономических задачах число точек может быть равным сотням и тысячам. Использование многочленов очень высокого порядка представляет затруднение даже при использовании современных вычислительных устройств. Поэтому при решении экономических задач используют методы аппроксимации.
Аппроксимацией называется нахождение функции заданного вида, обеспечивающей наилучшее приближение к опытным данным.
В методе наименьших
квадратов (МНК) качество приближения
оценивается по сумме квадратов отклонений
значений аппроксимирующей функции
![]() от опытных данных
от опытных данных
![]() i
= 1, 2, … (рис.
51), т. е.
i
= 1, 2, … (рис.
51), т. е.
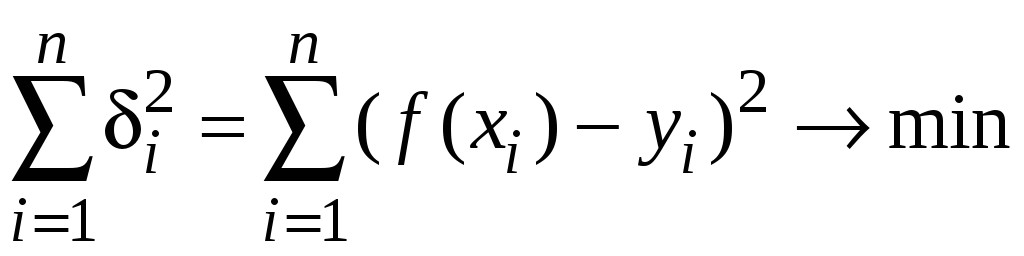 .
.
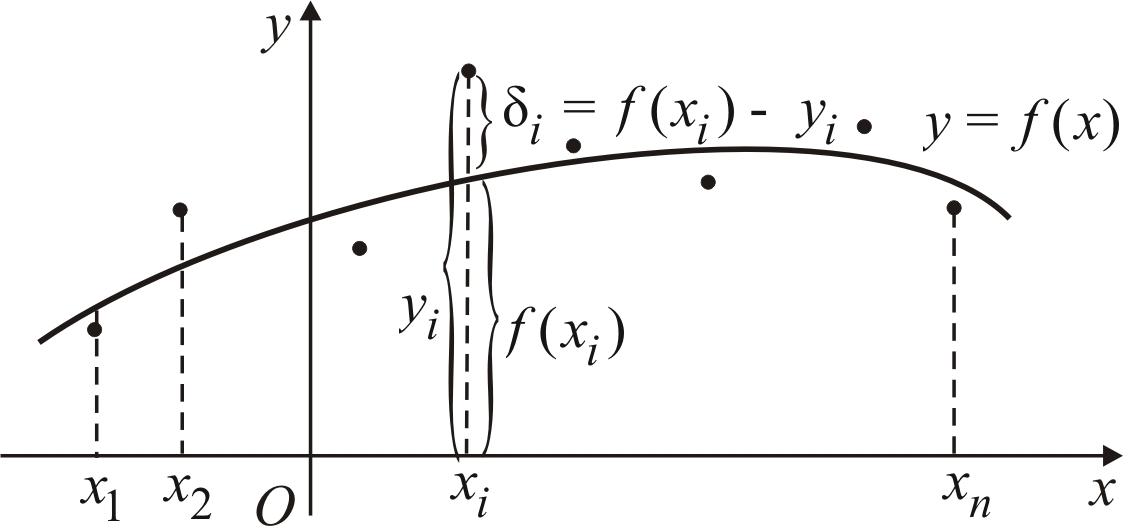
Рис. 51
Функция, по которой оценивается качество аппроксимации, называется критерием качества.
Аппроксимирующую
функцию выбирают в зависимости от
характера расположения точек опытных
данных. Эта функция
![]() обычно
имеет несколько неизвестных параметров
обычно
имеет несколько неизвестных параметров
![]() .
Для нахождения этих параметров составляют
критерий качества аппроксимации.
.
Для нахождения этих параметров составляют
критерий качества аппроксимации.
В методе наименьших квадратов критерий качества примет вид
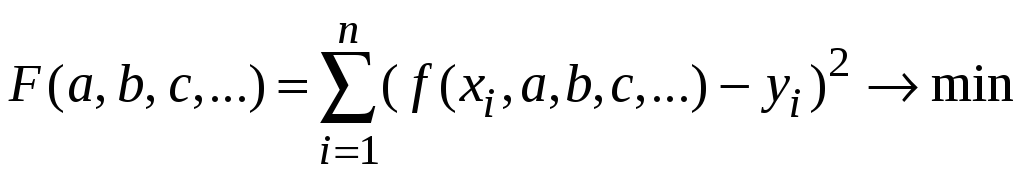 .
.
Для нахождения
неизвестных параметров a,
b,
c,
…, обеспечивающих минимальное значение
критерию качества, используют необходимый
признак экстремума функции нескольких
переменных. Согласно данному признаку
в точках экстремума функции нескольких
переменных все частные производные
либо равны нулю, либо не существуют.
Функция
![]() данного вида является дифференцируемой,
поэтому при оптимальных значениях
параметров a,
b,
c,
… все частные производные критерия
качества должны равняться нулю, т. е.
данного вида является дифференцируемой,
поэтому при оптимальных значениях
параметров a,
b,
c,
… все частные производные критерия
качества должны равняться нулю, т. е.
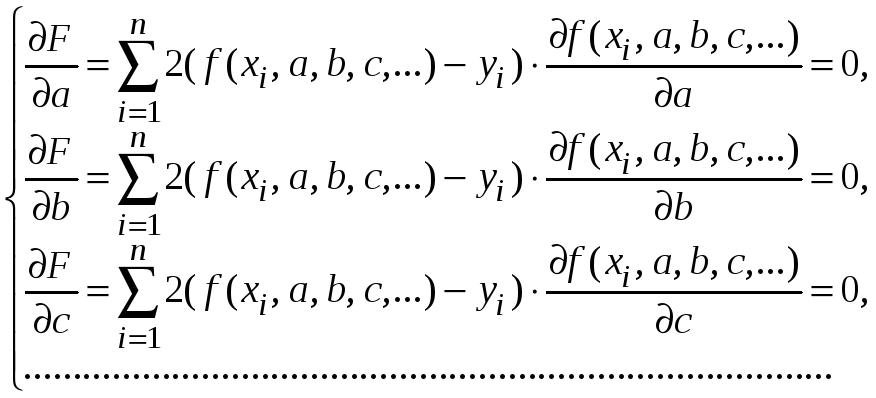
В качестве
аппроксимирующих функций часто используют
функции следующего вида: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
Составим системы уравнений для нахождения параметров аппроксимирующих функций.
-
В случае, когда
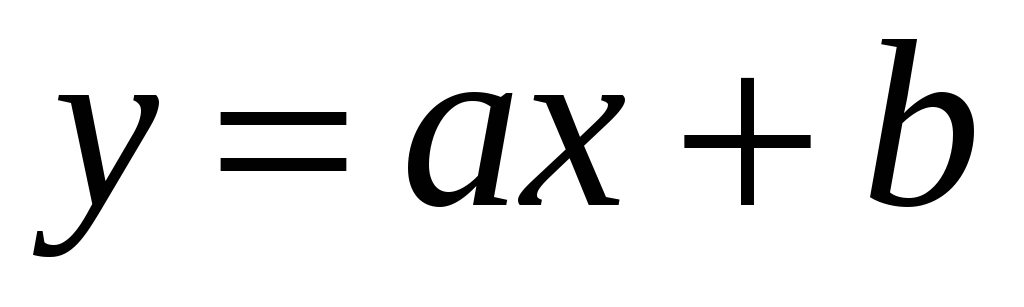 критерий качества имеет вид
критерий качества имеет вид
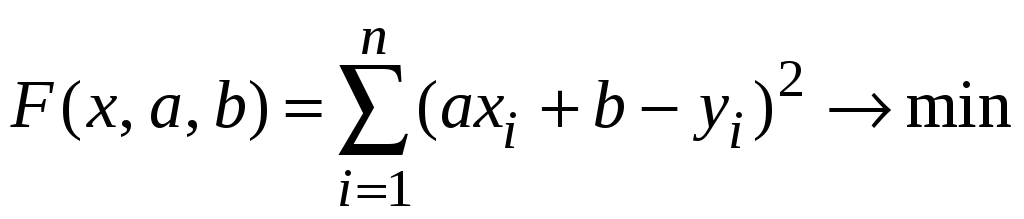 .
.
Найдем частные производные этой функции, получим систему для нахождения a, b.
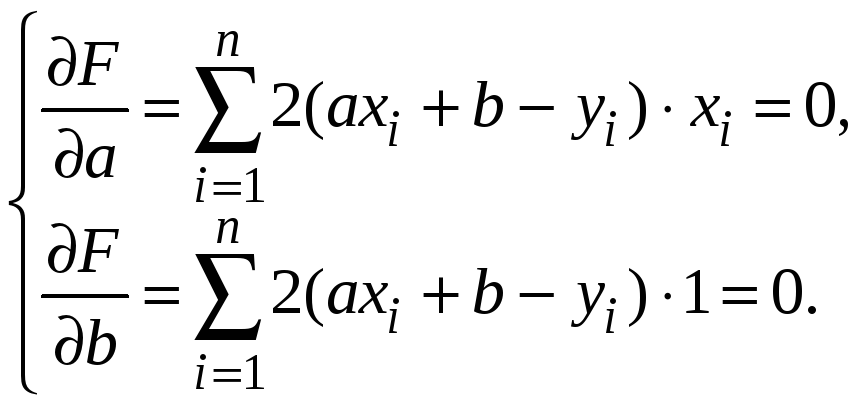

-
В случае, когда
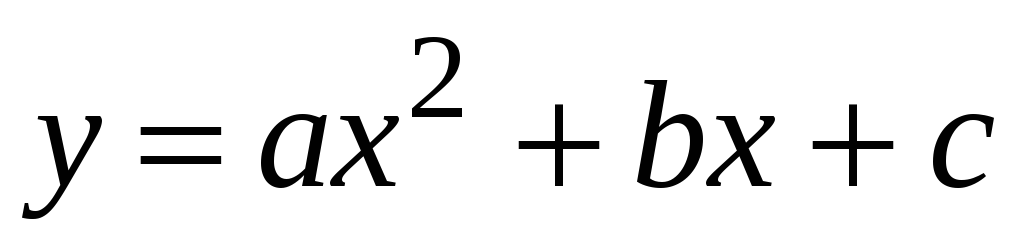 критерий качества имеет вид
критерий качества имеет вид
 .
.
Найдем частные производные этой функции, получим систему для нахождения коэффициентов a, b, с.
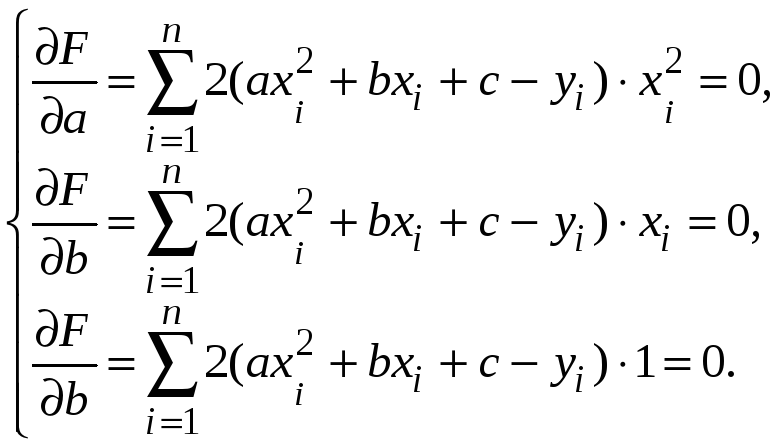
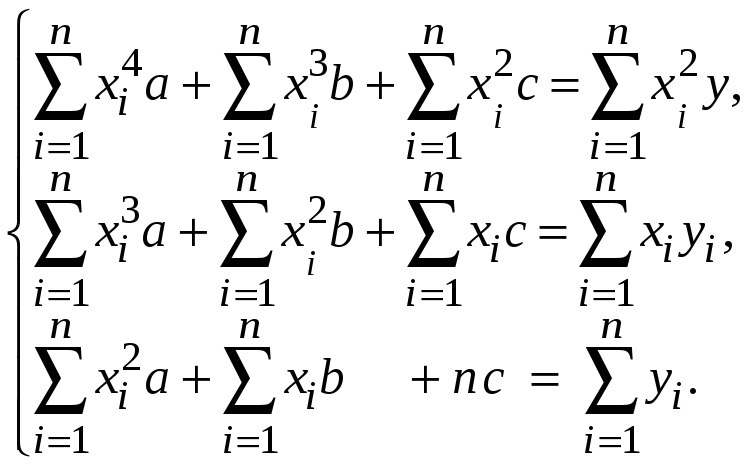
3. В случае, когда
аппроксимирующая функция имеет вид
![]() ,
необходимо сначала прологарифмировать
эту функцию
,
необходимо сначала прологарифмировать
эту функцию
![]() .
Тогда критерий качества
.
Тогда критерий качества
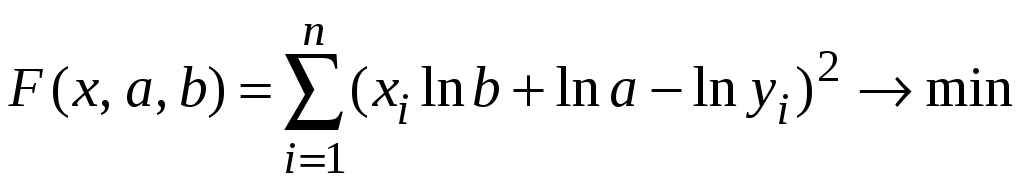 .
.
Система для нахождения lna и lnb имеет вид
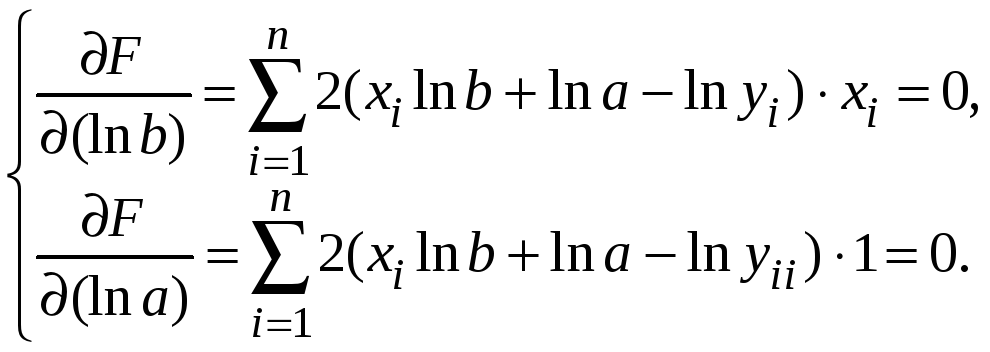
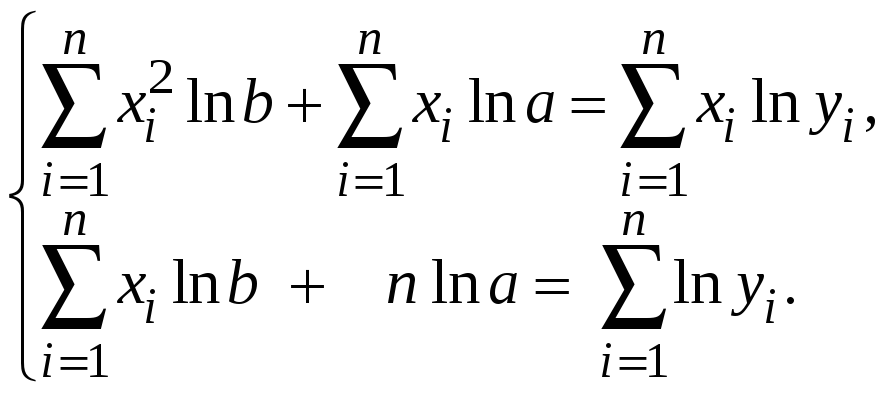
После того, как будут найдены логарифмы lna и lnb нужно найти a и b.
Пример 3.26. Заапроксимировать опытные данные
|
|
2 |
1 |
0 |
1 |
2 |
|
|
5 |
3 |
1 |
4 |
6 |
многочленом второй
степени
![]() .
На рисунке изобразить опытные данные
(«жирными точками») и график аппроксимирующей
функции. Вычислить значение критерия
качества.
.
На рисунке изобразить опытные данные
(«жирными точками») и график аппроксимирующей
функции. Вычислить значение критерия
качества.
Вычисления коэффициентов системы для нахождения коэффициентов a, b, c приведены в таблице.
|
i |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
5 |
4 |
8 |
16 |
10 |
20 |
5,06 |
0,06 |
0,0036 |
|
2 |
1 |
3 |
1 |
1 |
1 |
3 |
3 |
2,57 |
0,43 |
0,1849 |
|
3 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1,94 |
0,94 |
0,8836 |
|
4 |
1 |
4 |
1 |
1 |
1 |
4 |
4 |
3,17 |
0,83 |
0,6889 |
|
5 |
2 |
6 |
4 |
8 |
16 |
12 |
24 |
6,86 |
0,86 |
0,7396 |
|
|
0 |
19 |
10 |
0 |
34 |
3 |
51 |
|
|
2,5006 |
Составляем систему для нахождения коэффициентов a, b, c и решаем ее.

Аппроксимирующая
функция
![]() .
.
|
Рис. 52 |
Опытные данные в виде точек и график аппроксимирующей функции приведены на рис. 52.
|