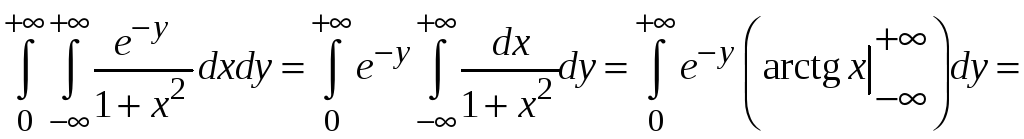
.

Пример 5.24. Найти интеграл .

.

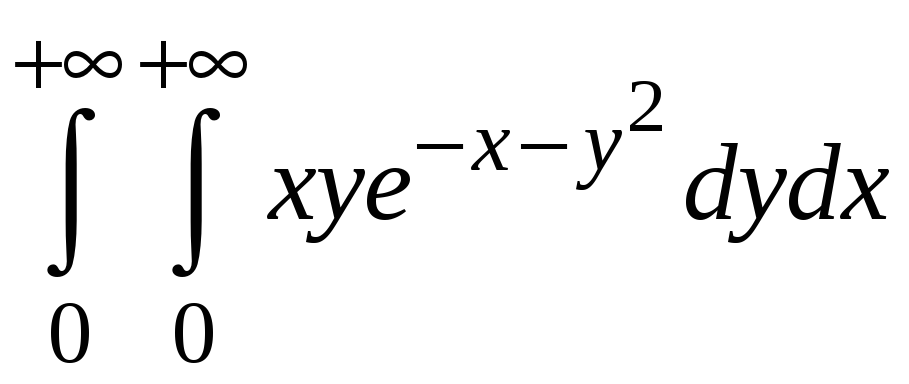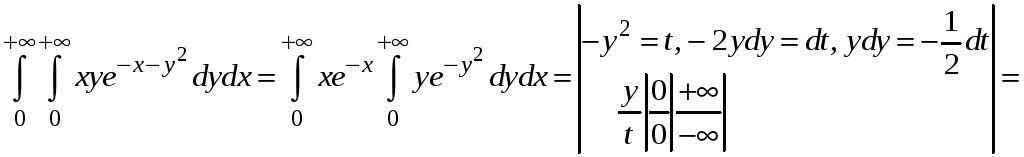
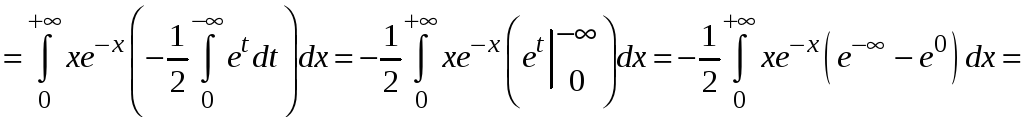
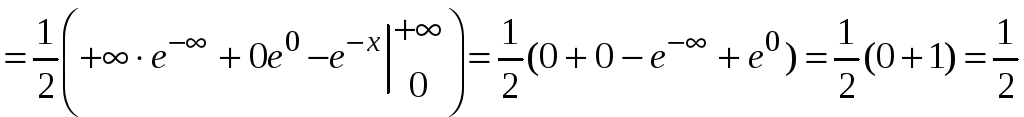Глава 7. Дифференциальные уравнения

7.1. Общие понятия

Уравнение называется дифференциальным, если оно содержит производные или дифференциалы искомой функции, искомую функцию и независимую переменную.

В общем случае дифференциальное уравнение имеет вид:

или .

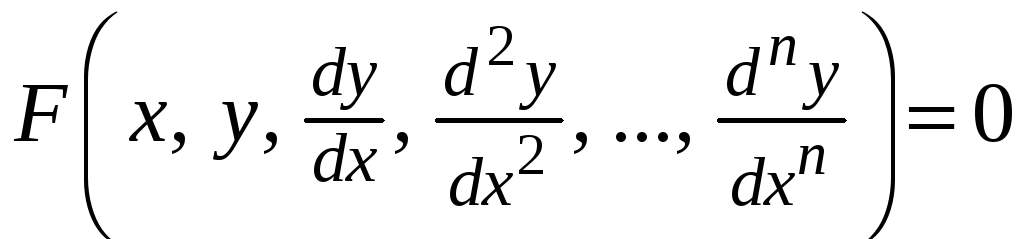Порядком дифференциального уравнения называется наивысший порядок производных искомой функции, входящей в уравнение.

Например:

уравнения первого порядка;

уравнение второго порядка;

уравнение третьего порядка.

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одной переменной. Приведенные выше дифференциальные уравнения обыкновенные.

Дифференциальное уравнение называется уравнением в частных производных, если искомая функция зависит от нескольких переменных.

Например, .

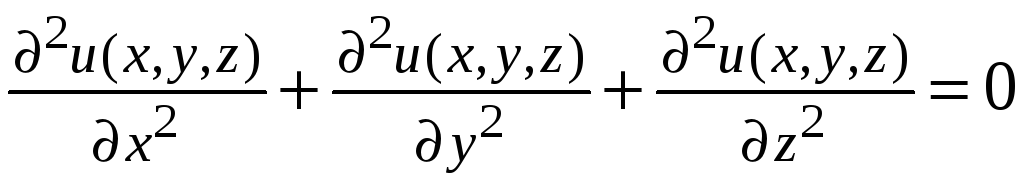Дифференциальное уравнение называется линейным, если оно линейное относительно искомой функции и ее производных, т. е. функция и ее производные входят в уравнение только в первой степени.

В общем случае линейное дифференциальное уравнение имеет вид

,

где  непрерывные функции.

Если в этом уравнении правая часть равна нулю, то уравнение называется однородным, иначе неоднородным.

Например,  линейное однородное уравнение,  линейное неоднородное уравнение.

Дифференциальное уравнение называется нелинейным, если оно является нелинейным относительно искомой функции или ее производных.

Например, нелинейными являются уравнения: , , .

Решением дифференциального уравнения называется любая функция, которая при подстановке в уравнение обращает его в тождество.

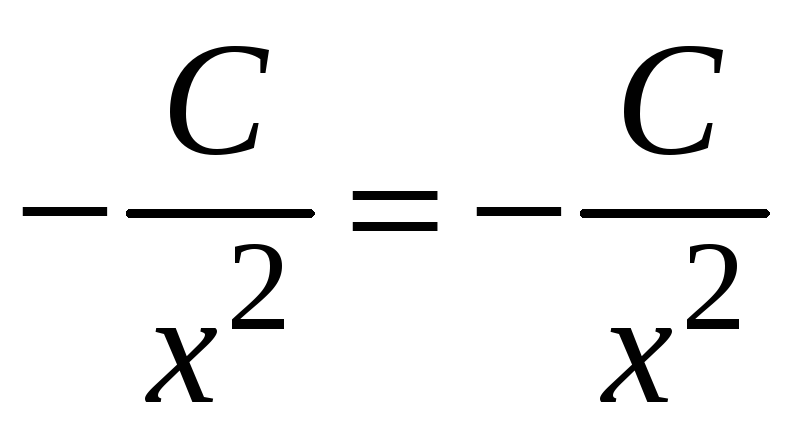
Пример 7.1. Проверить является ли функция решением уравнения . Находим . Подставляем и в уравнение, получаем   тождество. Следовательно, данная функция является решением уравнения.

Пример 7.2. Проверить являются ли решениями дифференциального уравнения функции .

Находим , подставляем в уравнение , получаем тождество .

Находим производные второй функции

, , подставляем их в уравнение, получаем

также тождество.

Следовательно, обе функции являются решениями одного и того же уравнения.

Решить дифференциальное уравнение – значит найти все его решения.

Решим два простых уравнения: и .

Находим .

Следовательно, решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.

Решим второе уравнение.

.

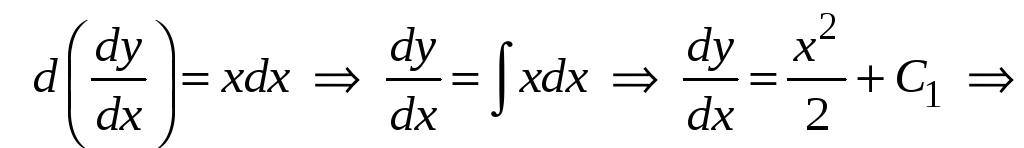
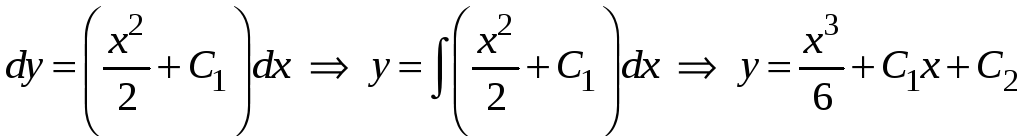Следовательно, дифференциальное уравнение второго порядка содержит две произвольные постоянные. Из данных примеров можно заметить, что решение дифференциального уравнения содержит столько произвольных постоянных, каков порядок уравнения.

Общим решением дифференциального уравнения n-го порядка называется решение данного уравнения, содержащее столько произвольных постоянных, независящих друг от друга, каков порядок уравнения, т. е. n.

Часто общее решение дифференциального уравнения невозможно найти в явном виде, а можно получить его только в неявной записи. Поэтому вводится понятие общего интеграла

Общим интегралом дифференциального уравнения n-ого порядка называется уравнение, получающееся при интегрировании дифференциального уравнения, не содержащее производных и дифференциалов искомой функции, а содержащее n произвольных постоянных, независящих друг от друга.

Таким образом, общее решение дифференциального уравнения n-ого порядка имеет вид

,

а общий интеграл

.

Частным решением (интегралом) дифференциального уравнения называется решение (интеграл), получающийся из общего при конкретных значениях произвольных постоянных.

График частного решения дифференциального уравнения называется интегральной кривой.

Общее решение дифференциального уравнения представляет семейство интегральных кривых.

Если известно общее решение или общий интеграл, то можно найти соответствующее им дифференциальное уравнение.

Пусть имеется общее решение . Для составления соответствующего ему дифференциального уравнения необходимо найти столько производных данного решения, сколько произвольных постоянных оно содержит. Тогда получится система, состоящая из (n+1)-го уравнения с n произвольными постоянными .

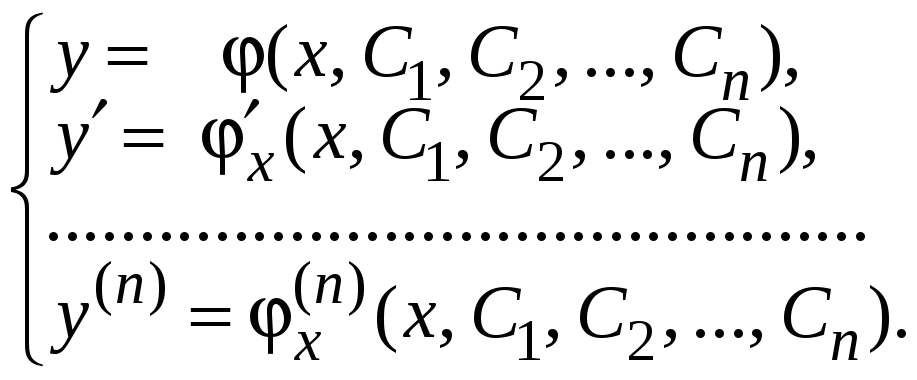
Для того чтобы получить соответствующее дифференциальное уравнение, необходимо в этой системе исключить произвольные постоянные. Например, найти из первых n соотношений и подставить в последнее.

Пример 7.3. Найти дифференциальное уравнение, для которого общее решение имеет вид .

Находим .

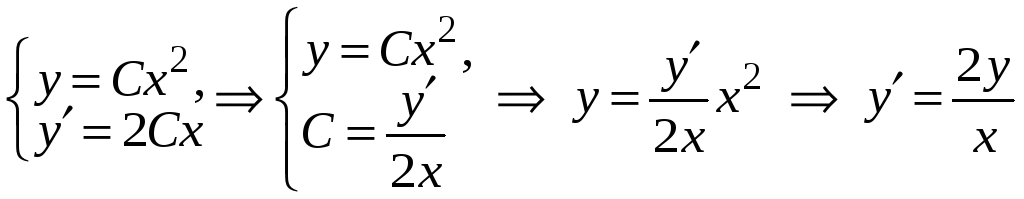Пример 7.4. Найти вид дифференциального уравнения, если общее решение .

Составляем систему

Из последнего соотношения имеем и подставляем в первое соотношение, получаем уравнение или .