Глава II. Дифференциальное исчисление функций одной переменной

2.1. Производная функции

2.1.1. Определение производной функции

Пусть функция непрерывна на отрезке и точка является внутренней точкой этого отрезка.

Определение. Производной функции в точке называется предел отношения приращения функции к приращению независимой переменной при , если этот предел существует (конечный или бесконечный), т. е.

.

Если , то говорят, что функция имеет бесконечно большую производную.

Если существуют только односторонние пределы при , то функция имеет односторонние производные .

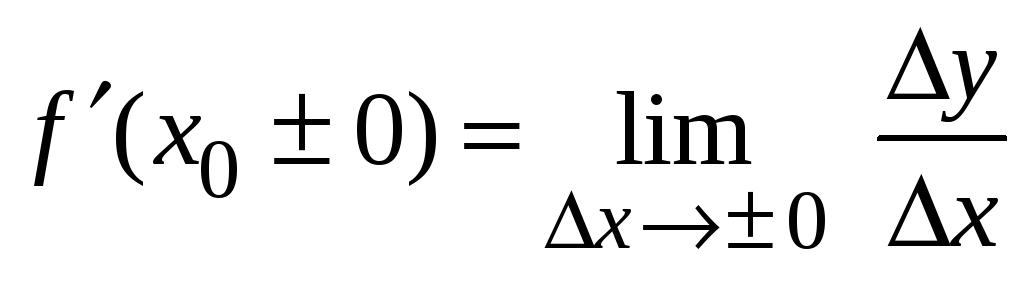Если функция имеет производные в любой точке интервала , то называется производной функции на этом интервале.

2.1.2. Дифференцируемость функции, ее взаимосвязь с производной и непрерывностью функции

Определение. Функция называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде , где , при .

Если функция дифференцируемая в точке , то она имеет конечную производную в этой точке. Действительно,

.

Справедливо также обратное утверждение, если функция одной переменной имеет конечную производную, то она дифференцируемая. Пусть , где . По теореме 1.3 о представлении функции в виде суммы предела и бесконечно малой функции

.

Следовательно, является дифференцируемой функцией.

Рассмотрим, как связана дифференцируемость функции с ее непрерывностью.

Если функция, дифференцируемая в точке, то она непрерывна в этой точке. Действительно, , что соответствует определению 1 непрерывности функции в точке.

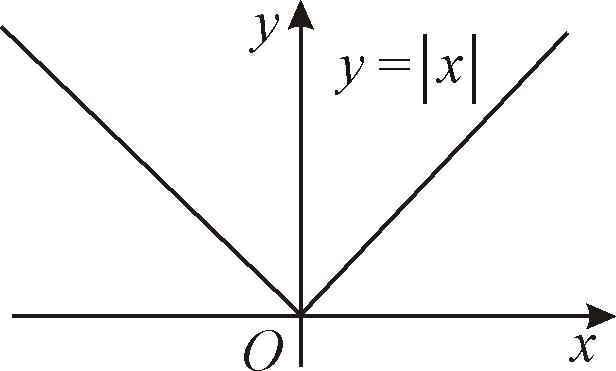
Однако, не всякая непрерывная функция является дифференцируемой.

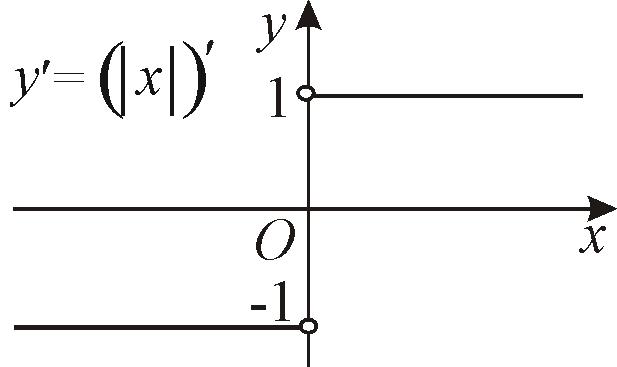
Например, функция является непрерывной в точке x = 0 (рис. 16) , а ее производная в точке x = 0 не существует (рис. 17). Следовательно, является не дифференцируемой в точке х = 0.

Рис. 16

Рис. 17

2.1.3. Непосредственное нахождение производной

Найти производные функций, используя определение производной.

1. . Производная постоянной равна нулю.

2. .

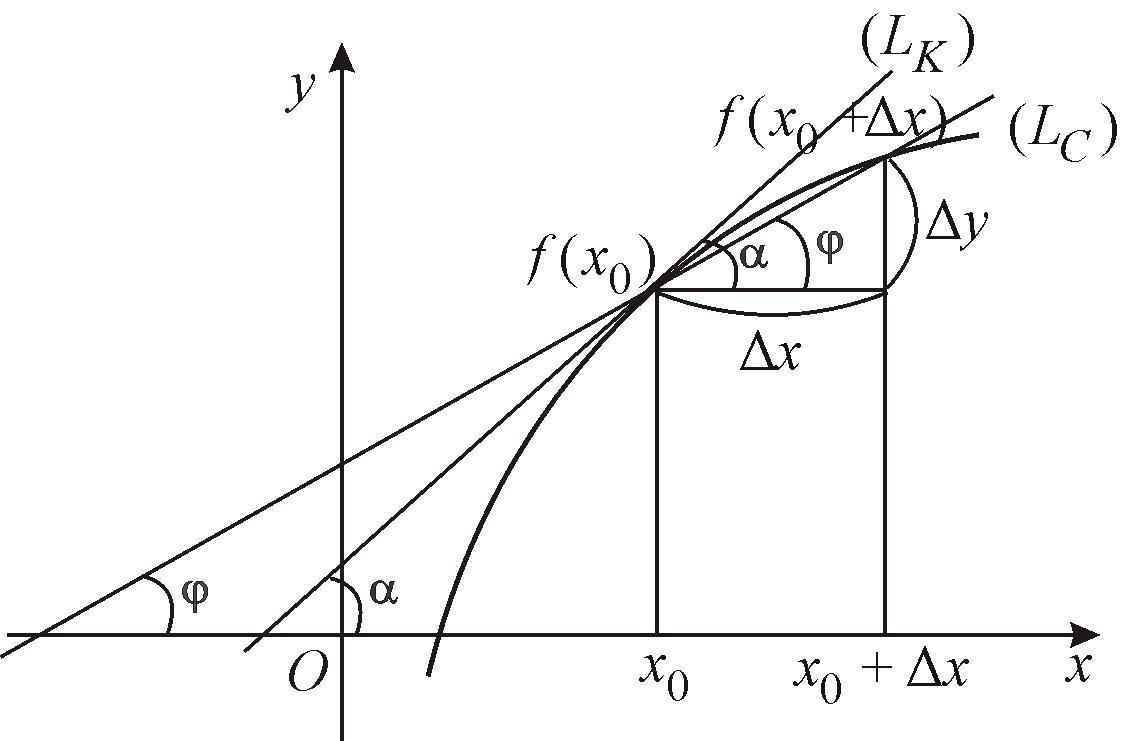
2.1.4. Геометрический смысл производной

Рис. 18

, где φ – угол наклона секущей , проходящей через точку к оси Оx. При секущая стремится к касательной и , где  – угол наклона к оси Ох касательной.

Таким образом, производная функции в точке равна тангенсу угла наклона касательной к графику этой функции в данной точке (рис. 18).

Используем этот факт, запишем уравнение касательной в точке

.

2.1.5. Механический смысл производной

Пусть S = S(t) является функцией зависимости пути от времени. Тогда

.

Отсюда следует, что производная функции равняется мгновенной скорости изменения функции.

2.1.6. Правила дифференцирования функций

Пусть u = u(x) и v = v(х) – дифференцируемые функции. Получим формулы дифференцирования суммы, произведения и частного функций. При этом используем определение производной и свойства пределов.

1. Производная суммы (разности) функций.

.

2. Производная произведения функций.

.

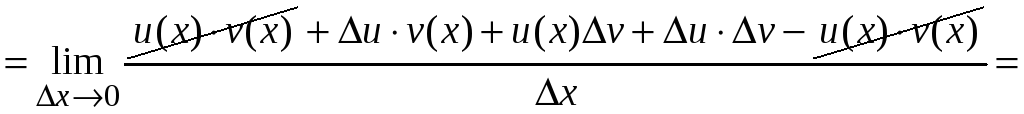
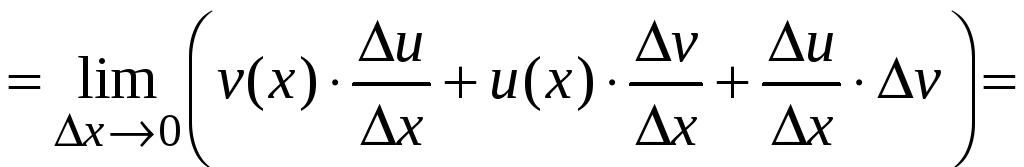
3. Производная частного функций (v(х)  0).

.

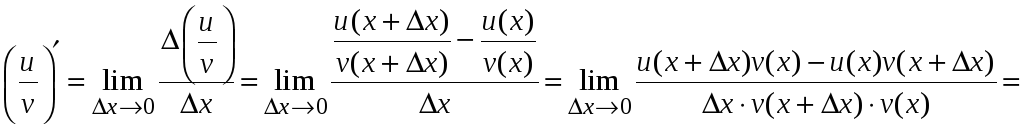
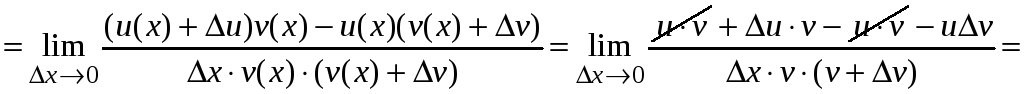
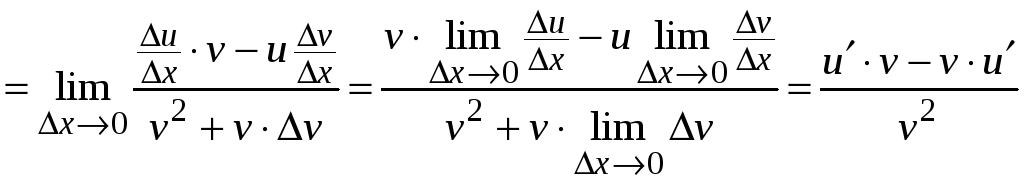4. Производная сложной функции , .

.

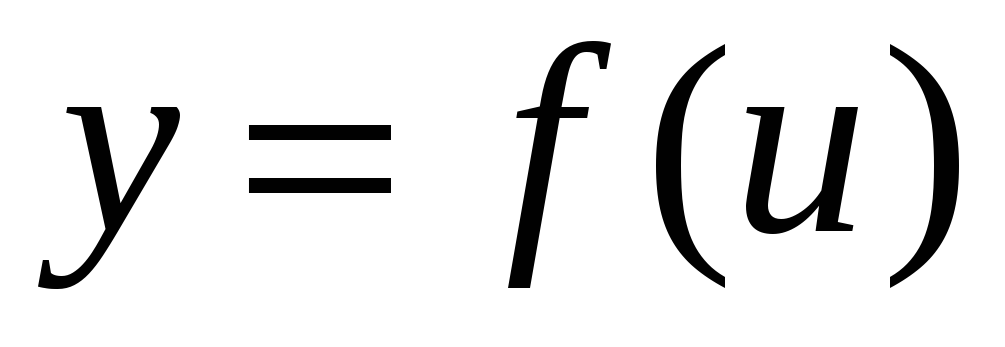Правило нахождения производной сложной функции. Производная сложной функции равняется произведению производных составляющих функций; причем при нахождении производных составляющих функций их аргументы не изменяются.

5. Производные взаимно обратных функци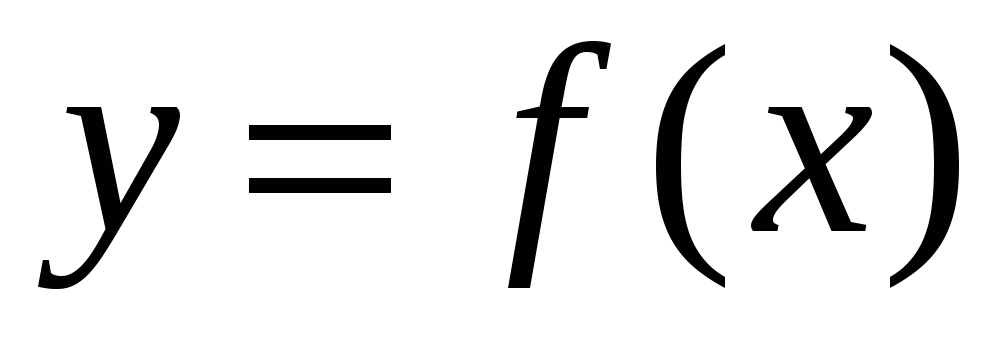й и .

.

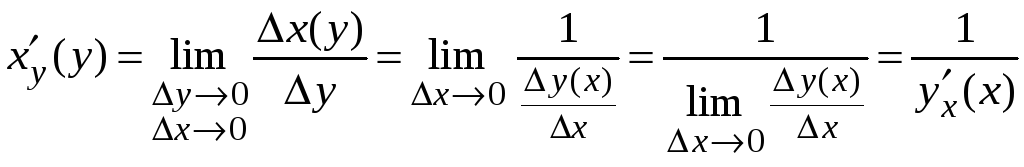Следовательно, производные взаимно обратных функций являются обратными по величине.