
- •§ 2. Свойства определителей 2-го и 3-го порядка.
- •§ 3. Миноры и алгебраические дополнения элементов матрицы 3-го порядка.
- •§ 4. Разложение определителя 3-го порядка по строке или столбцу.
- •§ 5. Определители 4-го порядка.
- •§ 6. Определители n-го порядка.
- •§ 1. Виды матриц, равенство матриц.
- •§ 2. Линейные действия с матрицами и их свойства.
- •§ 3. Умножение матриц и его свойства.
- •§ 4. Обратная матрица и ее свойства.
- •§ 5. Ранг матрицы.
- •§ 1. Основные понятия.
- •§ 2. Решение систем линейных уравнений по формулам Крамера.
- •§ 3. Решение систем линейных уравнений матричным способом.
- •§ 4. Исследование систем линейных уравнений.
- •§ 5. Решение систем линейных уравнений методом Гаусса.
- •§ 6. Однородные системы линейных уравнений.
- •Тема 1. О п р е д е л и т е л и
- •Тема 2. М а т р и ц ы
- •Тема 3. С и с т е м ы л и н е й н ы х у р а в н е н и й
- •§ 2. Линейные действия с векторами и их свойства.
- •§ 3. Линейные векторные пространства. Понятие базиса.
- •§ 4. Разложение вектора по базису.
- •§ 1. Проекция вектора на ось и ее свойства.
- •§ 2. Скалярное произведение векторов и его свойства.
- •§ 3. Векторное произведение векторов и его свойства.
- •§ 4. Смешанное произведение векторов и его свойства.
- •§ 1. Основные понятия.
- •§ 2. Линейные действия с векторами в ортонормированном базисе.
- •§ 3. Произведения векторов в координатах относительно ортонормированного базиса.
- •§ 4. Вычисление модуля, направляющих cos - ов и проекций векторов.
- •§ 1. Деление отрезка в данном отношении.
- •§ 2. Вычисление расстояния между двумя точками и угла между двумя векторами.
- •§ 3. Вычисление площадей и объемов.
- •Тема 1. Линейные действия с векторами
- •Тема 2. Умножение векторов
- •Тема 3. Прямоугольная декартова система координат
- •Тема 4. Геометрические задачи
§ 4. Разложение определителя 3-го порядка по строке или столбцу.
Определитель 3-го порядка равен сумме произведений элементов какой-нибудь строки (или столбца) на их алгебраические дополнения:
det
A =

det
A =

 +
+

 +
+
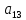
 - разложение по 1-й строке;
- разложение по 1-й строке;
det
A =

 +
+

 +
+

 - разложение по 2-й строке;
- разложение по 2-й строке;
det
A =

 +
+

 +
+

 - разложение по 3-й строке;
- разложение по 3-й строке;
det
A =

 +
+

 +
+

 - разложение по 1-му столбцу;
- разложение по 1-му столбцу;
det
A =

 +
+

 +
+

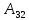 - разложение по 2-му столбцу;
- разложение по 2-му столбцу;
det
A =

 +
+

 +
+

 - разложение по 3-му столбцу.
- разложение по 3-му столбцу.
Пример.
Вычислить
определитель: det A
=

а) путем разложения по строке или столбцу;
б) с использованием его свойств.
разложение по 1-й строке: det A = 1(-4) + 2(-8) + 3(-10) = -4 -16 -30 = -50;
разложение по 3-му столбцу: det A = 3(-10) + 4(-5) + 0(-5) = -30 -20 + 0 = -50.
с использованием его свойств:
det
A =
 =
=
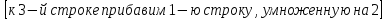 =
=
=
 =
=
 = 1
= 1 + 0 + 0 = - 50
+ 0 + 0 = - 50
§ 5. Определители 4-го порядка.
A
=
 - матрица 4 -го порядка;
- матрица 4 -го порядка;
 - элементы матрицы (i
= 1, … , 4; j = 1, … ,4).
- элементы матрицы (i
= 1, … , 4; j = 1, … ,4).
Mij
- минор элемента
 - это определитель матрицы 3 -го
порядка, полученной из данной матрицы
4 -го порядка путем вычеркивания
i -той строки и j
- того столбца:
- это определитель матрицы 3 -го
порядка, полученной из данной матрицы
4 -го порядка путем вычеркивания
i -той строки и j
- того столбца:
 M11
=
M11
=

 M23
=
M23
=

 M42
=
M42
=
 и т.д.
и т.д.
Aij
- алгебраическое дополнение
элемента
 :
:

A11 = M11 , A23 = - M23 , A42 = M42 , A34 = - M34 и т.д.
Правило
(выбора знака):

Пример.
A =

A11
=
 =
=
 = 2
= 2 + 0 − 3
+ 0 − 3 = −24 − 51 = −75
= −24 − 51 = −75
A23
= −
 =
=
 = − (0 − 1
= − (0 − 1 + 0) =
+ 0) =
 = 8 − 0 = 8
= 8 − 0 = 8
A34
= −
 =
=
 = −
= −
 =
=
=
 = −
= −
 =
=
=
 = − (0 − 0 + 1
= − (0 − 0 + 1 )
= −
)
= − = −24
= −24
Теорема. Сумма произведений элементов какой-нибудь строки (или столбца) на их алгебраические дополнения есть величина постоянная:

 +
+

 +
+

 +
+

 =
=

 +
+

 +
+

 +
+

 =
=
=

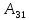 +
+

 +
+

 +
+

 =
=

 +
+

 +
+

 +
+

 =
=
=

 +
+

 +
+

 +
+

 =
=

 +
+

 +
+

 +
+

 =
=
=

 +
+

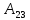 +
+

 +
+

 =
=

 +
+

 +
+

 +
+


Определитель 4-го порядка - это число, равное сумме произведений элементов какой-нибудь строки (или столбца) на их алгебраические дополнения:
det
A =
 =
=

 +
+

 +
+

 +
+

 , i = 1, 2, 3, 4
, i = 1, 2, 3, 4
или:
det
A =
 =
=

 +
+

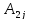 +
+

 +
+

 , j = 1, 2, 3, 4
, j = 1, 2, 3, 4
Свойства определителей 4-го порядка - такие же, как и для определителей 2-го и 3-го порядков (свойства 1÷9).
Вычисление определителей 4-го порядка намного упрощается, если разумно применить свойства определителей, например: получить много нулей в какой-нибудь строке или столбце или привести определитель к треугольному виду.
Пример.
det
A =
 =
=
 =
=
=
 =
=
 =
=
=
 =
=
 =0 + 0 + 0 + 1
=0 + 0 + 0 + 1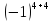
 =
=
=
 =
=
 =
=
=
 =
=
 =
=
=
 =
=
 = 0 + 1
= 0 + 1
 + 0 =
+ 0 =
= − = −(135 + 44) = −179.
= −(135 + 44) = −179.
§ 6. Определители n-го порядка.
A
=
 - матрица n -
го порядка,
- матрица n -
го порядка,
 - элементы матрицы (i
= 1, 2, …, n; j
= 1, 2, …, n).
- элементы матрицы (i
= 1, 2, …, n; j
= 1, 2, …, n).
Mij
- минор элемента
 - это определитель матрицы (n
- 1) - го порядка, полученной из данной
матрицы n - го
порядка путем вычеркивания i
-той строки и j - того
столбца.
- это определитель матрицы (n
- 1) - го порядка, полученной из данной
матрицы n - го
порядка путем вычеркивания i
-той строки и j - того
столбца.
Aij
- алгебраическое дополнение
элемента
 .
.

Теорема. Сумма произведений элементов какой-нибудь строки (или столбца) матрицы n - го порядка на их алгебраические дополнения есть величина постоянная:

 +
+

 + … +
+ … +

 =
=

 +
+

 +
+
 +
+

 , i = 1, 2, … , n,
j = 1, 2, …, n.
, i = 1, 2, … , n,
j = 1, 2, …, n.
Определитель n - го порядка - это число, равное сумме произведений элементов какой-нибудь строки (или столбца) матрицы n - го порядка на их алгебраические дополнения:
det
A =
 =
=

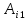 +
+

 + … +
+ … +

 =
=

 +
+

 +
+
 +
+
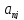
 ,
,
i = 1, 2, … , n, j = 1, 2, …, n.
Свойства определителей n-го порядка - такие же, как и для определителей 2-го, 3-го и 4-го порядков (свойства 1÷9).
Пример.
Вычислить определитель n
-го порядка: det A
=
 .
.
Ко всем строкам прибавим первую строку, умноженную на (-1):
det A
=
 .
.
Получили определитель треугольной матрицы, который по свойству (9) равен произведению элементов, стоящих на главной диагонали:
det A
= 1( )(
)( )
… (
)
… ( )
= (
)
= ( )(
)( )
… (
)
… ( ).
).
Пример.
Вычислить определитель n
-го порядка: det A
=
 .
.
(Элементы главной диагонали равны нулю, а все остальные элементы равны 1).
Все строки прибавим к первой строке:
det A
=

Из первой строки вынесем общий множитель:
det A
= ( )
)

Вычтем первую строку из всех остальных строк:
det
A = ( )
)
 =
=
 (
( ).
).
Задачи по теме 1.
. Вычислить определители 2-го порядка (довести до числового значения).
1.
 2.
2.
 3.
3.

4.
 5.
5.
 6.
6.

7.
 8.
8.
 9.
9.

10.
 11.
11.
 12.
12.

13.
 14.
14.
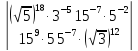
15.
 16.
16.

17.
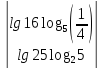 18.
18.

. Вычислить определители 3-го порядка:
− № 1 ÷ 8 - используя разложение по строке или столбцу;
− № 9 ÷ 16 - используя свойства определителей.
1.
 2.
2.
 3.
3.
 4.
4.

5.
 6.
6.
 7.
7.
 8.
8.

9.
 10.
10.
 11.
11.
 12.
12.

13.
 14.
14.
 15.
15.
 16.
16.

. Вычислить определители 4-го порядка.
1.
 2.
2.
 3.
3.

4.
 5.
5.
 6.
6.

7.
 8.
8.
 9.
9.

Дополнительные задачи.
1. Найти
многочлен: P(λ)
=
 и вычислить его корни.
и вычислить его корни.
2. Для
матрицы A =
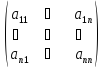 вычислить:
вычислить:
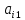
 +
+
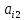
 + … +
+ … +

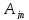 и
и

 +
+
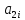
 +
+
 +
+
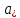
 ,
где i ≠ j
(
,
где i ≠ j
( - алгебраическое дополнение элемента
- алгебраическое дополнение элемента
 ).
).
Вычислить определители n -го порядка:
3.
 4.
4.
 5.
5.

6.
 7.
7.

 8.
8.
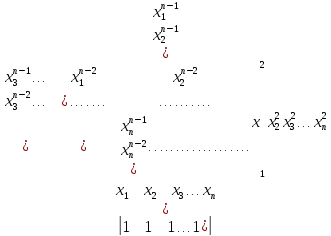 9.
9.

10.
 11.
11.
 = min
{i,j}
12.
= min
{i,j}
12.
 = max
{i,j}
= max
{i,j}
 2.
М А Т Р И Ц
Ы
2.
М А Т Р И Ц
Ы
