
- •Высшая математика
- •Вопросы для подготовки к комплексной контрольной работе по дисциплине «Высшая математика»
- •1. Матрицы. Действия с матрицами
- •2. Обратная матрица и ее вычисление
- •3. Определители и их свойства
- •4. Системы линейных алгебраических уравнений
- •5. Векторы. Скалярное, векторное, смешанное произведения векторов
- •6. Проекция вектора на ось
- •7. Прямая линия на плоскости
- •8. Прямая линия в пространстве
- •9. Уравнения плоскости
- •10. Кривые второго порядка
- •11. Предел числовой последовательности
- •12. Предел функции одной переменной в точке
- •13. Бесконечно большие и бесконечно малые функции
- •Свойства бесконечно малых и бесконечно больших функций
- •14. Замечательные пределы
- •15. Непрерывность функции в точке
- •16. Точки разрыва функции и их классификация
- •17. Производная функции. Правила дифференцирования функций
- •18. Правило Лопиталя для раскрытия неопределенностей
- •19. Исследование функций
- •20. Частные производные функции двух независимых переменных
- •23. Дифференциальные уравнения с разделяющимися переменными
- •24. Линейные дифференциальные уравнения первого порядка
- •25. Числовые ряды. Сходимость. Необходимый признак сходимости числового ряда
- •26. Достаточные признаки сходимости числовых рядов (признаки сравнения, Даламбера, Коши)
- •27. Знакочередующиеся ряды. Признак Лейбница
- •28. Степенные ряды. Радиус, интервал и область сходимости степенного ряда
- •2. Найти радиус сходимости, интервал сходимости степенного ряда
- •29. Определение вероятности события. Условная вероятность, сложение и умножение вероятностей Классическое определение вероятности
- •Сложение и умножение вероятностей
- •Формула полной вероятности. Формула Байеса
- •Испытания Бернулли
- •30. Математическое ожидание и дисперсия дискретных случайных величин
- •Минченков ю. В. Системы линейных алгебраических уравнений. Учебное пособие .– Мн.: чиУиП, 2004.- 36 с.
- •220086, Г. Минск, ул. Славинского, 1, корп. 3.
11. Предел числовой последовательности
1.![]() = (делим числитель
= (делим числитель
и
знаменатель на наивысшую степень п,
в данном случае на
![]() )
=
)
=
 .
.
2.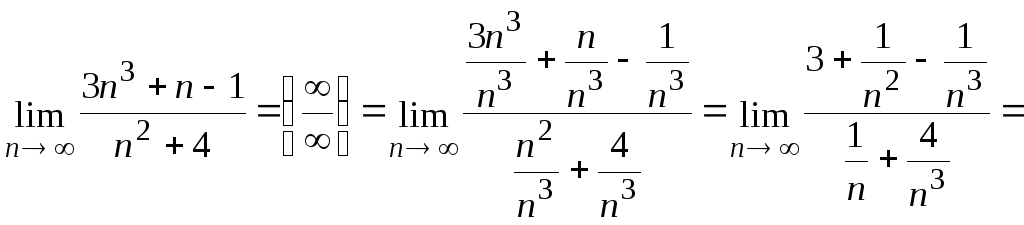
![]() .
.
3.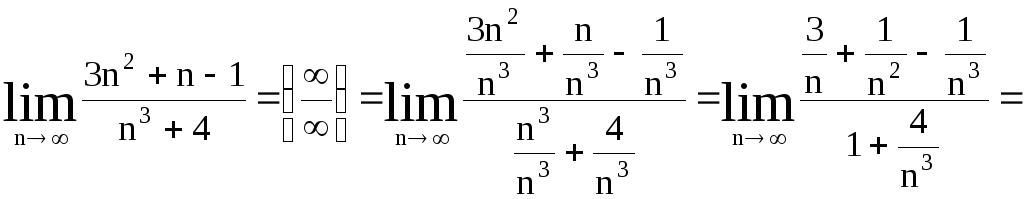
![]()
4.
При вычислении предела последовательности
часто возникает неопределенность
![]() .
В этом случае для ее раскрытия используют
следующий прием: выражение умножают и
делят на сопряженное выражение.
Проиллюстрируем это на примере:
.
В этом случае для ее раскрытия используют
следующий прием: выражение умножают и
делят на сопряженное выражение.
Проиллюстрируем это на примере:
![]()
![]()
![]() (делим
числитель и знаменатель на п)
(делим
числитель и знаменатель на п)
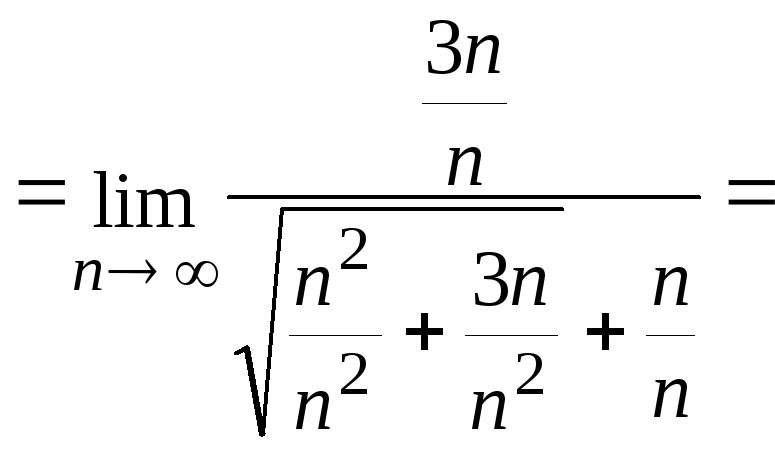
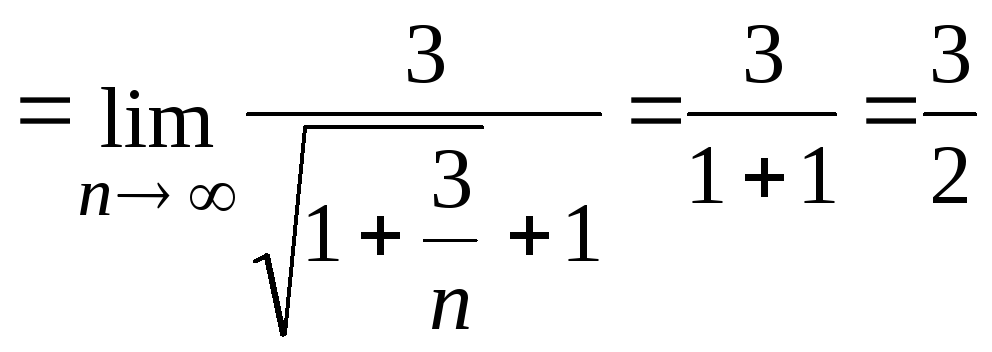 .
.
Задания для самостоятельной работы
1. Найти пределы:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() .
.
2. Найти пределы:
а)
![]() б)
б)
![]()
Ответы:
1. а)
![]() ,
б) 0, в) 2, г) 0.
,
б) 0, в) 2, г) 0.
2. а) 4, б) 1.
12. Предел функции одной переменной в точке
1. Найти предел функции.
а)
![]()
б)
![]()
2.
Найти односторонние пределы функции
![]() в точке
в точке
![]()
![]()
![]()
3. Нахождение предела функции в бесконечности алгоритмически совпадает с нахождением предела числовой последовательности.
а)
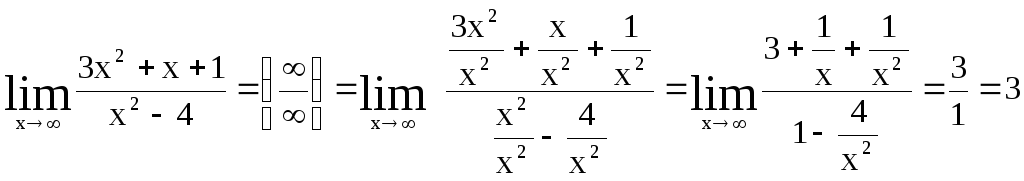 ;
;
б)
 ;
;
в)
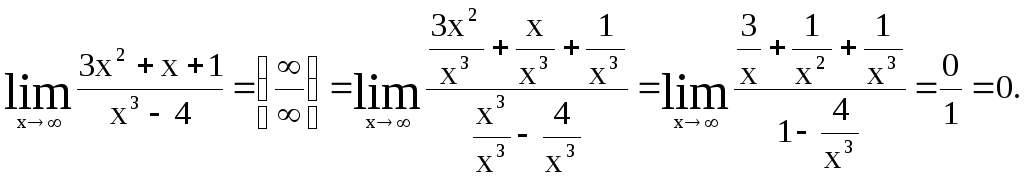
Задания для самостоятельной работы
-
Найти предел функции:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2. Найти предел функции:
![]() .
.
Ответы:
1.
а) 1, б)
![]() ,
в)
,
в)
![]() .
.
2. 1.
13. Бесконечно большие и бесконечно малые функции
Функция
![]() называется бесконечно
малой функцией
(б.м.ф.) при
называется бесконечно
малой функцией
(б.м.ф.) при
![]() ,
если
,
если

Функция
![]() называется бесконечно
большой функцией
(б.б.ф.) при
называется бесконечно
большой функцией
(б.б.ф.) при
![]() ,
если
,
если
 .
.
Пример.
а)![]() функция
функция![]() б.м.ф. при
б.м.ф. при
![]() .
.
б)![]() функция
функция![]() б.б.ф. при
б.б.ф. при
![]()
Свойства бесконечно малых и бесконечно больших функций
-
Сумма и произведение конечного числа б.м.ф при
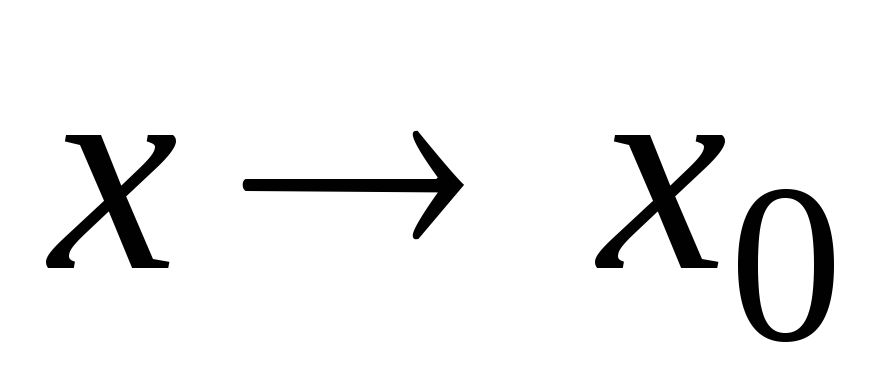 есть б.м.ф.
есть б.м.ф.
-
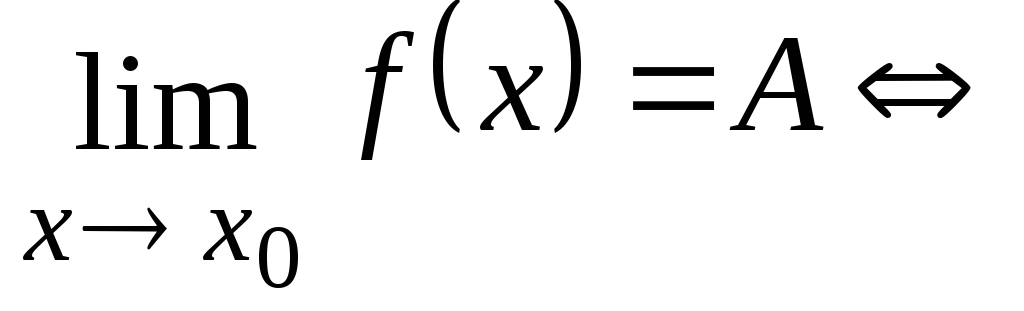 когда
когда
 где
где
 б.м.ф
при
б.м.ф
при
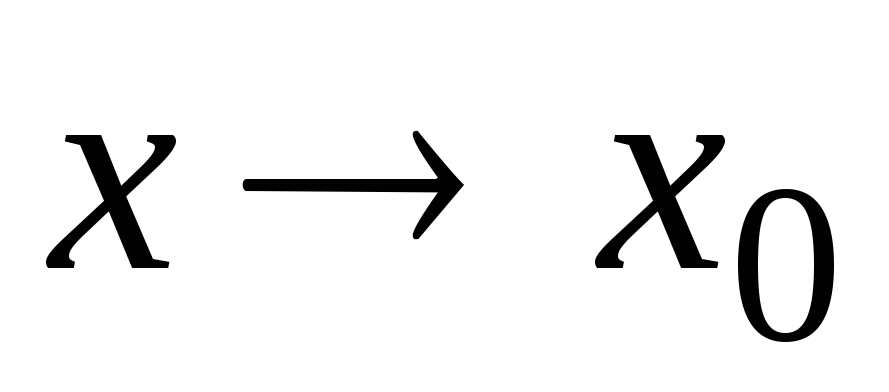 .
. -
Произведение двух б.б.ф при
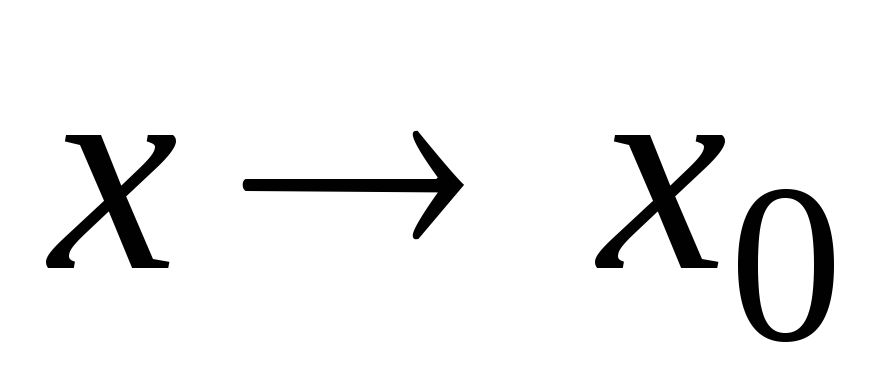 есть б.б.ф.
есть б.б.ф. -
Если
 б.б.ф при
б.б.ф при
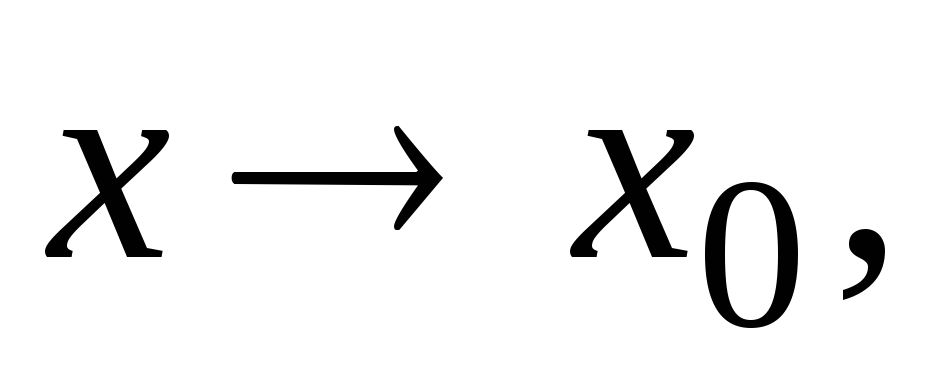 то
то
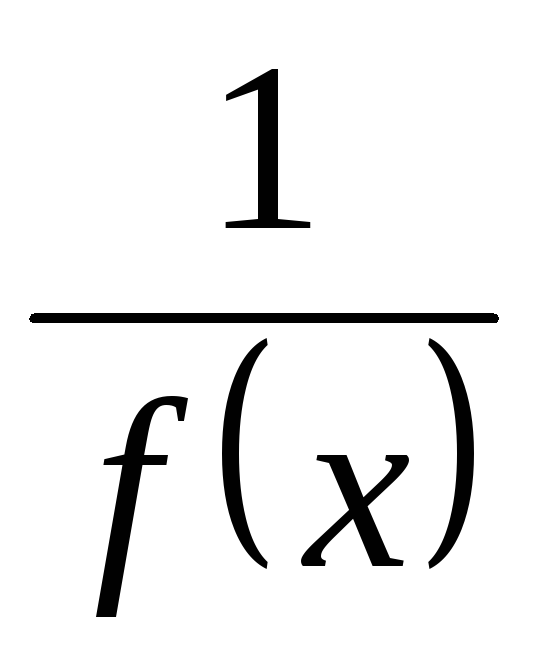 – б.м.ф. при
– б.м.ф. при
 .
Если
.
Если
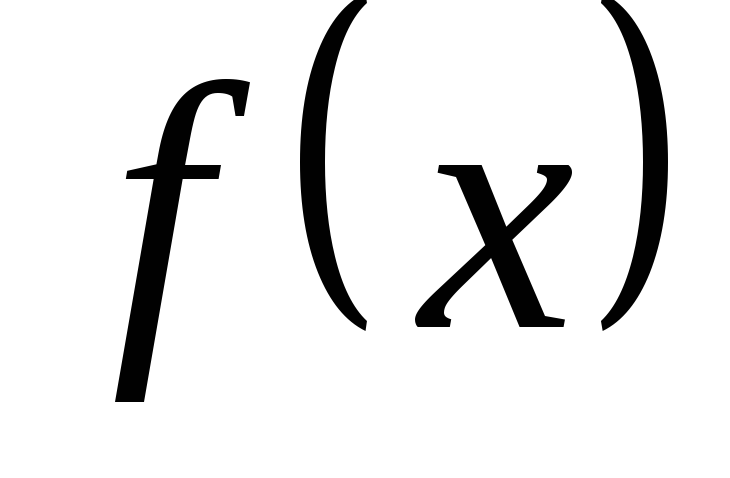 б.м.ф при
б.м.ф при
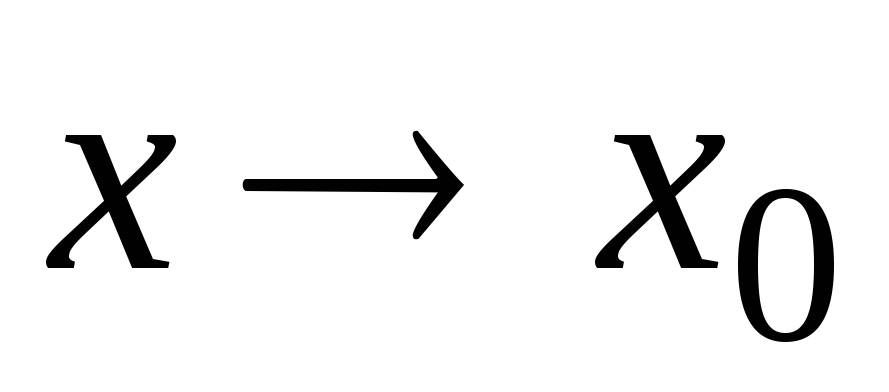 и
и
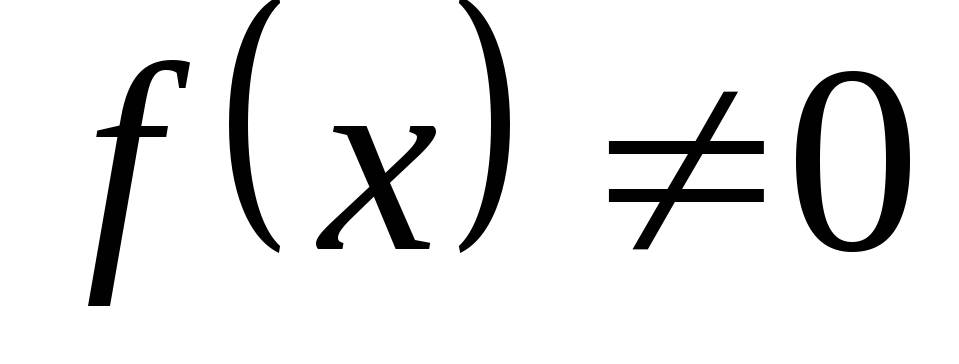 в некоторой окрестности точки
в некоторой окрестности точки
 то
то
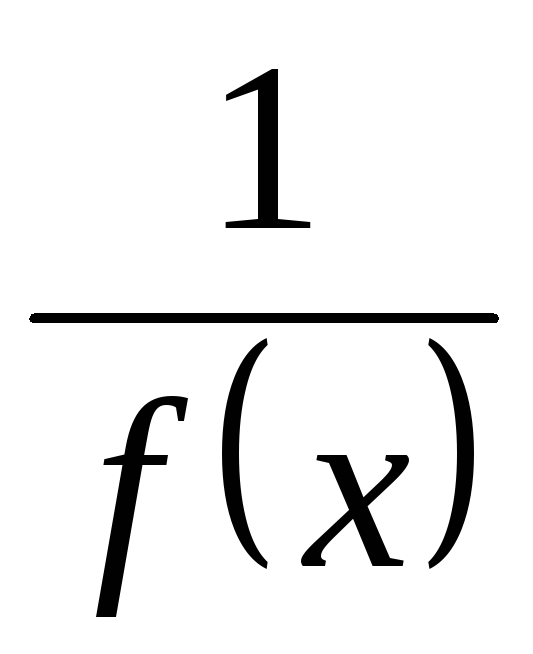 – б.б.ф при
– б.б.ф при
 (cм.
пример).
(cм.
пример).
14. Замечательные пределы
Первый замечательный предел:
![]() или
или
![]() .
Учитывая, что
.
Учитывая, что
![]() ,
имеем также, что
,
имеем также, что
![]() или
или
![]() .
.
Второй замечательный предел:
![]() или
или
![]() .
.
Рассмотрим на примерах использование замечательных пределов.
Пример
а)
![]() ,
т. к.
,
т. к.
![]() ;
;
б)
![]() ,
,
т. к.
![]()
![]()
в)
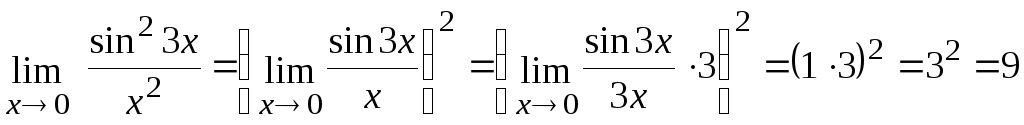 .
.
г)
![]() (Проверить самостоятельно);
(Проверить самостоятельно);
д)
![]() ,
т. к.
,
т. к.
![]() ;
;
е)
![]() ,
т. к.
,
т. к.
![]() ;
;
ж)
![]()
![]() ,
т. к.
,
т. к.![]() ,
,
![]() .
.
Задания для самостоятельной работы
Найти предел функции, используя первый и второй замечательные пределы.
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)
![]() е)
е)
![]() .
.
Ответы:
а)
![]() ,
б)
,
б)
![]() ,
в) 2, г)
,
в) 2, г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() .
.
15. Непрерывность функции в точке
Определение
1. Функция
![]() называется непрерывной в точке
называется непрерывной в точке
![]() ,
если выполнены следующие три условия:
1)
,
если выполнены следующие три условия:
1)
![]() определена
в точке
определена
в точке
![]() и ее окрестности; 2)
существует конечный предел функции
и ее окрестности; 2)
существует конечный предел функции
![]() в точке
в точке
![]() ;
3)
этот предел равен значению функции в
точке
;
3)
этот предел равен значению функции в
точке
![]() ,
т. е.
,
т. е.
![]() .
.
Определение
2. Функция
![]() называется непрерывной в точке
называется непрерывной в точке
![]() ,
если: 1)
,
если: 1)
![]() определена
в точке
определена
в точке
![]() и ее окрестности; 2)
бесконечно
малому приращению аргумента соответствует
бесконечно малое приращение функции:
и ее окрестности; 2)
бесконечно
малому приращению аргумента соответствует
бесконечно малое приращение функции:
![]()
Пример
1. Доказать,
что функция
![]() непрерывна в любой точке области
определения, т. е. в любой точке
непрерывна в любой точке области
определения, т. е. в любой точке
![]() .
.
Решение
Дадим
аргументу
![]() приращение
приращение
![]() в точке
в точке
![]() и найдем приращение функции
и найдем приращение функции
![]() :
:
![]()
![]() .
.
Следовательно,
![]()
![]()
![]() .
.
Таким
образом,
![]() ,
а это и означает, что функция
,
а это и означает, что функция
![]() непрерывна в точке
непрерывна в точке
![]() .
.
Пример
2. Исследовать
на непрерывность в точке
![]() следующие функции:
следующие функции:
а)
![]() ;
б)
;
б)
![]()
Решение
а)
Функция
![]() определена в окрестности точки
определена в окрестности точки
![]() ,
но в самой точке
,
но в самой точке
![]() она не определена, следовательно, в этой
точке она не является непрерывной (не
выполнено первое условие непрерывности).
она не определена, следовательно, в этой
точке она не является непрерывной (не
выполнено первое условие непрерывности).
б)
Для исследования на непрерывность
воспользуемся определением 2. В точке
![]() функция
функция
![]() определена (
определена (![]() ), т. е. первое условие непрерывности
выполнено; второе условие также
выполняется:
), т. е. первое условие непрерывности
выполнено; второе условие также
выполняется:
![]() ;
;
![]() ;
третье условие непрерывности не
выполняется, так как
;
третье условие непрерывности не
выполняется, так как
![]() .
Следовательно, данная функция также не
является непрерывной в точке
.
Следовательно, данная функция также не
является непрерывной в точке
![]() .
.
Задания для самостоятельной работы
Исследовать следующие функции на непрерывность в указанных точках:
а)
![]() б)
б)
![]() .
.
Ответы:
а)
![]() – точка разрыва второго рода;
– точка разрыва второго рода;
![]() – точка непрерывности функции;
– точка непрерывности функции;
б)
![]() – точка непрерывности функции;
– точка непрерывности функции;
![]() – точка разрыва второго рода.
– точка разрыва второго рода.
