
- •Теорія міри та інтеграла лебега
- •Глава I
- •1.1. Поняття множини, операції над множинами
- •Задачі.
- •1.2. Поняття відображення і взаємно однозначначної відповідності
- •Задачі.
- •3.1. Зчислені множини та їх властивості
- •Множини потужності континууму
- •Двійкові дроби.
- •Приклади важливих множин потужності континууму.
- •5.1 Існування потужності більшої, ніж с
- •Застосування теореми Бернштейна
- •Задачі.
- •Глава II
- •Властивості відкритих і замкнених множин
- •Глава III
- •3.1. Елементарні множини та їх властивості
- •. Міра елементарних множин та її властивість
- •3.3 Поняття зовнішньої міри обмеженої множини і її властивості.
- •3.4 Поняття вимірної множини
- •3.5 Поняття внутрішньої міри обмеженої множини.
- •Приклади вимірних множин і невимірної множини.
- •Приклад невимірної обмеженої множини.
- •3.6. Поняття півкільця, кільця, -алгебри
- •3.7. Поняття вимірної множини в
- •Узагальнення поняття вимірності в
- •3.8 Загальне поняття міри
- •Глава iy
- •Означення вимірної функції.
- •4.2.1 Приклади вимірних функцій
- •4.3.1. Загальні властивості вимірних функцій
- •4.4.1. Властивості вимірних функцій пов’язані з алгебраїчними операциями
- •4.5.1. Граничний перехід у класі вимірних функцій
- •Глава y
- •5.1. Означення інтеграла Лебега для простої функції і його властивості.
- •Приклади простих функцій інтегровних за Лебегом
- •Властивості інтеграла Лебега від простих функцій
- •5.2. Інтеграл Лебега і його властивості у загальному випадку.
- •Властивості інтеграла Лебега у загальному випадку
- •5.3. Граничний перехід під знаком інтеграла Лебега
- •5.4 Порівняння інтегралів Рімана і Лебега
- •5.5. Інтеграл Лебега по множені нескінченної міри
3.5 Поняття внутрішньої міри обмеженої множини.
Означення
3.5.1 Різниця
![]() називається внутрішньою мірою множини
називається внутрішньою мірою множини
![]() і позначається символом
і позначається символом
![]() .
.
Нехай![]() і
і![]() довільні
обмежені неперетинні множини і
довільні
обмежені неперетинні множини і
![]() .
Застосуємо нерівність (3.4.9) до множин
.
Застосуємо нерівність (3.4.9) до множин
![]()
![]() .
(3.4.14)
.
(3.4.14)
Використавши
рівність
![]() ,
віднімемо ліву і праву частини нерівністі
(3.4.14) від числа
,
віднімемо ліву і праву частини нерівністі
(3.4.14) від числа
![]() .
Тоді
.
Тоді
![]() (3.4.15)
(3.4.15)
На підставі означення 3.5.1 нерівність (3.4.15) можливо записати як
![]() ,
(3.4.16)
,
(3.4.16)
де
![]() і
і![]() довільні
обмежені неперетинні множини.
довільні
обмежені неперетинні множини.
По
індукції нерівність (3.4.16) поширюється
на випадок скінченної системи обмежених
неперетинних множин, а потім, внаслідок
монотонності внутрішньої міри і на
випадок зчисленної системи неперетинних
множин
![]() ,
об’єднання яких обмежене:
,
об’єднання яких обмежене:
![]() .
.
Оскільки
![]() довільне,
то маємо нерівність
довільне,
то маємо нерівність
![]() (3.4.17)
(3.4.17)
Теорема
3.5 Для
того щоб обмежена множина
![]() була вимірною, необхідно і достатньо
щоб
була вимірною, необхідно і достатньо
щоб
![]() .
(3.4.18)
.
(3.4.18)
Доведення.
Необхідність. Нехай множина
![]() є вимірною. Тоді вимірна множина
є вимірною. Тоді вимірна множина
![]() і
і
![]() .
Отже (3.4.18) виконується.
.
Отже (3.4.18) виконується.
Достатність.
Припустимо тепер, що (3.4.18) має місце.
Внаслідок властивості точної нижньої
межі для кожної з множин
![]() і
і
![]() та довільного числа
та довільного числа
![]() знайдеться скінченна, або зчисленна
система елементарних множин
знайдеться скінченна, або зчисленна
система елементарних множин
![]() така,
що
така,
що
![]()
![]() і
і
![]()
![]() .
Тоді на підставі наслідку 2 і внаслідок
того, що
.
Тоді на підставі наслідку 2 і внаслідок
того, що
![]()
![]()
![]()
![]() .
(3.4.19)
.
(3.4.19)
Якщо
множина![]() є об’єднання скінченної системи множин
є об’єднання скінченної системи множин
![]() ,
то в якості елементарної множини
,
то в якості елементарної множини
![]() візьмемо множину
візьмемо множину
![]() ,
а якщо нескінченної, то виберемо таке
,
а якщо нескінченної, то виберемо таке
![]() ,
що
,
що
![]() ,
і покладемо множину
,
і покладемо множину
![]() рівною
рівною
![]() .
Тоді
.
Тоді
![]() або порожня множина, або
або порожня множина, або
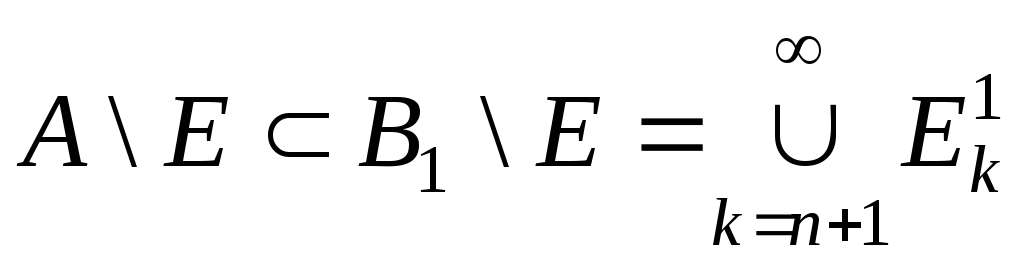 .
Отже
.
Отже
![]() ,
або
,
або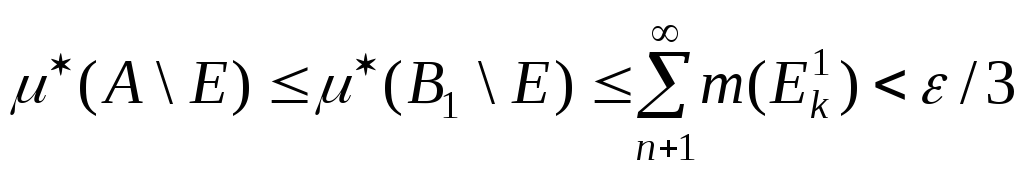 .
Розглянемо різницю
.
Розглянемо різницю
![]() .
Внаслідок нерівності (3.4.19)
.
Внаслідок нерівності (3.4.19)
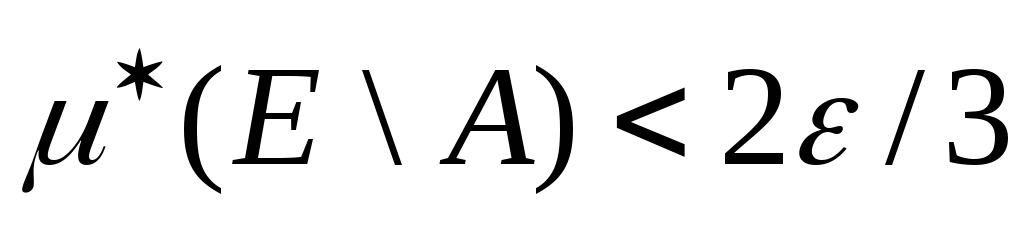 .
Отже
.
Отже
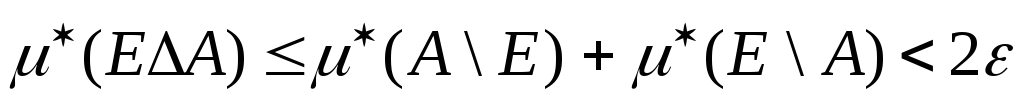 .
За означенням вимірної мнжини множина
.
За означенням вимірної мнжини множина
![]() є вимірною.
є вимірною.
Теорема доведена.
Приклади вимірних множин і невимірної множини.
1.
Будь-яка обмежена відкрита множина
![]() вимірна і
вимірна і
![]() дорівнює
сумі мір складових інтервалів.
дорівнює
сумі мір складових інтервалів.
Доведення.
Якщо
відкрита множина
![]() є об’єднання скінченної множини
складових інтервалів, то
є об’єднання скінченної множини
складових інтервалів, то
![]() елементарна
множина і
елементарна
множина і
![]() .
Нехай
.
Нехай
![]() .
Внаслідок властивості 10 множина
.
Внаслідок властивості 10 множина
![]() є вимірною і
є вимірною і
![]() .
.
2.
Будь-яка обмежена замкнена множина
![]() вимірна і
вимірна і
![]() ,
де
,
де
![]() найменший
сегмент, що містить замкнену множину
найменший
сегмент, що містить замкнену множину
![]() .
.
Доведення.
Нехай
![]() найменший
сегмент, що містить замкнену множину
найменший
сегмент, що містить замкнену множину
![]() .
Тоді множина
.
Тоді множина
![]() відкрита
і отже є вимірною, а тоді, внаслідок
властивості 1 вимірних множин,
відкрита
і отже є вимірною, а тоді, внаслідок
властивості 1 вимірних множин,
![]() вимірна і (завдяки наслідку із властивості
6)
вимірна і (завдяки наслідку із властивості
6)
![]() .
.
3.
Будь-яка обмежена не більш ніж зчисленна
множина A
вимірна і
![]()
Доведення.
В
силу адитивності,
якщо множина A
скінченна, або адитивності,
якщо множина A
зчисленна,
і тому що
міра
одно елементної множини дорівнює
нулю,
маємо
![]() .
.
4.
Означення 3.4.2 Необмежена
множина
![]() називається
вимірною, якщо до будь-якого
називається
вимірною, якщо до будь-якого
![]() вимірною є множина
вимірною є множина
![]() .
Мірою вимірної необмеженої множини
.
Мірою вимірної необмеженої множини
![]() називається
називається
![]() .
.
Так як
величина
![]() не спадає, коли
не спадає, коли
![]() зростає, то границя
зростає, то границя
![]() існує. Якщо вона дорівнює
існує. Якщо вона дорівнює
![]() ,
то
,
то
![]() .
.
Приклад.
Множини
![]() ,
будь-який промінь з
,
будь-який промінь з
![]() ,
,
![]() вимірні.
вимірні.
![]() ,
,
![]() .
.
5.
Відображення, що визначається функцією
![]() фіксоване дійсне число, називається
зсувом.
фіксоване дійсне число, називається
зсувом.
При
зсуві будь-який інтервал переходить в
інтервал тієї ж довжини. Дійсно, якщо
![]() задовольняє нерівність
задовольняє нерівність
![]() ,
то
,
то
![]() .
Отже образом інтервала
.
Отже образом інтервала
![]() буде інтервал
буде інтервал
![]() тієї ж довжини. Аналогічно доводиться,
що будь-який півінтервал або сегмент
перетворюється у півінтервал або сегмент
тієї ж довжини. Зсув є взаємно однозначним
перетворенням, тому елементарні множини
переходять в елементарні тієї ж міри.
Отже при зсуві зовнішня міра множин не
змінюється, вимірні за Лебегом множини
переходять у вимірні тієї ж міри.
тієї ж довжини. Аналогічно доводиться,
що будь-який півінтервал або сегмент
перетворюється у півінтервал або сегмент
тієї ж довжини. Зсув є взаємно однозначним
перетворенням, тому елементарні множини
переходять в елементарні тієї ж міри.
Отже при зсуві зовнішня міра множин не
змінюється, вимірні за Лебегом множини
переходять у вимірні тієї ж міри.
