
- •Теорія міри та інтеграла лебега
- •Глава I
- •1.1. Поняття множини, операції над множинами
- •Задачі.
- •1.2. Поняття відображення і взаємно однозначначної відповідності
- •Задачі.
- •3.1. Зчислені множини та їх властивості
- •Множини потужності континууму
- •Двійкові дроби.
- •Приклади важливих множин потужності континууму.
- •5.1 Існування потужності більшої, ніж с
- •Застосування теореми Бернштейна
- •Задачі.
- •Глава II
- •Властивості відкритих і замкнених множин
- •Глава III
- •3.1. Елементарні множини та їх властивості
- •. Міра елементарних множин та її властивість
- •3.3 Поняття зовнішньої міри обмеженої множини і її властивості.
- •3.4 Поняття вимірної множини
- •3.5 Поняття внутрішньої міри обмеженої множини.
- •Приклади вимірних множин і невимірної множини.
- •Приклад невимірної обмеженої множини.
- •3.6. Поняття півкільця, кільця, -алгебри
- •3.7. Поняття вимірної множини в
- •Узагальнення поняття вимірності в
- •3.8 Загальне поняття міри
- •Глава iy
- •Означення вимірної функції.
- •4.2.1 Приклади вимірних функцій
- •4.3.1. Загальні властивості вимірних функцій
- •4.4.1. Властивості вимірних функцій пов’язані з алгебраїчними операциями
- •4.5.1. Граничний перехід у класі вимірних функцій
- •Глава y
- •5.1. Означення інтеграла Лебега для простої функції і його властивості.
- •Приклади простих функцій інтегровних за Лебегом
- •Властивості інтеграла Лебега від простих функцій
- •5.2. Інтеграл Лебега і його властивості у загальному випадку.
- •Властивості інтеграла Лебега у загальному випадку
- •5.3. Граничний перехід під знаком інтеграла Лебега
- •5.4 Порівняння інтегралів Рімана і Лебега
- •5.5. Інтеграл Лебега по множені нескінченної міри
3.3 Поняття зовнішньої міри обмеженої множини і її властивості.
Означення
3.3.1
Нехай
![]()
довільна обмежена множина з
довільна обмежена множина з
![]() .
Число
.
Число
![]() ,
(3.3.1)
,
(3.3.1)
де
точна нижня межа береться по усім
скінченним або зчисленним об’єднанням
елементарних множин
![]() ,
називається зовнішньою мірою обмеженої
множини
,
називається зовнішньою мірою обмеженої
множини
![]() .
.
Властивості зовнішній міри.
1. Зовнішня міра невід’ємна.
2. Зовнішня
міра елементарної множини
![]() збігається з
збігається з
![]() ,
тобто
,
тобто
![]() .
.
Доведення.
Якщо
![]() ,
то в силу властивості 2 міри елементарних
множин,
,
то в силу властивості 2 міри елементарних
множин,
![]() і слід
і слід
![]() .
З іншого боку
.
З іншого боку
![]() тому, що
тому, що
![]() входить в множину по якої обчислюється
точна нижня межа.
входить в множину по якої обчислюється
точна нижня межа.
3. Якщо
обмежена множина
![]()
![]() ,
то
,
то
![]() .
.
Ця властивість випливає з означення зовнішньої міри і називається монотонністю.
-
Якщо обмежена множина

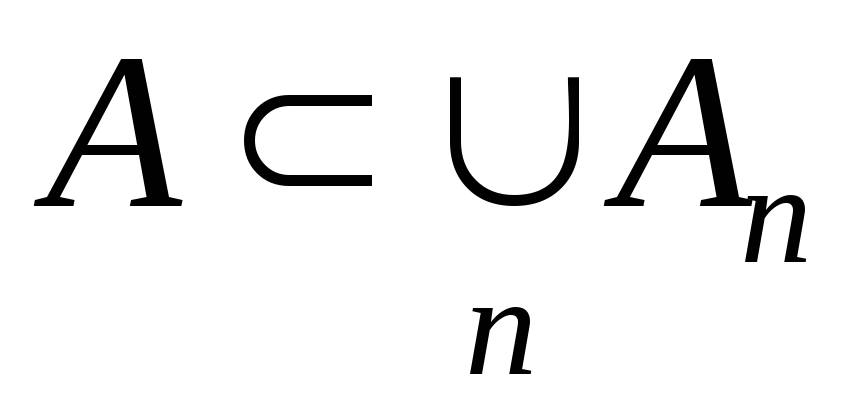 ,
де
,
де
 скінченна,
або зчисленна сім’я
множин, то
скінченна,
або зчисленна сім’я
множин, то
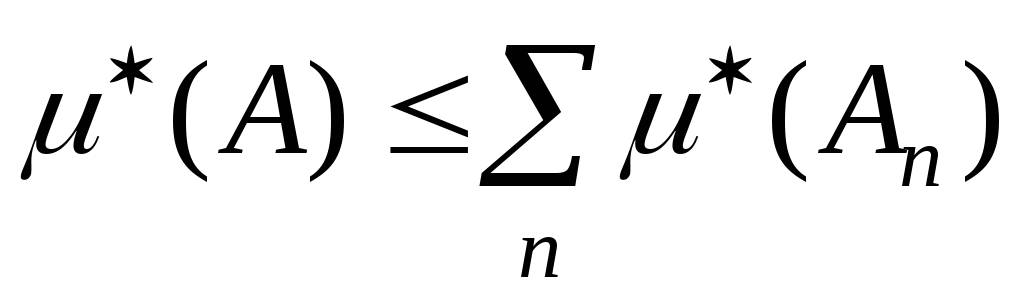 .
.
Доведення.
В силу властивості точної нижньої межі
для кожної множини
![]() і довільного числа
і довільного числа
![]() знайдеться скінченна, або зчисленна
система елементарних множин
знайдеться скінченна, або зчисленна
система елементарних множин
![]() така,
що
така,
що
![]() і
і
![]() .
Тоді
.
Тоді
![]() і
і
![]() .
.
Спрямувавши до нуля, одержимо указану властивість.
-
Для будь-яких обмежених множин
 і
і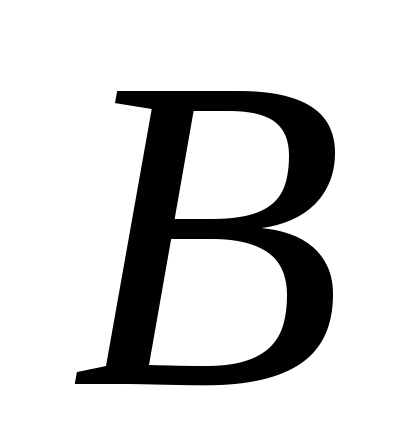 має
місце нерівність
має
місце нерівність
![]() .
(3.3.2)
.
(3.3.2)
Доведення.
Використовавши співвідношення
![]() і попередню властивість, одержимо
і попередню властивість, одержимо
![]() .
Помінявши місцями
.
Помінявши місцями
![]() і
і![]() одержимо
одержимо
![]() і отже маємо (3.3.2).
і отже маємо (3.3.2).
3.4 Поняття вимірної множини
Означення
3.4.1
Обмежена множина
![]() називається вимірною, якщо для довільного
числа
називається вимірною, якщо для довільного
числа
![]() знайдеться елементарна множина
знайдеться елементарна множина
![]() така, що
така, що
![]() .
.
Якщо
множина
![]() вимірна, то її мірою називається
вимірна, то її мірою називається
![]() .
Міра позначається символом
.
Міра позначається символом
![]() і називається мірою Лебега.
і називається мірою Лебега.
Із
означення вимірної множини випливає,
що будь-яка елементарна множина
![]() вимірна
і у сенсі останнього означення і
вимірна
і у сенсі останнього означення і
![]() .
.
Властивості вимірних множин.
1. Якщо
множина
![]() вимірна, то вимірне доповнення множина
до відрізка
вимірна, то вимірне доповнення множина
до відрізка
![]() .
.
Доведення випливає з рівності
![]() .
.
2. Об’єднання скінченної сім’ї вимірних множин є множина вимірна.
Доведення.
Розглянемо спочатку дві множини
![]() і
і![]() .
Для будь-якого числа
.
Для будь-якого числа
![]() знайдуться елементарні множини
знайдуться елементарні множини
![]() і
і![]() такі, що
такі, що
![]() і
і
![]() .
.
Так як об’єднання скінченної множини елементарних множин є елементарна множина, то, використовуючи включення
![]()
і властивості 3,4 зовнішньої міри, одержимо.
![]() .
.
Припустивши
вимірність об’єднання
![]() вимірних множин , в силу рівності
вимірних множин , в силу рівності
![]() одержимо вимірність множини
одержимо вимірність множини
![]() .
Завдяки принципу математичної індукції
вимірною буде скінченне об’єднання
вимірних множин.
.
Завдяки принципу математичної індукції
вимірною буде скінченне об’єднання
вимірних множин.
3. Перетин скінченної сім’ї вимірних множин є множина вимірна.
Доведення
і в цьому випадку достатньо провести
для двох множин
![]() і
і
![]() .
Розглянемо доповнення множини
.
Розглянемо доповнення множини
![]() до інтервалу
до інтервалу
![]() .
Внаслідок двоїстості операцій об’єднання
і перетину
.
Внаслідок двоїстості операцій об’єднання
і перетину
![]() .
.
За
властивостю 1 доданки у правій частині
вимірні, і завдяки властивості 2 вимірна
права частина, а тоді за властивістю 1
вимірна множина
![]() тому, що
тому, що
![]()
4. Різниця
![]() вимірних множин є множина вимірна.
вимірних множин є множина вимірна.
Доведення.
Нехай інтервал
![]() .
Тоді
.
Тоді
![]() і
отже, внаслідок властивостей 1 і 3, різниця
– вимірна.
і
отже, внаслідок властивостей 1 і 3, різниця
– вимірна.
5.
Симетрична
різниця вимірних множин![]() і
і![]() є множина вимірна.
є множина вимірна.
Ця властивість випливає з останньої властивості, властивості 2 і рівності
![]() .
.
6.
Адитивність міри. Міра об’єднання
скінченної сім’ї вимірних попарно
неперетинних множин
![]() ,
дорівнюю сумі мір, тобто
,
дорівнюю сумі мір, тобто
![]() .
.
Доведення.
Спочатку розглянемо дві множини
![]() і
і
![]()
загальний випадок легко одержимо методом
математичної індукції. Перш за все,
використовуючи властивість 4 зовнішньої
міри, одержимо
загальний випадок легко одержимо методом
математичної індукції. Перш за все,
використовуючи властивість 4 зовнішньої
міри, одержимо
![]() (3.4.1)
(3.4.1)
За
означенням вимірності, для будь-якого
числа
![]() знайдемо елементарні множини
знайдемо елементарні множини
![]() і
і![]() такі, що
такі, що
![]() і
і
![]() .
(3.4.2)
.
(3.4.2)
Надалі
значок, що позначає зовнішню міру,
будемо опускати тому, що усі множини
вимірні. Розглянемо наступні співвідношення
і нерівності. Оскільки множини
![]() і
і![]() не перетинаються, то
не перетинаються, то
![]()
і, тим більше,
![]() .
.
А тоді, внаслідок (3.4.2)
![]() (3.4.3)
(3.4.3)
З властивості 5 зовнішньої міри (див. нерівність (3.3.2)) випливає, що
![]() ,
(3.4.4)
,
(3.4.4)
![]() ,
(3.4.5)
,
(3.4.5)
і, аналогічно, використовуючи включення
![]() ,
,
одержимо
![]()
![]() .
(3.4.6)
.
(3.4.6)
Завдяки адитивності міри елементарних множин (див. наслідок 3)
![]() .
(3.4.7)
.
(3.4.7)
Застосуємо спочатку нерівність (3.4.6), потім рівність (3.4.7) і на кінець нерівності (3.4.3 – 3.4.5)
![]()
![]() .
.
В силу довільності одержимо нерівність
![]() ,
,
що разом з (3.4.1) дає необхідну рівність.
Припустимо
тепер, що властивість має місце для
![]() вимірних попарно неперетинних множин
вимірних попарно неперетинних множин
![]() тобто
тобто
![]() .
.
Розглянемо
далі
![]() вимірних попарно неперетинних множин
вимірних попарно неперетинних множин
![]() .
Тоді, внаслідок властивості для двох
множин і припущення одержимо
.
Тоді, внаслідок властивості для двох
множин і припущення одержимо
![]() .
.
За
принципом математичної індукції,
адитивність має місце до будь-якої
кількості вимірних попарно неперетинних
множин
![]() .
.
Наслідок
1.
Якщо
![]() і
і![]()
вимірні множини і
вимірні множини і
![]() ,
то
,
то
![]() .
.
Доведення аналогічно доведенню такої ж властивості міри елементарних множин.
Наслідок
2.
Якщо
![]() і
і![]()
вимірні множини, то
вимірні множини, то
![]() .
(3.4.8)
.
(3.4.8)
Доведення.
Зобразимо
об’єднання
множин
![]() і
і![]() у
вигляді
у
вигляді
![]()
Множини
![]() і
і![]() не перетинаються, тому на підставі
властивості 6
не перетинаються, тому на підставі
властивості 6
і наслідку 1, маємо
![]() .
.
Рівність (3.4.8) у теорії ймовірностей називається теоремою додавання.
Наслідок
3.
Якщо
![]() і
і![]()
довільні обмежені множини, то
довільні обмежені множини, то
![]() .
(3.4.9)
.
(3.4.9)
Доведення.
В
силу властивості точної нижньої межі
для кожної з множин
![]() і
і![]() та довільного числа
та довільного числа
![]() знайдеться скінченна, або зчисленна
система елементарних множин
знайдеться скінченна, або зчисленна
система елементарних множин
![]() така,
що
така,
що
![]()
![]() і
і
![]() .
.
Тоді на підставі наслідку 2
![]()
![]() .
.
Спрямувавши до нуля, одержимо (3.4.9).
7.
Обмежено
об’єднання зчисленної сім’ї вимірних
попарно неперетинних множин
![]() є множина вимірна.
є множина вимірна.
Доведення.
Нехай
![]() .
Тоді, в силу адитивності міри і обмеженості
множини
.
Тоді, в силу адитивності міри і обмеженості
множини
![]() :
:
![]() .
Отже ряд
.
Отже ряд
![]() збігається. Тоді для
довільного
числа
збігається. Тоді для
довільного
числа
![]() знайдеться натуральне число
знайдеться натуральне число
![]() таке, що
таке, що
![]() .
Внаслідок властивості 4 зовнішньої
міри, одержимо
.
Внаслідок властивості 4 зовнішньої
міри, одержимо
![]() (3.4.10)
(3.4.10)
Оскільки
множина
![]() вимірна, то існує елементарна множина
вимірна, то існує елементарна множина
![]() така, що
така, що
![]() .
(3.4.11)
.
(3.4.11)
Тоді з нерівностей (3.4.10 – 3.4.11) і співвідношення
![]()
випливає
![]() .
Одже множина
.
Одже множина
![]() є вимірною.
є вимірною.
8. Обмежено
об’єднання зчисленної сім’ї вимірних
множин
![]() є вимірна множина.
є вимірна множина.
Доведення.
Нехай
![]() і
і
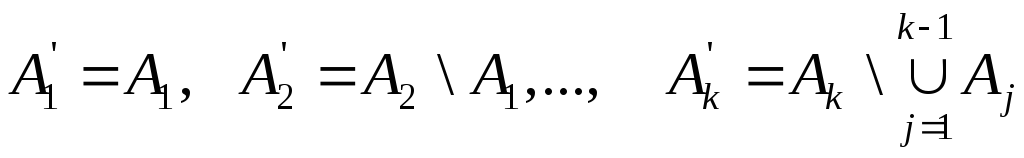 .
Множини
.
Множини
![]() попарно не перетинаються, вимірні і, як
легко перевірити,
попарно не перетинаються, вимірні і, як
легко перевірити,
![]() .
Отже, внаслідок попередньої властивості,
.
Отже, внаслідок попередньої властивості,
![]() вимірна
множина.
вимірна
множина.
Наслідок
4. Якщо
виконуються умови властивості 8, то
![]() .
.
Доведення.
![]() .
.
9.
Перетин
зчисленної
сім’ї вимірних множин
![]() є множина вимірна.
є множина вимірна.
Доведення.
Нехай
![]() і інтервал
і інтервал
![]() .
Тоді
.
Тоді
![]() і, внаслідок властивості 6, множина
і, внаслідок властивості 6, множина
![]() вимірна,
одже множина
вимірна,
одже множина
![]() є вимірною.
є вимірною.
10. Міра
обмеженого об’єднання зчисленної
сім’ї вимірних попарно неперетинних
множин
![]() множин дорівнює сумі мір.
множин дорівнює сумі мір.
Доведення.
Нехай
![]() .
Тоді з одного боку, в силу властивості
зовнішньої міри,
.
Тоді з одного боку, в силу властивості
зовнішньої міри,
![]() ,
,
а з іншого
![]()
Отже
![]() .
.
11. Нехай
вимірні множини
![]() такі, що
такі, що
![]() Тоді
Тоді
![]() .
.
Доведення.
Внаслідок монотонності послідовності
множин, множини
![]() попарно неперетинні і виконується
рівність
попарно неперетинні і виконується
рівність
![]() .
.
Використовуючи попередню властивість і наслідок з властивості 6, одержимо
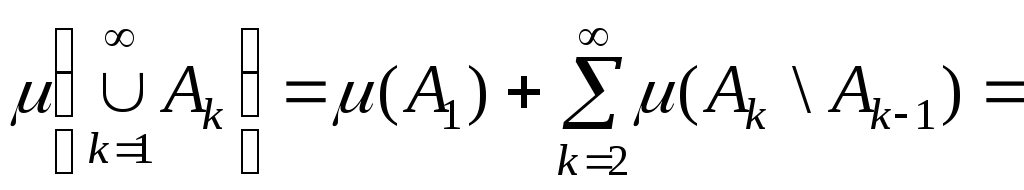
![]() .
.
12. Нехай
вимірні множини
![]() такі, що
такі, що
![]() Тоді
Тоді
![]() .
.
Доведення.
Внаслідок монотонності послідовності
множин, множини
![]() задовольняють умову попередньої
властивості. Отже
задовольняють умову попередньої
властивості. Отже
![]() .
.
Внаслідок співвідношень двоїстості одержимо
![]()
![]() .
.
13. Нехай
множини
![]() такі, що
такі, що
![]() Тоді
Тоді
![]() .
(3.4.12)
.
(3.4.12)
Доведення.
Внаслідок обмеженості і монотонності
послідовності множин і монотонності
зовнішньої міри
![]() існує і
існує і
![]() .
(3.4.13)
.
(3.4.13)
Щоб
довести протилежну нерівність, для
кожної множини
![]() і довільного числа
і довільного числа
![]() знайдемо скінченну, або зчисленну
систему елементарних множин
знайдемо скінченну, або зчисленну
систему елементарних множин
![]() таких,
що
таких,
що
![]() і
і
![]() .
Нехай
.
Нехай
![]() .
Очевидно, що
.
Очевидно, що
![]()
![]() і
і
![]() .
Використовуючи вимірність множин
.
Використовуючи вимірність множин
![]() і властивість 11, одержимо
і властивість 11, одержимо
![]()
![]() .
.
Завдяки довільності числа , маємо
![]() ,
,
Що разом з (3.4.13) дає рівність (3.4.12).
Захід, за допомогою якого визначена міра Лебега на множинах, більш загальних за елементарні множина, називається продовженням міри за Лебегом.
