5.3. Граничний перехід під знаком інтеграла Лебега

Теорема 5.3.1 (Теорема Лебега). Нехай послідовність вимірних майже скрізь скінченних на множині функцій збігається за мірою до майже скрізь скінченної функції і існує невід’ємна інтегровна за Лебегом функція така, що майже скрізь на множині : . Тоді функція інтегровна за Лебегом на множині і

. (5.3.1)

Доведення. На підставі теореми Рісса існує підпослідовність , що збігається майже скрізь на множині до функції. Тоді функція вимірна і оскільки майже скрізь на множині , то функція на підставі властивості 6 інтегровна за Лебегом на множині . Приступаючи до доведення рівності (5.3.1) зауважимо, що можливо вважати, що міра множини більша нуля, бо в протилежному випадку інтеграли у рівності (5.3.1) дорівнюють нулю і рівність очевидна. Для довільного числа візьмемо таке число , що . Нехай і . Використовуючи адитивність інтеграла, властивість 6 і нерівність , яка виконується майже скрізь, одержимо

(5.3.2)

Щоб оцінити перший доданок у правій частини нерівності (5.3.2) застосуємо властивість 6:

Для заданого , внаслідок абсолютної неперервності інтеграла від функції , знайдемо таке , що

, (5.3.3)

якщо . Оскільки послідовність функцій збігається за мірою до функції , то міра множини прямує до нуля, тому знайдеться число таке, що для усіх має місце нерівність . Отже, для усіх має місце нерівність

. (5.3.4)

Таким чином із нерівностей (5.3.3)  (5.3.4) для усіх випливає нерівність

.

Теорема доведена.

Наслідок 5.3.1 Нехай послідовність вимірних на множині функцій збігається майже скрізь до функції і існує невід’ємна інтегровна за Лебегом функція така, що майже скрізь на множині : . Тоді функція інтегровна за Лебегом на множині і має місце рівність (5.3.1).

Доведення. За теоремою Лебега (див. теорему 4.1.4) послідовність функцій збігається за мірою до функції . Слід виконуються умови теореми 5.3.1.

Ще більш простий варіант теореми Лебега одержимо, якщо функцію замінимо константою.

Наслідок 5.3.2 Нехай послідовність вимірних на множині функцій збігається майже скрізь до функції і існує константа така, що майже скрізь на множині : . Тоді функція інтегровна за Лебегом на множині і має місце рівність (5.3.1).

Доведення. Якщо послідовність вимірних на множині функцій збігається майже скрізь до функції , то за теоремою Лебега (див. теорему 4.1.4) послідовність функцій збігається за мірою до функції . Отже виконуються умови теореми 5.3.1.

Теорема 5.3.2 (теорема Леві). Нехай  неспадаюча послідовність невід’ємних інтегровних на множині функцій така, що для усіх

. (5.3.5)

Тоді майже скрізь на множині послідовність збігається до майже скрізь скінченної інтегрованої функції і

. (5.3.6)

Доведення. З монотонності послідовності функцій випливає існування , покажемо, що майже скрізь ця границя скінченна.

Введемо множину і покажемо, що . Для довільного числа множина . Дійсно, якщо , то існує натуральне число таке, що для усіх виконується нерівність . Отже . Завдяки тому, що послідовність не спадає, і тоді . Внаслідок нерівності Чебишева і умови теореми . Отже і для будь-якого : . Отже .

Нехай . Множини вимірні, попарно неперетинні і 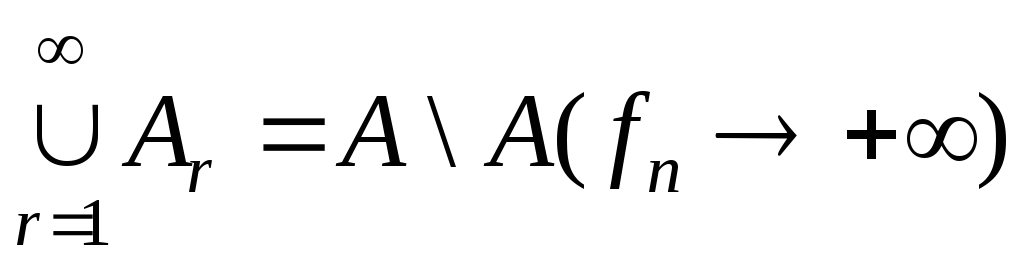. На множені визначимо просту функцію , якщо і покажемо, що вона інтегровна на множені , тобто доведемо збіжність ряду . Позначимо через і оцінимо частину суму . Із означення функції випливає нерівність

. (5.3.7)

Використовуючи нерівність (5.3.7), наслідок 2 і умову (5.3.5) одержимо

=

.

Отже функція інтегровна на множені і . Таким чином для послідовності функцій виконуються умови наслідку 1. Тоді функція інтегровна на множені і має місце рівність (5.16).

Теорема доведена.

Наслідок 5.3.3. Твердження теореми Леві збережеться, якщо функції послідовності приймають значення різних знаків. Щоб довести це, треба ввести функції і константу в умові (5.3.5) замінити на . Тоді функція інтегровна на множені і має місце рівність:

.

Порівнюючи початок і кінець рядка рівностей одержимо (5.3.6).

Наслідок 5.3.4. Нехай послідовність невід’ємних і інтегровних на множені функцій таких, що ряд

збігається. Тоді сума ряду є функція інтегровна на множені і

=. (5.3.8)

Доведення. Нехай . Оскільки послідовність невід’ємних і інтегровних на множені функцій, то неспадаюча, послідовність невід’ємних і інтегровних на множені функцій таких, що

.

Отже виконуються умови теореми Леві, застосовуючи яку одержимо (5.3.8).

Теорема 5.3.3 (теорема Фату). Нехай  послідовність невід’ємних інтегровних на множині функцій, яка майже скрізь на множині збігається до функції і така, що для усіх

. (5.3.9)

Тоді функція інтегровна на множині і

. (5.3.10)

Доведення. Нехай Функції вимірні на множені , тому, що . Оскільки , то невід’ємні і інтегровні на множині . Крім того, і, за умовою (5.3.9)

. (5.3.11)

Отже для послідовності функцій виконуються умови теореми Леві, за якою функція інтегровна на множені і, внаслідок (5.3.11)

.

Покажемо, що якщо послідовність збігається до , то послідовність теж збігається до . Нехай довільне додатне число. Існує число таке, що для будь-якого виконується нерівність . Тоді

для усіх виконується нерівність . Отже . Так як функція майже скрізь скінченна, то і така ж сама.

Покажемо тепер, що якщо , то . Нехай . Знайдеться число таке, що для будь-якого виконуються нерівності . Тоді, очевидно, що і для усіх виконується нерівність . Отже для усіх виконується нерівність

,

Тобто майже скрізь і має місце нерівність (5.3.10).

Теорема доведена.