
- •Теорія міри та інтеграла лебега
- •Глава I
- •1.1. Поняття множини, операції над множинами
- •Задачі.
- •1.2. Поняття відображення і взаємно однозначначної відповідності
- •Задачі.
- •3.1. Зчислені множини та їх властивості
- •Множини потужності континууму
- •Двійкові дроби.
- •Приклади важливих множин потужності континууму.
- •5.1 Існування потужності більшої, ніж с
- •Застосування теореми Бернштейна
- •Задачі.
- •Глава II
- •Властивості відкритих і замкнених множин
- •Глава III
- •3.1. Елементарні множини та їх властивості
- •. Міра елементарних множин та її властивість
- •3.3 Поняття зовнішньої міри обмеженої множини і її властивості.
- •3.4 Поняття вимірної множини
- •3.5 Поняття внутрішньої міри обмеженої множини.
- •Приклади вимірних множин і невимірної множини.
- •Приклад невимірної обмеженої множини.
- •3.6. Поняття півкільця, кільця, -алгебри
- •3.7. Поняття вимірної множини в
- •Узагальнення поняття вимірності в
- •3.8 Загальне поняття міри
- •Глава iy
- •Означення вимірної функції.
- •4.2.1 Приклади вимірних функцій
- •4.3.1. Загальні властивості вимірних функцій
- •4.4.1. Властивості вимірних функцій пов’язані з алгебраїчними операциями
- •4.5.1. Граничний перехід у класі вимірних функцій
- •Глава y
- •5.1. Означення інтеграла Лебега для простої функції і його властивості.
- •Приклади простих функцій інтегровних за Лебегом
- •Властивості інтеграла Лебега від простих функцій
- •5.2. Інтеграл Лебега і його властивості у загальному випадку.
- •Властивості інтеграла Лебега у загальному випадку
- •5.3. Граничний перехід під знаком інтеграла Лебега
- •5.4 Порівняння інтегралів Рімана і Лебега
- •5.5. Інтеграл Лебега по множені нескінченної міри
5.4 Порівняння інтегралів Рімана і Лебега
Нехай
![]() обмежена
функція, визначена на сегменті
обмежена
функція, визначена на сегменті
![]() ,
тобто
,
тобто
![]() ,
(5.4.1)
,
(5.4.1)
і
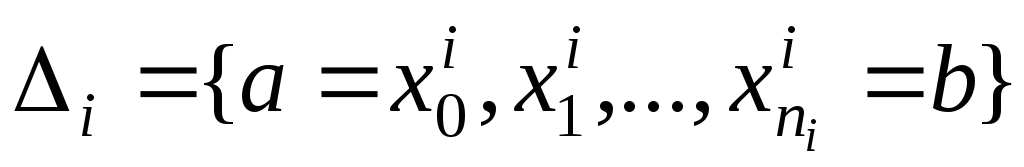
послідовність наборів точок сегменту
послідовність наборів точок сегменту
![]() таких, що
таких, що![]() .
Покладемо
.
Покладемо
![]() ,
,
![]()
![]() і визначимо дві послідовності простих
функцій:
і визначимо дві послідовності простих
функцій:
![]() ,
,
![]() .
Із означення функцій
.
Із означення функцій
![]() ,
,
![]() і (5.4.1) випливає
і (5.4.1) випливає
![]() .
(5.4.2)
.
(5.4.2)
Отже,
функції
![]() ,
,
![]()
прості і обмежені і слід інтегровні за
Лебегом:
прості і обмежені і слід інтегровні за
Лебегом:![]()
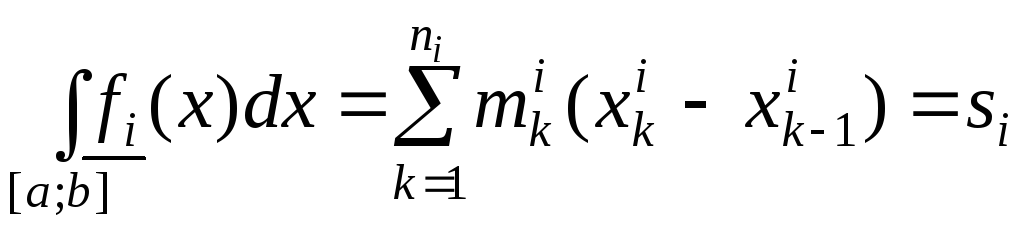 ,
,
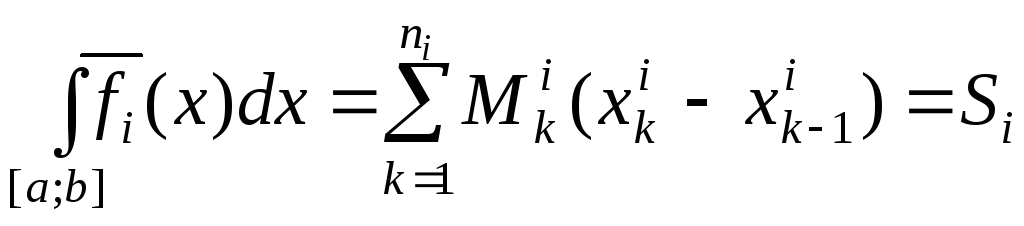 ,
,
де
![]() відповідно нижня і верхня суми Дарбу
функції
відповідно нижня і верхня суми Дарбу
функції
![]() .
Оскільки при умові
.
Оскільки при умові
![]() виконуються нерівності
виконуються нерівності
![]() ,
то послідовність функцій
,
то послідовність функцій
![]() не спадає, а послідовність функцій
не спадає, а послідовність функцій![]() не зростає. Отже для послідовностей
функцій
не зростає. Отже для послідовностей
функцій
![]() і
і
![]() виконуються умови теореми Леві, за якою
існують майже скрізь границі
виконуються умови теореми Леві, за якою
існують майже скрізь границі
![]() і
і
![]() ,
функції
,
функції
![]() і
і
![]() інтегровні за Лебегом на сегменті
інтегровні за Лебегом на сегменті
![]() і
і
![]() ,
(5.4.3)
,
(5.4.3)
![]() .
(5.4.4)
.
(5.4.4)
Окрім
того, із нерівностей (5.4.2) випливає, що
для функцій
![]() і
і
![]() мають місце нерівності
мають місце нерівності
![]() .
(5.4.5)
.
(5.4.5)
Із (5.4.3) – (5.4.5) одержимо
![]() .
(5.4.6)
.
(5.4.6)
Теорема
5.4.1 Для
того щоб функція
![]() була
інтегровною за Ріманом необхідно і
досить, щоб
була
інтегровною за Ріманом необхідно і
досить, щоб
![]() майже скрізь на сегменті
майже скрізь на сегменті
![]() для будь-якої послідовності
для будь-якої послідовності
![]() такої, що
такої, що
![]() ,
коли
,
коли
![]() і в цьому випадку функція
і в цьому випадку функція
![]() інтегровна за Лебегом і інтеграл Рімана
збігається з інтегралом Лебега:
інтегровна за Лебегом і інтеграл Рімана
збігається з інтегралом Лебега:
![]() .
.
Достатність.
Нехай
![]() .
Тоді, внаслідок (5.4.6), інтеграл в (5.4.6)
дорівнює нулю і
.
Тоді, внаслідок (5.4.6), інтеграл в (5.4.6)
дорівнює нулю і
![]() .
Отже функція
.
Отже функція
![]() інтегровна за Ріманом.
інтегровна за Ріманом.
Необхідність.
Нехай
функція
![]() інтегровна за Ріманом. Тоді для будь-якої
послідовності
інтегровна за Ріманом. Тоді для будь-якої
послідовності
![]() такої, що
такої, що
![]() ,
права частина в (5.4.6) дорівнює нулю. На
підставі наслідку 5.2.2 (з нерівності
Чебишева) різниця
,
права частина в (5.4.6) дорівнює нулю. На
підставі наслідку 5.2.2 (з нерівності
Чебишева) різниця
![]() майже скрізь дорівнює нулю. А тоді із
нерівностей (5.4.5) випливає еквівалентність
функції
майже скрізь дорівнює нулю. А тоді із
нерівностей (5.4.5) випливає еквівалентність
функції
![]() функціям
функціям
![]() і
і![]() .
Отже, функція
.
Отже, функція
![]() інтегровна за Лебегом і, в силу (5.4.3) або
(5.4.4), інтеграл Рімана збігається з
інтегралом Лебега.
інтегровна за Лебегом і, в силу (5.4.3) або
(5.4.4), інтеграл Рімана збігається з
інтегралом Лебега.
Теорема
5.4.2 (Теорема Лебега). Для
того щоб обмежена функція
![]() була інтегровною за Ріманом на сегменті
була інтегровною за Ріманом на сегменті
![]() ,
необхідно і досить, щоб
,
необхідно і досить, щоб
![]() була майже скрізь неперервною на
сегменті
була майже скрізь неперервною на
сегменті
![]() .
.
Достатність.
Нехай
![]() майже
скрізь неперервна на сегменті
майже
скрізь неперервна на сегменті
![]() і
і
![]() множина
точок розриву. Візьмемо будь-яку
послідовність
множина
точок розриву. Візьмемо будь-яку
послідовність
![]() точок розбиття таку, що
точок розбиття таку, що
![]() і нехай
і нехай
![]() .
Множина
.
Множина
![]() зчисленна, тому
зчисленна, тому
![]() має міру нуль. Покажемо, що у кожній
точці
має міру нуль. Покажемо, що у кожній
точці
![]() має місце рівність
має місце рівність
![]() .
Візьмемо довільне число
.
Візьмемо довільне число
![]() .
Внаслідок неперервності функції
.
Внаслідок неперервності функції
![]() в точці
в точці
![]() існує
існує
![]() таке, що
таке, що
![]() ,
якщо
,
якщо
![]() .
Оскільки
.
Оскільки
![]() ,
то знайдеться натуральне число
,
то знайдеться натуральне число
![]() таке,
що для усіх
таке,
що для усіх
![]() сегменти
сегменти
![]() ,
що містять точку
,
що містять точку
![]() ,
будуть міститься в інтервалі
,
будуть міститься в інтервалі
![]() .
Тоді, для усіх
.
Тоді, для усіх
![]() різниця
різниця
![]()
![]() ,
тобто
,
тобто
![]() майже
скрізь. За теоремою 5.4.1 функція
майже
скрізь. За теоремою 5.4.1 функція
![]() інтегровна за Ріманом.
інтегровна за Ріманом.
Необхідність.
Нехай
функція
![]() інтегровна за Ріманом. За теоремою 5.4.1
і, в силу (5.4.5),
інтегровна за Ріманом. За теоремою 5.4.1
і, в силу (5.4.5),
![]() майже
скрізь. Позначимо через
майже
скрізь. Позначимо через
![]() множину точок сегмента
множину точок сегмента
![]() ,
де
,
де
![]() .
Візьмемо будь-яку послідовність
.
Візьмемо будь-яку послідовність
![]() точок розбиття сегмента
точок розбиття сегмента
![]() таку, що
таку, що
![]() і нехай
і нехай
![]() .
Множина
.
Множина
![]() має міру нуль. Покажемо, що у кожній
точці
має міру нуль. Покажемо, що у кожній
точці
![]() функція
функція
![]() неперервна. Візьмемо довільне число
неперервна. Візьмемо довільне число
![]() .
В силу збіжності послідовностей функцій
.
В силу збіжності послідовностей функцій
![]() і
і
![]() відповідно до функцій
відповідно до функцій
![]() і
і
![]() знайдеться натуральне число
знайдеться натуральне число
![]() таке, що для усіх
таке, що для усіх
![]() виконуються нерівності
виконуються нерівності
![]() ,
,
із яких випливає нерівність
![]() (5.4.7)
(5.4.7)
Візьмемо
сегмент
![]() ,
що містить точку
,
що містить точку
![]() .
Оскільки
.
Оскільки
![]() не є точкою розбиття, то знайдеться
інтервал
не є точкою розбиття, то знайдеться
інтервал
![]() ,
що міститься у сегменті
,
що міститься у сегменті
![]() .
Із означення функцій
.
Із означення функцій
![]() ,
,
![]() і нерівності (5.4.7) маємо
і нерівності (5.4.7) маємо
![]()
для
будь-якого
![]() .
.
Теорема доведена.
