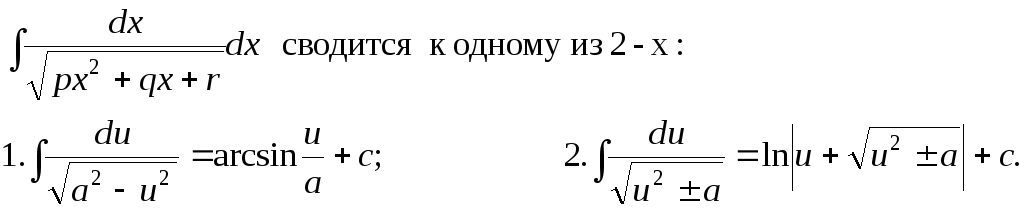- •11.Непрерывность функции
- •13.Правила диферинцирования.
- •16. Производная неявной функции. Производные высших порядков.
- •17. Теорема Ферма
- •Геометрический смысл теоремы
- •Доказательство
- •Доказательство
- •20. Правило Лопиталя
- •37 Геометрическое приложение определенного интеграла
- •38 Несобственные интегралы
- •39 Фн. Нескольк. Переменных
- •42.Свойства непрерывной ф-ции
- •43.Частные производные. Понятие дифференцируемости функции. Необходимые условия диф-ти.
- •45. Производные частных функций
- •55. Дифференциальные уравнения первого порядка. Теорема о существовании и единственности решения с разделяющимися переменными.
- •61. Интегрирующий множитнль
- •63. Типы уравнений, допускающих понижение порядка
- •64. Линейное однородное диф-ое ур-ие высших порядков.
- •65. Линейная зависимость ф-ий. Определитель Вронского и его свойства
- •71. Основные понятия. Сходимость ряда. Свойства сходящихся рядов.
- •72. Необходимый признак сходимости. Гармонический ряд.
- •73.Ряды с положительными членами. Признак сравнения.
- •74.Предельный признак сравнения. Признак Даламбера.
- •75. Интегральный признак сходимости Коши.
- •76. Знакочередующиеся ряды.Признак Лейбница. Знакопеременные ряды.
- •77. Степенные ряды.Теорема Абеля.
- •78. Радиус сходимости степенного ряда. Свойства степенных рядов.
- •Свойства степенных рядов:
- •79. Ряды Тейлора и Маклорена.
- •69.Способ неопределённых коэффициентов.
77. Степенные ряды.Теорема Абеля.
Степенной ряд:
![]() (1)
(1)
Коэфициент Сj- наз коэф степенного ряда. Совокупность тех значений X, при которых степенной ряд (1) сходится, наз областью сходимости степенного ряда.
Теорема
Абеля:
1) Если степенной ряд сходится при
значении
![]() и X
не равен 0, то он сходится, и притом
абсолютно, при всех значениях Х, таких
что
и X
не равен 0, то он сходится, и притом
абсолютно, при всех значениях Х, таких
что
![]() .
.
2)
Если степенной ряд расходится при
![]() , то он расходится при всех значениях
Х таких, что
, то он расходится при всех значениях
Х таких, что
![]() .
.
Доказательство
1:
По условию ряд (1) сходится при
![]() отсюда следует, что выполняется
необходимый презнак сходимости :
отсюда следует, что выполняется
необходимый презнак сходимости :![]() .
.
![]() -
ограничена, тоесть сущ такое число М>0,
что для всех n
выполняется неравенство:
-
ограничена, тоесть сущ такое число М>0,
что для всех n
выполняется неравенство:
![]() (2)
(2)
Рассмотрим ряд составленный из абсолютных величин членов ряда 1:
![]() ,
который представлен в виде:
,
который представлен в виде:
![]() (3)
(3)
Члены ряда (3) согласно неравенству (2) меньше соответственно членов ряда:ъ
![]()
представляющего
геометрич ряд, который сходится, когда
его знаменатель
![]()
тоесть
![]() ,
ряд (1) сходится по признаку сравнения.
,
ряд (1) сходится по признаку сравнения.
Доказательство
2: По
условию ряд (1) сходится при условии
Х=Х1. Покажем, что он расходится для всех
![]() .
Предположим противное, что при
.
Предположим противное, что при
![]() ряд (1) сходится, тогда по доказанному
выше он должен сходится и в точке Х1,
что противоречит условию, таким образом
для всех
ряд (1) сходится, тогда по доказанному
выше он должен сходится и в точке Х1,
что противоречит условию, таким образом
для всех
![]() ряд (1)- расходится.
ряд (1)- расходится.
78. Радиус сходимости степенного ряда. Свойства степенных рядов.
Из
теоремы Абеля следует, что сущ такое
число
![]() ,
что при
,
что при
![]() - ряд сходится, а при
- ряд сходится, а при
![]() -
ряд расходится.
-
ряд расходится.
Число R- наз радиусом сходимости, а интервал от (-R;R) – интервалом сходимости степенного ряда. На концах интервала сходимости ряд может сходится и расходится. Рассмотрим ряд (1), в составе которого абсолютные величины его членов:
![]() (4)
(4)
в котором все коэф Сn- отличны от 0.
По признаку Даламбера ряд (4) сходится при:
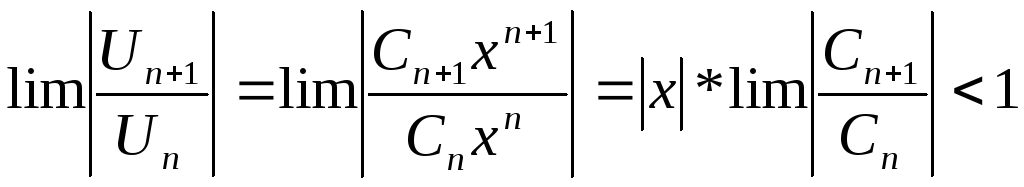
![]() -
если этот предел явл радиусом сходимости
степенного ряда:
-
если этот предел явл радиусом сходимости
степенного ряда:
![]() (5)
(5)
Свойства степенных рядов:
Пусть функция f(x) – сумма степенного ряда.
![]()
-
На любом отрезке АВ целиком пренадлежащем интервалу сходимости, ф-ия f(x) явл непрерывной, а отсюда следует, что степенной ряд можно почленно интегрировать на этом отрезке.
-
Кроме того, в интервале сходимости степенной ряд можно почленно диффиренцировать.
При этом после диффиренцирования или интегрирования, полученные ряды имеют тот же радиус сходимости R.
79. Ряды Тейлора и Маклорена.
Теорема:
Пусть функция f(x)
имеет в точке «а» и некоторые ее
окресности производные порядка
n+1.
Пусть Х- любое значение аргумента из
указанной окресности
![]() .
Тогда между т. а и х найдется точка
.
Тогда между т. а и х найдется точка
![]() такая, что справедлива следующая
формула:
такая, что справедлива следующая
формула:
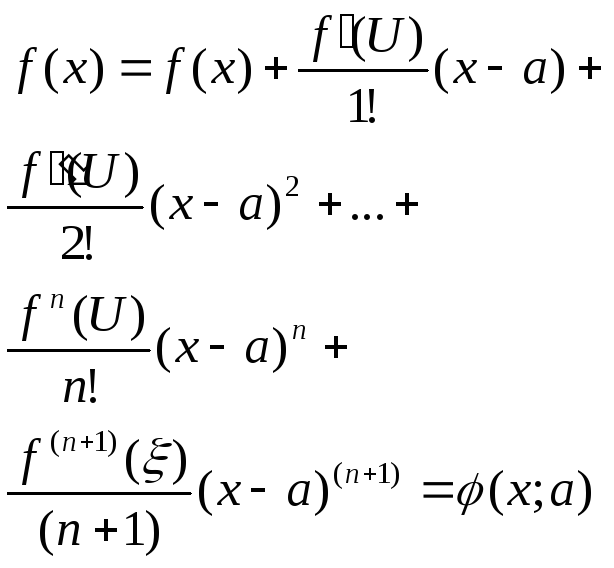 (1)
(1)
многочлен относительно Х формулы (1).
Обозначим
через
![]() ,
где:
,
где:
![]() ;
где
;
где
![]()
Фиксируем любое значение Хиз указанной окресности для определенности считаем, что х>a. Обозначим через t- переменную величину изменяющуюся на отрезке (а;х) и рассмотрим на этом отрезке вспомагательную ф-ию:
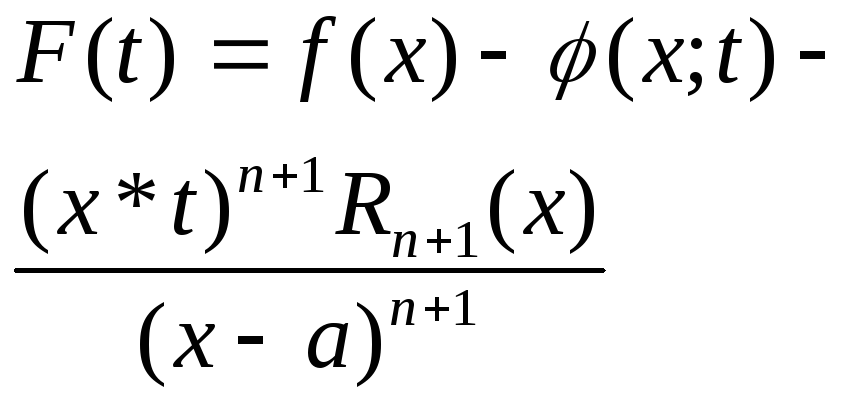 (2)
(2)
ф-ия F(t)- на отрезке (а;х) удовлетворяет всем условиям теоремы Ролля. Из формулы (2) и из условий наложенных на ф-ию f(x) , вытекает , что F(t)- непрерывна и диффиринцируема на отрезке (а;х).
 .
.
Пологая, что в (2) f=x , получим:
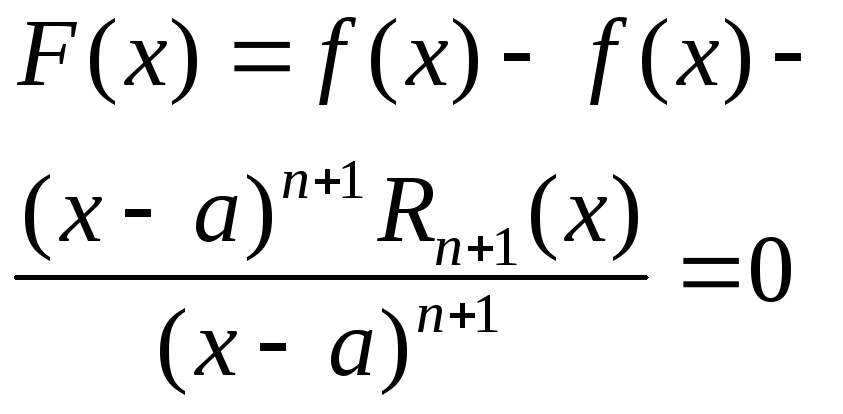
Внутри
отрезка (а;х) сущ т.![]() ,
такая что :
,
такая что :![]() (3)
(3)
Диффиринцируя равенство (3) по t получим:
 Член
в формуле Лагранжа.
Член
в формуле Лагранжа.
Формулой Маклорена наз формулу Тейлора для а=0:
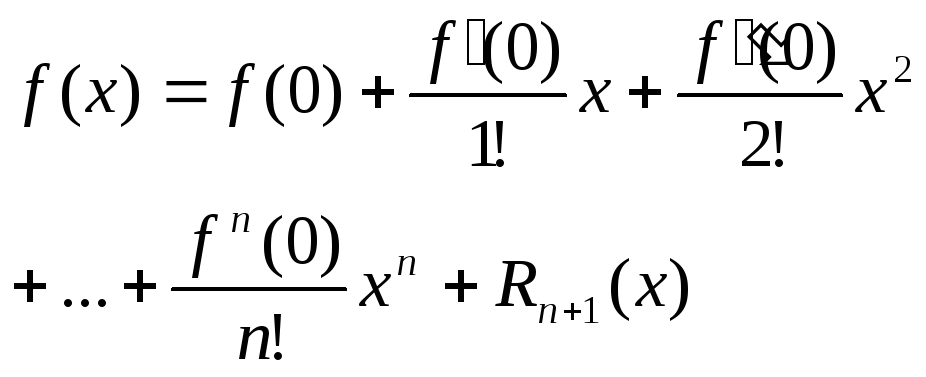
![]() ,
где
,
где
![]()
-
Понятие множества.
-
Понятие функции, ее свойства.
-
Элементарные функции. Классификация функций. Преобразование графике».
-
Предел числовой последовательности.
-
Предел фун в бесконечн и в точке.
-
Бесконечно малые величины.
-
Бесконечно большие величины.
-
Основные теоремы о пределах. Признаки существования предела.
-
Первый замечательный предел.
-
Второй замечательный предел.
-
Непрерывность функции. Свойства функций непрерывных в точке и на отрезке.
-
Определение производной. Зависимость между непрерывностью и дифференцируемостью функции.
-
Правила дифференцирования.
-
Производная сложной и обратной функций.
-
Производные основных элементарных функций.
-
Производная неявной функции. Производные высших порядков.
-
Теорема Ферма.
-
Теорема Роля.
-
Теорема Лагранжа.
-
Правило Лопиталя.
-
Возрастание и убывание функции.
-
Экстремум функции.
-
Выпуклость функции. Точки перегиба.
-
Асимптоты графика функции.
-
Дифференциал функции. Дифференциалы высших порядков.
-
Первообразная функции и неопределенный интеграл.
-
Свойства неопределенного интеграла,
-
Интегрирование разложением. Метод подстановки.
-
Метод интегрирования по частям.
-
Интегрирование некоторых функций, содержащих квадратный трехчлен.
-
Интегрирование рациональных функций.
-
Интегрирование тригонометрических функций.
-
Интегрирование некоторых иррациональных функций.
-
Понятие определенного интеграла, его геометрический смысл.
-
Свойства определенного интеграла.
-
Формула Ньютона-Лейбница. Замена переменной и формула интегрирования по частям в определенном интеграле.
-
Геометрические приложения определенного интеграла.
-
Несобственные интегралы.
-
Понятие функции нескольких переменных.
-
Геометрическое изображение функции двух переменных.
-
Предел функции двух переменных.
-
Непрерывность функции двух переменных. Свойства непрерывных функций.
-
Частные производные. Понятие дифференцируемости функции. Необходимые условия дифференцируемости.
-
Частные производные. Понятие дифференцируемости функции. Достаточное условие дифференцируемости.
-
Производные сложных функций.
-
Дифференциал функции.
-
Производная по направлению.
-
Градиент.
-
Частные производные и дифференциалы высших порядков.
-
Экстремумы функции двух переменных. Необходимое условие существования экстремума. Достаточное условие экстремума функции двух переменных.
-
Наибольшее и наименьшее значения функции.
-
Условный экстремум. Метод множителей Лагранжа.
-
Понятие об эмпирических формулах. Метод наименьших ква.
-
Дифференциальные уравнения. Основные понятия. Геометрическое истолкование.
-
Дифференциальные уравнения первого порядка. Теорема о существовании и единственности решения. Дифференциальные уравнения с разделяющимися переменными.
-
Однородные дифференциальные уравнения первого порядка и приводящиеся к ним.
-
Линейные дифференциальные уравнения первого порядка. Метод замены переменной.
-
Линейные дифференциальные уравнения первого порядка. Метод вариации произвольной постоянн
-
Уравнение Бернулли.
-
Уравнения в полных дифференциалах.
-
Интегрирующий множитель.
-
Дифференциальные уравнения высших порядков.
-
Типы уравнений, допускающих понижение порядка.
-
Линейные однородные дифференциальные уравнения высших порядков. Линейный дифференциальный оператор.
-
Линейная зависимость функций. Определитель Вронского и его сво.
-
Теорема об общем решении линейного однородного дифференциального уравнения.
-
Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
-
Линейные неоднородные дифференциальные уравнения. Теоремы об общем и частном решениях.
-
Линейные неоднородные дифференциальные уравнения. Метод неопределенных коэффициентов.
-
Линейные неоднородные дифференциальные уравнения. Метод вариации произвольных постоянных.
-
Основные понятия. Сходимость ряда. Свойства сходящихся рядов.
-
Необходимый признак сходимости. Гармонический ряд.
-
Ряды с положительными членами. Признак сравнения.
-
Предельный признак сравнения. Признак Даламбера.
-
Интегральный признак сходимости Коши.
-
Знакочередующиеся ряды. Признак Лейбница. Знакопеременные ряды.
-
Степенные ряды. Теорема Абеля.
-
Радиус сходимости степенного ряда. Свойства степенных рядов.
-
Ряды Тейлора и Маклорена.
Р ис
1
ис
1
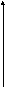


f(b)
 B
B
 A
A

 f(a)
f(a)
 0 а
в х
0 а
в х
28. Интегрирование разложением. Метод подстановки. Интегрирование разложением
 Метод
подстановки
Метод
подстановки
Интегрирование путём введения новой переменной, основанной на формуле
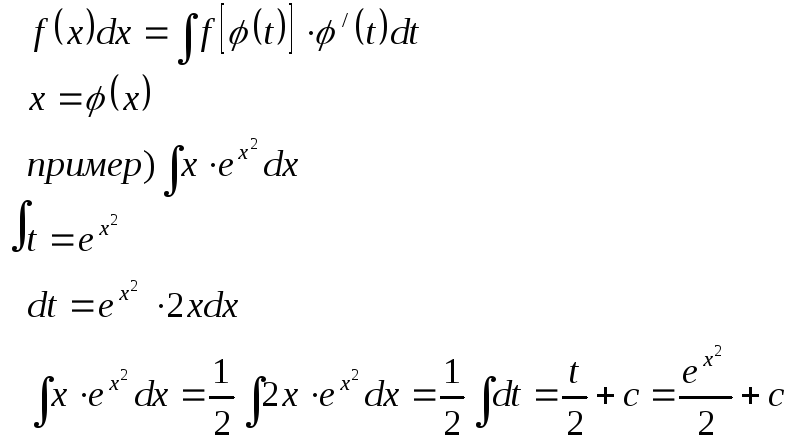
29. Метод интегрирования по частям. Если и=φ1(х), v=φ2(х) – диференциальн. ф-ии, то из формулы диференциала произведения двух ф-ий d(u∙v)/ = udv + vdv получается формула интегрирования по частям
![]()
Эта формула применяется в случае, когда подинтегральная ф-ия представляет собой произведение алгебраической ф-ии и трансцендентной.
В качестве и, обычно, выбирается ф-ия, которая упрощается дифференцированием, а в качестве dv оставшаяся часть подинтнгрального выражения, содержащая dx, из которой можно определить v, путём интегрирования. Пример:
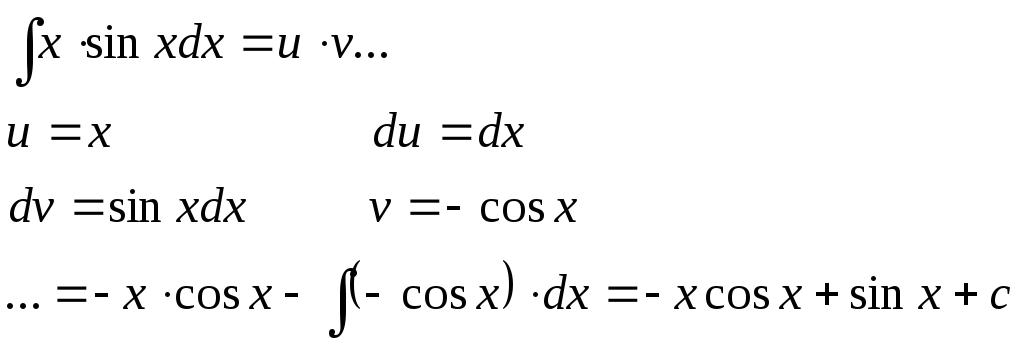
3 0.
Интегрирование некоторых функций,
содержащих квадратный трехчлен.
0.
Интегрирование некоторых функций,
содержащих квадратный трехчлен.