37. Колебания колец Сатурна.

П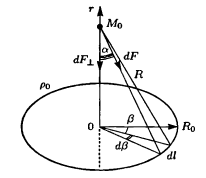остроим модель движения точечной

массы M0 в поле сил тяготения,

создаваемом материальным кольцом с

радиусом R0 и линейной плотностью ро0.

Кольцо считается бесконечно тонким,

движение происходит вдоль оси кольца. Данная схема может рассматриваться как идеализация процесса колебаний колец Сатурна. Несмотря на существенные упрощения, непосредственное использование закона всемирного тяготения

где F — сила притяжения двух тел, имеющих массы m0 и m1, r

расстояние между ними, гамма — постоянная тяготения, не может дать

окончательной модели движения колец Сатурна, так как массы mо, m1

должны быть точечными. Поэтому вычислим сначала силу притяжения между точечной массой Мо и массой dm, содержащейся в малом элементе кольца dl, которую уже можно считать точечной:

Здесь R, г — соответственно расстояние от массы Мо до кольца и

до центра кольца.

Найдем проекцию силы dF на ось r

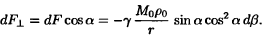
Просуммировав теперь силы тяготения, создаваемые всеми элементами кольца, т. е. взяв интеграл от dF по бетта от 0 до 2PI, найдем результирующую силу.

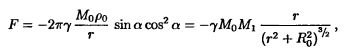
где M1= 2Pi*Ro*po0— полная масса кольца. Горизонтальная проекция результирующей силы равна нулю из-за симметричного расположения кольца относительно массы Мо.

Если r намного больше R0, то данное выражение будет аналогично закону всемирного тяготения. Если же r намного меньше R0, то

Применяем к массе М0 2 закон Ньютона:

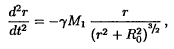- ДУ колебаний

При r значительно меньшем R0 оно становится линейным. Это свободные незатухающие колебания.

Это уравнение однородное линейное. Его характеристическое уравнение имеет вид 

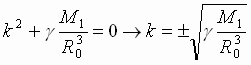
а общее решение запишется в виде

,  .

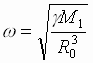38. Движение шарика, присоединенного к пружине.

В задачах динамики можно использовать такую схему: сначала с помощью закона Ньютона связать проекции ускорения тела с проекциями действующих на него сил, а затем, исходя из тех или иных соображений, вычислить эти силы как функции координат (и скорости), получив замкнутую модель. Продемонстрируем этот подход на примере движения шарика, прикрепленного к пружине с жестко закрепленным концом.

Пусть - координата шарика вдоль оси пружины, лежащей на горизонтальной плоскости, и направление движения шарика совпадает с ее осью. И пусть - масса шарика, - длина пружины в ненапряженном состоянии.

Начнем со второго закона Ньютона .

Считаем плоскость идеально гладкой и пренебрегаем сопротивлением воздуха. Вес шарика уравновешен реакцией плоскости. Единственная сила, действующая на шарик в направлении оси – сила упругости пружины. Определим ее, используя закон Гука, гласящий, что для растяжения (сжатия) пружины необходимо приложить силу , где  - характеризует упругие свойства пружины, а  - величину ее растяжения или сжатия относительно нейтрального, ненагруженного состояния.

Уравнение движения шарика принимает вид (линейный осциллятор)

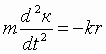Оно описывает свободные незатухающие колебания с собственной частотой 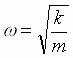и имеет общее решение

Значения и находятся из начальных условий, то есть через величины , . V=dr/dt

Проверим правильность этой модели, основанной на втором законе Ньютона с помощью закона сохранения энергии. Так как точка крепления пружины неподвижна, то стенка не совершает работы над системой "пружина-шарик", и ее полная механическая энергия останется постоянной. Кинетическая энергия определяется движением шарика (пружина невесома) 

.

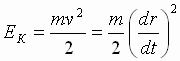Потенциальная энергия содержится в пружине, ее можно найти, определив работу, необходимую для растяжения пружины на величину

.

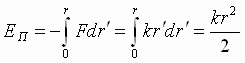Для неизменной со временем величины получаем

.

Так как 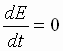, то, продифференцировав интеграл энергии по , приходим к выражению

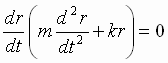То есть получили ту же зависимость, как и из закона Ньтютона.

Даже в простейших ситуациях для построения моделей может потребоваться использование не одного, а нескольких фундаментальных законов.

Прямое формальное применение фундаментальных законов к объекту, рассматриваемому как целое, не всегда возможно. В этих случаях требуется просуммировать элементарные акты взаимодействия между его частями, принимая во внимание свойства объекта.

Одними и теми же моделями могут описываться совершенно разные по своей природе объекты, подчиняющиеся разным фундаментальным законам, и, наоборот, данному закону могут отвечать принципиально разные модели.

Необходимо использовать все возможности для проверки правильного построения моделей (предельные переходы, другие фундаментальные законы).

В задаче о всплытии подводной лодки учесть сопротивление воды, принимая силу сопротивления , где u - вертикальная составляющая скорости лодки. А также найти max глубину, при всплытии с которой можно пренебречь силой , в любой момент времени (должно выполняться требование , )

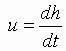По второму закону Ньютона

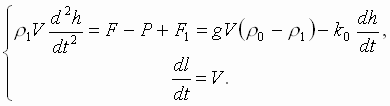
или

.

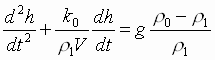Соответствующее характеристическое уравнение имеет вид

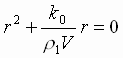..Отсюда , .

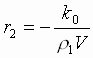Тогда общее решение запишется в виде

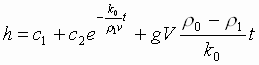, при этом

.

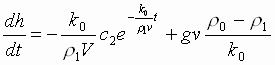Удовлетворим начальным условиям , .

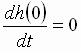Получим , .

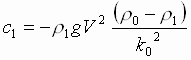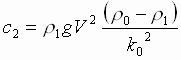В результате можно записать,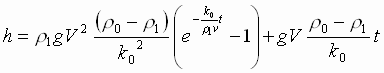

.

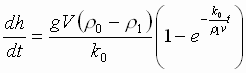Следовательно,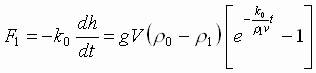

или.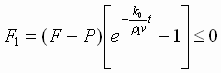

Требуя , получим .

Значит, 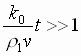, но , тогда .

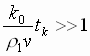Подставляя в неравенство ранее найденное 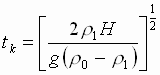, имеем .

Тогда .

Пусть расстояния между точкой нейтрального положения пружины и стенкой, к которой она крепится, равно . Найти условия на величины , при выполнении которых шарик не может удариться о стенку.

Так как , имеем

, , .

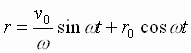Условия максимума:

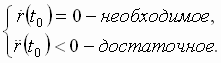
Итак, из условия имеем

, следовательно, ,

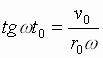из условия имеем.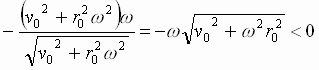

Здесь учтено, что , .

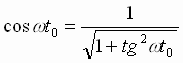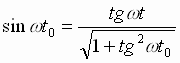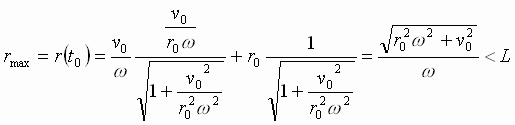
Так как 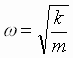, то или .

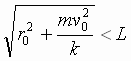Или, возведя в квадрат обе части 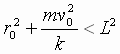, откуда

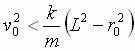
или 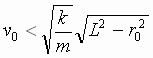при этом .