23.Еквівалентні нескінченно малі функції

Означення

Нескінченно малі функції при х→а α₁(х) і α₂(х) називаються еквівалентними, якщо .

Їх позначають α₁(х) ~ α₂(х), при х→а.

Очевидні такі властивості еквівалентних нескінченно малих функцій, при х→а: 1) α₁(х) ~ α₁(х); 2) якщо α₁(х) ~ α₂(х), то α₂(х) ~ α₁(х); 3) якщо α₁(х) ~ α₂(х), а α₂(х) ~ α₃(х), то α₁(х) ~ α₃(х).

Теорема 1

Нехай нескінченно мала α₁(х) ~ α₁^*(х), при х→а і α₂(х) ~ α₂^*(х), при х→а. Якщо існує границя , то існує границя і ці границі рівні.

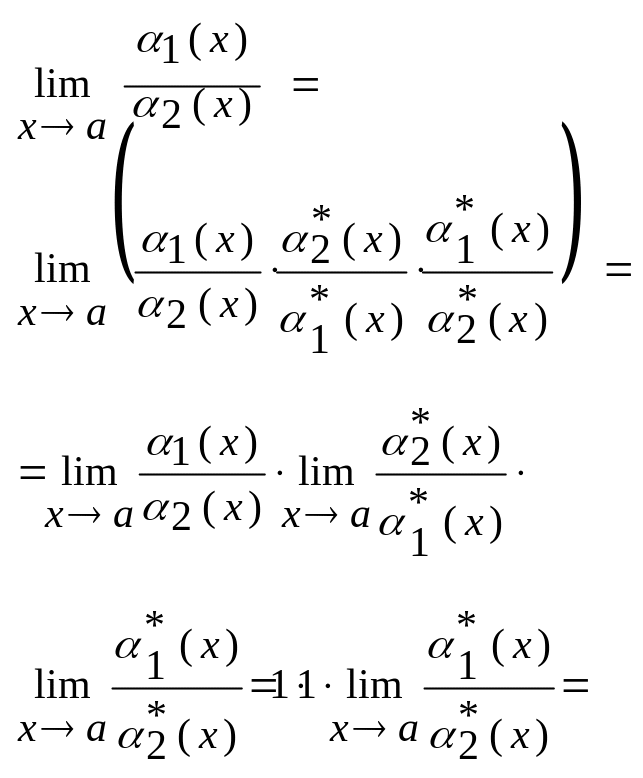
Доведення: розглянемо Теорема 1 дає можливість при знаходженні границі відношення двох нескінченно малих функцій кожну з них (або тільки одну) заміняти еквівалентною нескінченно малою функцією.

Важливі еквівалентні нескінченно малі функції (x→0)

1) sinx~x; 2) tgx~x; 3) arcsinx~x; 4) arctgx~x; 5) 1-cosx~x²/2; 6) e^x-1~x; 7) a^x-1~x·lna; 8) log_a(1+x) ~x·log_ae; 9) ln(1+x) ~x; 10) (1+x)^µ-1~µx.

ї

24.Теореми про еквівалентні нескінченно малі функції

Теорема 2

Нехай α₁(х) і α₂(х) нескінченно малі функції при х→а. Для того, щоб ці функції були еквівалентними необхідно і достатньо, щоб різниця α₁(х) - α₂(х) була нескінченно малою функцією вищого порядку при х→а, ніж кожна з цих функцій.

Доведення: Необхідність: нехай α₁(х) ~ α₂(х). Розглянемо Таким чином (α₁(х) - α₂(х))=о(α₁(х)). Розглянемо також 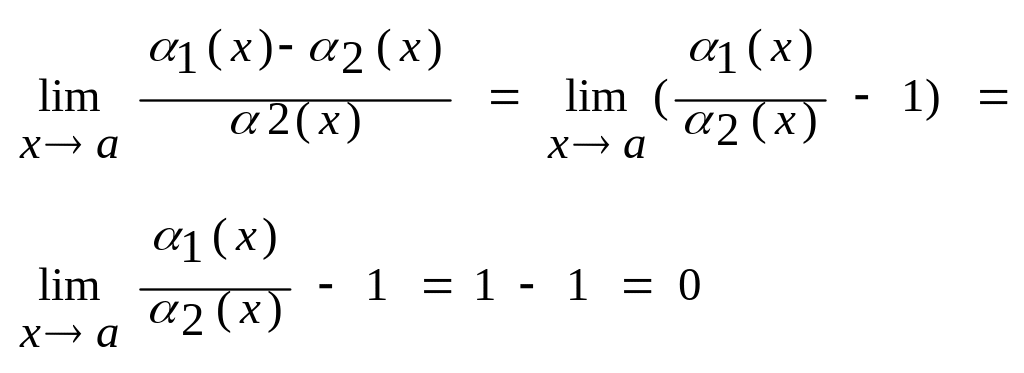Достатність: нехай (α₁(х) - α₂(х))=о(α₁(х)). Тоді α₂(х) ~ α₁(х). Нехай (α₁(х) - α₂(х))=о(α₂(х)). Тоді α₁(х) ~ α₂(х). Теорема доведена.

Теорема 3

Сума нескінченно малих функцій різних порядків еквівалентна доданку нижчого порядку.

Доведення: розглянемо дві функції. У загальному випадку доведення аналогічне. Нехай α₁(х) і α₂(х) нескінченно малі функції при х→а і нехай α₂(х) нескінченно мала функція нижчого порядку, ніж α₁(х). Тобто . Розглянемо . Тоді α₁(х)+α₂(х) ~ α₂(х) при х→а.

25.Неперервність функції в точці

Означення 1

Нехай функція визначена в точці х=а і у деякому околі цієї точки. Функцію називають неперервною в точці а, якщо в цій точці існує границя функції і вона дорівнює значенню функції . Тобто [1].

Зауваження:

1 ) слід відрізняти означення неперервності функції в точці і означення границі функції в точці. При визначенні границі точка а могла і не належати ОВ функції. А якщо точка а і належала ОВ ѓ(х), то в цій точці могли і не співпадати значення функції ѓ(а) з границею . 2) оскільки , то формулу [1] можна записати у вигляді [2]. Формула [2] виражає правило граничного переходу: при знаходженні границі неперервної функції ѓ(х) можна перейти до границі під знаком функції. Геометричний зміст поняття неперервності відповідає геометричному змісту границі [1]. Точки графіка функції як завгодно близьких до точки (а, ѓ(а)), якщо їх абсциса достатньо мало відрізняється від а. Означення 1 можна формулювати і на „мові ε-δ”.

Означення 1’

Функція ѓ(х) називається неперервною в точці а, якщо вона визначена в цій точці і деякому її околі і Коротко це можна записати так: Розглянемо різницю, що входить до нерівності [3] і [4]. Позначимо через ∆х=х-а і назвемо величину ∆х приростом аргументу. Через ∆ѓ= ѓ(х)- ѓ(а)= ѓ(∆х+а)-ѓ(а) і назвемо величину ∆ѓ приростом функції, якій відповідає величина приросту аргументу ∆х. Розглянемо границю [1]. 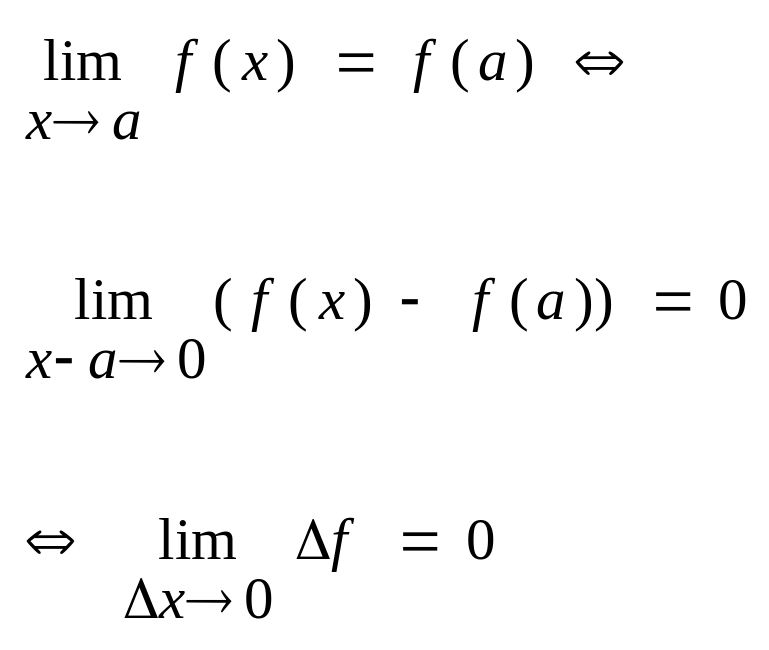Ми одержали третє рівносильне означення неперервності функції в точці.

Означення 1’’

Функція ѓ(х) називається неперервною в точці а, якщо вона визначена в цій точці і у деякому її околі і нескінченно малому приросту аргументу в цій точці відповідає нескінченно малий приріст функції.