
- •1.Основні поняття матем. Логіки. Числові проміжки.
- •2.Множини
- •3.Змінні і сталі величини. Модуль величини.
- •4. Послідовність. Границя послідовності. Границя змінної.
- •5. Єдність границі послідовності. Обмежена і необмежена послідовності.
- •6. Граничниц перехід у нерівностях. Теор. Про границю проміжної послід.
- •7. Нескінченно малі послідовності
- •Необхідність
- •8. Нескінченно великі послідовності
- •9.Арефметичні операції над границями послідовностей
- •10. Монотонні послідовності
- •11.Число е
- •12.Границя за Коші. Геом. Зміст
- •13.Границя функції за Гейне
- •Достатність
- •14.Односторонні границі функції
- •Необхідність
- •15.Арефметичні операції над границями функцій
- •16.Властивість функції, що мають границю
- •17.Граничний перехід у нерівностях для функцій Теорема про границю проміжної функції
- •18.Перша важлива границя
- •19.Друга важлива границя
- •20.Нескінченно великі і нескінченно малі функції
- •21.Основні властивості нескінченно малих функцій
- •Теорема 3
- •23.Еквівалентні нескінченно малі функції
- •24.Теореми про еквівалентні нескінченно малі функції
- •25.Неперервність функції в точці
- •26.Одностороння неперервність функцій в точці. Неперервність функцій на проміжку. Точки розрива функції
- •27.Дії над неперервними функціями. Неперервність складної функції.
- •29.Деякі важливі границі:
- •31.Геометричний зміст похідної, рівняння дотичної.
- •33.Похідні суми, добутку і частки
Достатність
Нехай функція має в точці а границю за Гейне. Припустимо, що в цій точці границя за Коші не існує.
Тобто
![]() ,
це означає що
,
це означає що
![]()
Розглянемо
послідовність
![]() Тоді для кожного числа цієї послідовності
Тоді для кожного числа цієї послідовності
![]()
Перейдемо
у нерівності (3) до границі при
![]() ,
оскільки
,
оскільки
![]() за
теоремою про границю проміжної
послідовності
за
теоремою про границю проміжної
послідовності![]() ,
но з нерівності (4) випливає, що послідовність
,
но з нерівності (4) випливає, що послідовність
![]() не
прямує до А, тобто ми побудували
послідовність, що прямує а для якої
послідовність відповідних значень
функції не прямує до А, це означає, що
функція в точці а не має границі за
Гейне, що суперечить умові теореми.
не
прямує до А, тобто ми побудували
послідовність, що прямує а для якої
послідовність відповідних значень
функції не прямує до А, це означає, що
функція в точці а не має границі за
Гейне, що суперечить умові теореми.
Одержана суперечність доводить
достатність.
14.Односторонні границі функції
Означення 1
Число
![]() ,
називають границею функції
в
точці х=а справа, якщо ця функція визначена
у правому
-
околі точки а.
,
називають границею функції
в
точці х=а справа, якщо ця функція визначена
у правому
-
околі точки а.
Для
будь-якого завгодно малого
![]()
Позначають
це так
![]() або
або
![]()
Означення 2
Число
![]() ,
називають границею функції
в точц х=а зліва, якщо ця функція визначена
у лівому
-
околі точки а, крім можливо самої точки.
,
називають границею функції
в точц х=а зліва, якщо ця функція визначена
у лівому
-
околі точки а, крім можливо самої точки.
Для
будь-якого завгодно малого
![]()
![]()
Запис
![]() ,означає,
що
набуває значень більше від а
,означає,
що
набуває значень більше від а
Запис
![]() ,означає,
що
набуває значень меньших від а
,означає,
що
набуває значень меньших від а
Якщо а=0, то у цьому випадку односторонні границі ліва і права відповідно позначають
![]()
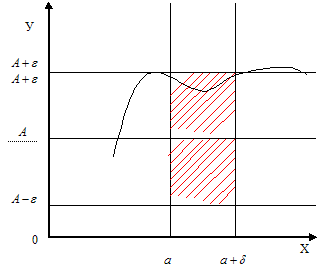

Теорема
Для того щоб функція в очці а мала границю А, необхідно і достатньо, щоб в цій точці існували односторонні границі кожна з яких дорівнювала А.
Доведення
Необхідність
Нехай
в точці а функція
має
границю А
,
за означенням границі для будь-якого
завгодно малого
,
існує
![]()
Нерівність (1) еквівалентна сукупності нерівностей
![]()
![]()
![]()
![]() Достатність
Достатність
Нехай , тоді за означенням
![]()
![]()
![]()
![]()
Тоді, а це означає
Теорема доведена
15.Арефметичні операції над границями функцій
Теорема 1(про границю суми)
Якщо
![]() ,
,![]() ,
де А, В – скінченні числа, то
,
де А, В – скінченні числа, то
![]()
Доведення
Нехай
послідовність
![]()
За означенням границі функції за Гейне.
![]() ,
,![]() ,
тоді за теоремою (про границю суми
послідовностей), границя суми дорівнює
сумі границь, тобто
,
тоді за теоремою (про границю суми
послідовностей), границя суми дорівнює
сумі границь, тобто
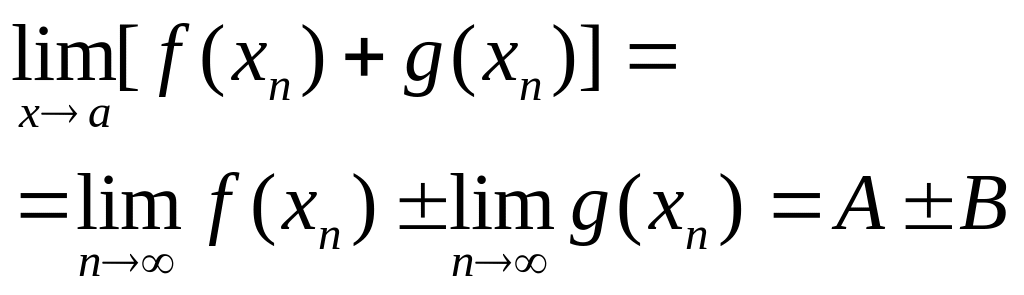
Ця
рівність доведена для будь-якої
послідовності
,
де
![]()
Теорема 2 (про границю добутку):
Якщо
,
,
де А, В – скінченні числа, то
![]()
Доведення
Розглянемо
послідовність
,
тоді за означенням границі функції за
Гейне
![]() ,
,![]()
За теоремою (про границю добутку послідовностей) границя добутку дорівнює добутку границь

Оскільки ця рівність доведена для будь-якої послідовності , то
Теорема 3(про границю частки)
Якщо
,
,
де А, В – скінченні числа
причому![]() то
то
![]()
Доведення
Розглянемо послідовність , тоді за означенням границі функції за Гейне, , , причому
За теоремою (про границю частки послідовностей) границя частки дорівнює частці границь
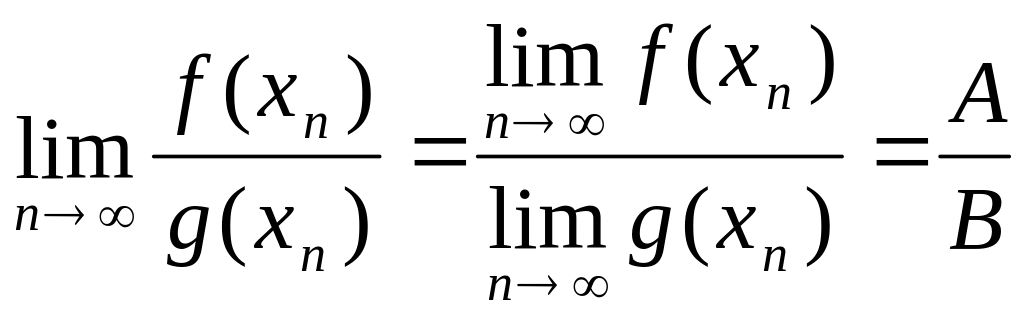
Оскільки ця рівність доведена для будь-якої послідовності , то
16.Властивість функції, що мають границю
Теорема 1(про єдність границі функції)
Якщо функція має в точці х=а границю, то ця границя єдина
Доведення
Припустимо
супротивне
,![]() ,
причому
,
причому
![]()
Розглянемо будь-яку послідовність
Тоді за означенням функції за Гейне одержимо, що послідовність повинна мати дві різні границі А і В але за теоремою про єдність границі послідовності це не можливо. Одержана суперечність доводить теорему.
Теорема 2 (про обмеженістьфункції, що має границю)
Якщо функція має скінченну границю в точці а, то ця функція буде обмеженою у де-якому виколотому околі а.
![]()
Доведення
Нехай
,
за означенням границі функції
![]()
Тоді
![]()
Отримаємо
![]()
Позначимо
через
![]() ,
тоді
,
тоді
![]()
Теорема доведена.
