Экспоненциальное распределение

Определение 6. Непрерывная случайная величина Х, принимающая неотрицательные значения, имеет экспоненциальное распределение с параметром , если плотность распределения имеет следующий вид:

^. (3)

Можно показать, что (сделать самостоятельно).

Функция распределения случайной величины Х равна

, т.е.

. (4)

Если случайная величина Х распределена по экспоненциальному закону, то

P(a  x  b) = F(b) – F(a) = e^-a – e^-b (показать самостоятельно).

Графики плотности и функции распределения приведены на рис. 2.

Рис. 2

Нормальное распределение

Определение 7. Непрерывная случайная величина имеет нормальное распределение, с двумя параметрами a, , если

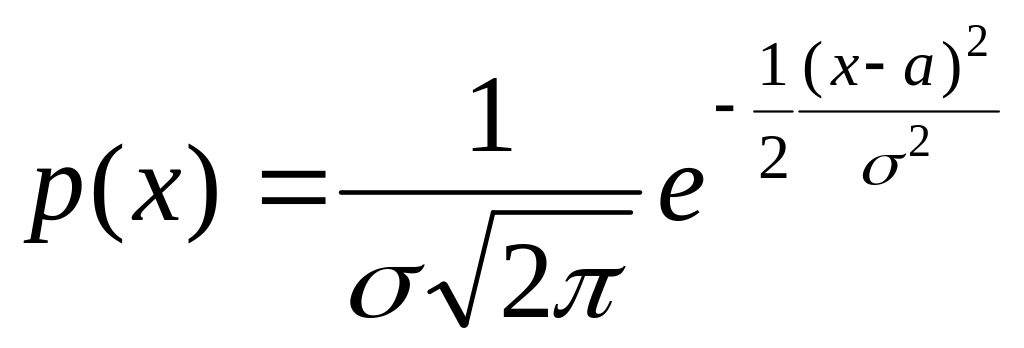, >0. (5)

Тот факт, что случайная величина имеет нормальное распределение, будем кратко записывать в виде Х  N(a;).

Покажем, что p(x) – плотность

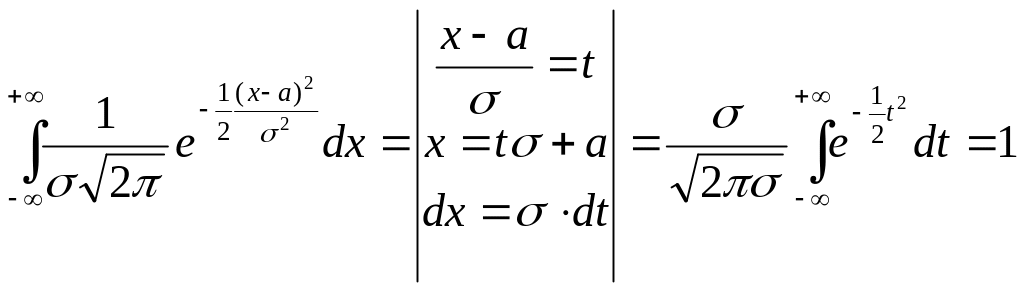(показано в лекции 6).

График плотности нормального распределения (рис. 3) называют нормальной кривой (кривой Гаусса).

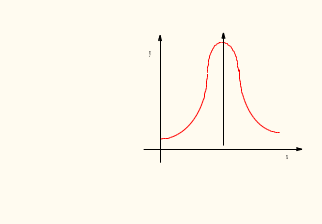
Рис.3

Плотность распределения симметрична относительно прямой х = a. Если х  , то р(х)  0. При уменьшении  график «стягивается» к оси симметрии х = a.

Нормальное распределение играет особую роль в теории вероятностей и ее приложениях. Это связано с тем, что в соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет «примерно» нормальное распределение.

Так как – плотность нормального закона распределения с параметрами а = 0 и  =1, то функция = Ф(х), с помощью которой вычисляется вероятность , является функцией распределения нормального распределения с параметрами а = 0 и  =1.

Функцию распределения случайной величины Х с произвольными параметрами а,  можно выразить через Ф(х) – функцию распределения нормальной случайной величины с параметрами а = 0 и  =1.

Пусть Х  N(a;), тогда

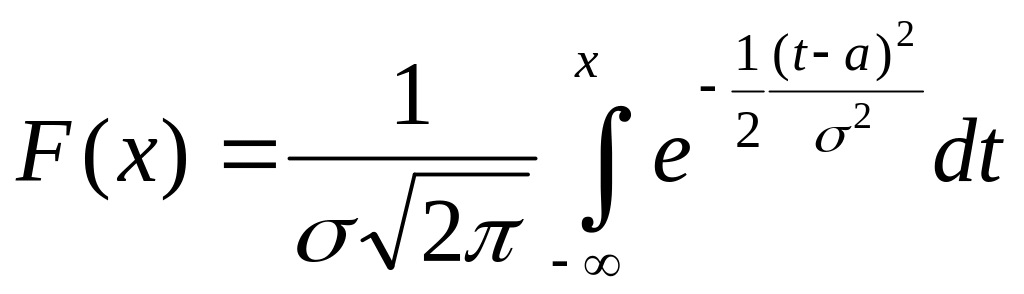. (6)

Сделаем замену переменных под знаком интеграла , получим

=

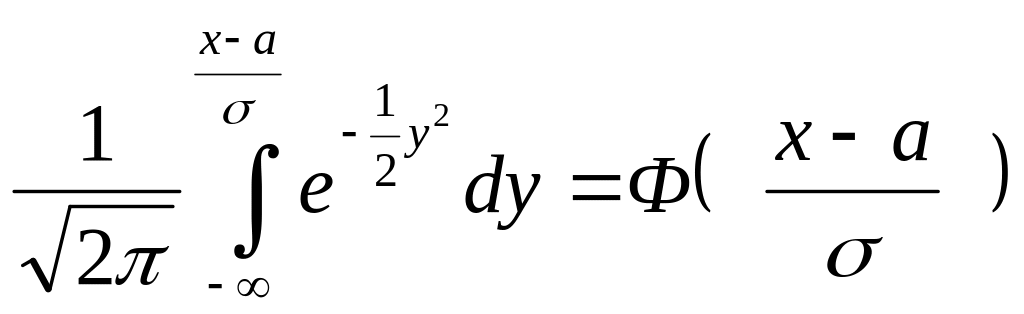
F(x) = . (7)

В практических приложениях теории вероятностей часто требуется найти вероятность того, что случайная величина примет значение из заданного отрезка . В соответствии с формулой (7) эту вероятность можно найти по табличным значениям функции Лапласа

. (8)

Найдем медиану нормальной случайной величины Х  N(a;). Так как плотность распределения р(х) симметрична относительно оси х = а, то

р(х < a) = p(x > a) = 0,5.

Следовательно, медиана нормальной случайной величины совпадает с параметром а:

Х_0,5 = а.

Задача 1. Поезда в метро идут с интервалом в 2 мин. Пассажир выходит на платформу в некоторый момент времени. Время Х, в течение которого ему придется ждать поезд, представляет собой случайную величину, распределенную с равномерной плотностью на участке (0, 2) мин. Найти вероятность того, что пассажиру придется ждать ближайший поезд не более 0,5 мин.

Решение. Очевидно, что p(x) = 1/2. Тогда, Р_0,5 = Р(1,5<X<2) = = 0,25

Задача 2. Волжский автомобильный завод запускает в производство новый двигатель. Предполагается, что средняя длина пробега автомобиля с новым двигателем – 160 тыс. км, со стандартным отклонением – σ = 30 тыс.км. Чему равна вероятность, что до первого ремонта число км. пробега автомобиля будет находиться в пределах от 100 тыс. км. до 180 тыс. км.

Решение. Р(100000< X < 180000) = Ф(2/3)–Ф(–2) = 0,2454 + 0,4772 = 0,7226.