Лекция 24. Проверка гипотезы о равенстве средних

В практических исследованиях часто встречаются случаи, когда средний результат одной серии экспериментов отличается от среднего результата другой серии. При этом правомочен вопрос, можно ли объяснить обнаруженное расхождение средних неизбежными случайными ошибками эксперимента или оно вызвано определенными причинами. В промышленной статистике задача сравнения средних возникает, когда идет речь о контроле или соответствии качества изделий, изготовленных на различном оборудовании или при различных технологических режимах; в медицине – при сравнении эффективности методов лечения; в финансовом анализе – при сравнении уровня доходности ценных бумаг и т.д. Рассмотрим один из вариантов проверки гипотезы о равенстве средних, в предположении, что выборки независимы, признаки имеют нормальное распределение и сравниваются между собой две совокупности. Если одно из этих предположений не выполняется, то применяют непараметрические критерии.

Пусть имеются генеральные совокупности Х и Y, характеризующиеся средними , и известными дисперсиями и . Необходимо проверить гипотезу Н_о о равенстве генеральных средних Н_о: = . С этой целью из этих совокупностей взяты две независимые выборки объемов n₁ и n₂, по которым найдены средние арифметические , и выборочные дисперсии . При достаточно больших n₁ и n₂ и имеют приближенно нормальные законы распределения, соответственно

.

В случае справедливости гипотезы Н_о имеем М( – )=M( ) – M( ) = – = 0. При этом разность – имеет нормальное распределение, а , поэтому при выполнении гипотезы Н_о статистика t имеет нормальное распределение, т.е.

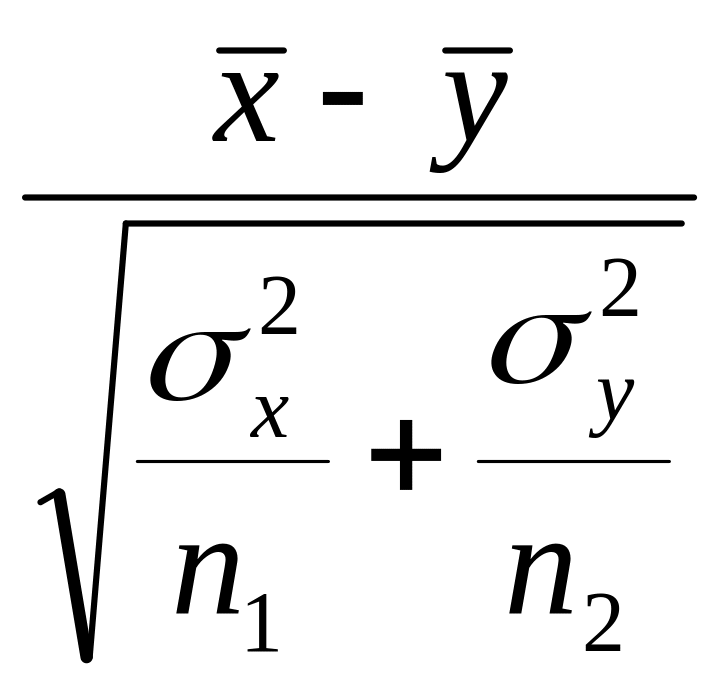
=  N(0,1). (1)

Критическая область критерия выбирается следующим образом:

– если наблюдаемое значение |t|>t_кр , то гипотеза Н_о не принимается;

– если – |t|≤t_кр , то гипотеза Н_о принимается, t_кр определяется из уравнения

Ф(t_кр) = Ф(t_1-) = 1 – ,

где  – уровень значимости критерия, Ф – функция Лапласа.

Если и неизвестны, то используется статистика

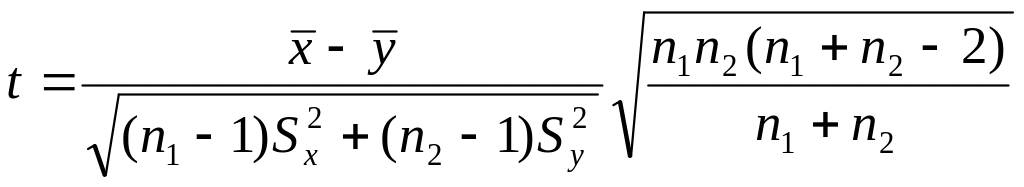. (2)

Известно, что статистика t имеет распределение Стьюдента с k = n₁ + n₂ – 2 степенями свободы. Критическая область устанавливается по следующему правилу: если t>t_,k, то гипотеза Н_о отвергается; в противном случае – принимается, t_,k = t_кр находят из соответствующей таблицы приложений.

Проверка гипотезы о равенстве дисперсий

Необходимость в использовании гипотез о равенстве дисперсий возникает часто, так как дисперсии характеризуют такие показатели, как точность измерительных приборов, технологических процессов, кучность стрельбы, риск экономических или финансовых операций и т.д.

Рассмотрим процедуру сравнения дисперсий в двух совокупностях с нормально распределенными признаками. Пусть дисперсии двух нормально распределенных совокупностей равны и . Необходимо проверить нулевую гипотезу о равенстве дисперсий –

Н_о: = (3)

Для проверки гипотезы (3) из этих совокупностей взяты выборки объема n₁ и n₂, По выборкам посчитаны выборочные дисперсии . В качестве статистики используется величина F = (в числителе ставится бòльшая). Известно, что F имеет распределения Фишера с k₁ = n₁–1, k₂ = n₂ –1 степенями свободы.

Если F > F_кр = F_,k1,k2, то Н_о отвергается, в противном случае гипотеза принимается.

Рассмотрим процедуру сравнения дисперсий нескольких совокупностей с нормально распределенными признаками. Пусть имеется l нормально распределенных совокупностей, дисперсии которых равны соответственно ₁² , ₂²_{, …,}_l² и l независимых выборок из каждой совокупности объемов n₁, n₂, …, n_l. Нулевая гипотеза о равенстве дисперсий имеет вид

Н_о = ₁² = ₂² = _…= _l² = ². (4)

Известно, что если гипотеза Н_о справедлива, то статистика ², вычисленная по формуле (4) имеет распределение Пирсона с l –1 степенями свободы

² = ,

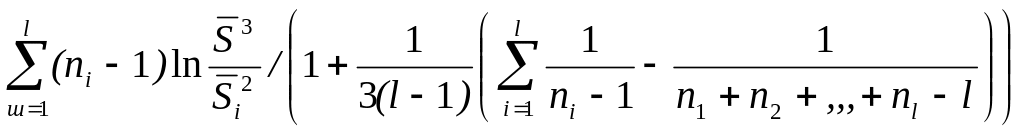где – исправленная выборочная дисперсия l-й выборки;

.

Правило проверки состоятельности нулевой гипотезы следующее: если t > t_,k, то гипотеза Н_о отвергается; в противном случае – принимается, t_,k = t_кр находят из соответствующей таблицы приложений.