Статистическое определение вероятности

Существует большой класс событий, вероятности которых не могут быть вычислены с помощью классического определения. В первую очередь это события с неравновозможными исходами (например, игральная кость «нечестная», монета сплющена и т.д.). В таких случаях может помочь статистическое определение вероятности, основанное на подсчете частоты наступления события в испытаниях.

Определение 2. Статистической вероятностью наступления события А называется относительная частота появления этого события в n произведенных испытаниях [4], т.е.

(А) = W(A) = m/n,

где (А) – статистическое определение вероятности; W(A) – относительная частота; n – количество произведенных испытаний; m – число испытаний, в которых событие А появилось. Заметим, что статистическая вероятность является опытной, экспериментальной характеристикой.

Причем при n → ∞, (А) → P(А), так, например, в опытах Бюффона (XVIII в.) относительная частота появления герба при 4040 подбрасываниях монеты, оказалось 0,5069, в опытах Пирсона (XIX в.) при 23000 подбрасываниях – 0,5005.

Геометрическое определение вероятности

Еще один недостаток классического определения, ограничивающий его применение, является то, что оно предполагает конечное число возможных исходов. В некоторых случаях этот недостаток можно устранить, используя геометрическое определение вероятности. Пусть, например, плоская фигура g составляет часть плоской фигуры G (рис.3).

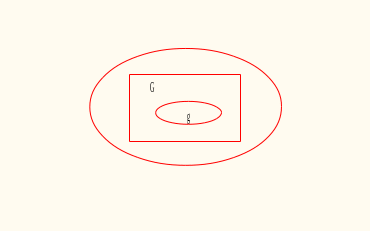
Рис.3

На фигуру G наудачу бросается точка. Это означает, что все точки области G «равноправны», в отношении попадания туда брошенной случайной точки. Полагая, что вероятность события А – попадание брошенной точки на g пропорциональна площади этой фигуры S_g и не зависит ни от ее расположения относительно области G, ни от формы g, найдем

Р(А) = S_g/S_G

где S_G – площадь области G. Но так как области g и G могут быть одномерны- ми, двухмерными, трехмерными и многомерными, то, обозначив меру области через meas, можно дать более общее определение геометрической вероятности

P = measg / measG.

Последовательность испытаний. Формула Бернулли

Рассмотрим следующие примеры.

1. Монета подбрасывается 10 раз. Пусть Х – число появившихся гербов.

2. Известно, что в 80% жителей Краснодара предпочитают добираться на работу личным автотранспортом. Случайно выбрано 7 человек. Пусть Y – число людей в выборке, предпочитающих личный автотранспорт.

3. Известно, что 60% юношей непригодны к службе в армии. Случайным образом отобраны 12 юношей. Пусть Z – число годных к воинской службе юношей.

Что является общим для случайных величин Х, Y, Z. Они являются примерами случайных величин, базирующихся на эксперименте, который называется схемой Бернулли.

Пусть производится последовательность независимых испытаний, в каждом из которых может произойти отдельное событие A – успех или может наступить противоположное событие – неудача. Такая последовательность испытаний называется схемой Бернулли. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность не наступления события А в каждом испытании также постоянна и равна q = 1 – p.

Поставим перед собой задачу вычислить вероятность того, что при n испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится n – k раз. Важно подчеркнуть, что не требуется, чтобы событие повторилось ровно k раз в определенной последовательности.

Вероятность одного сложного события, состоящего в том, что в n испытаниях событие А наступит k раз и не наступит n – k раз, по теореме умножения вероятностей независимых событий равна p^kq^{n - k}. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е. . Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события А в n испытаниях) равна вероятности одного сложного события, умноженного на их число: .

Полученную формулу называют формулой Бернулли.

Задачи:

1. По условиям примера 1 найти вероятность того, что герб появится 6 раз.

2. По условиям примера 2 найти вероятность того, что из 7 случайно выбранных людей 4 предпочитают добираться на работу на личном автотранспорте.

3. По условиям примера 3 найти вероятность того, что из 12 юношей все пригодны к воинской службе, ни один не пригоден, 3 пригодны.

4. 60 % изделий фармацевтической промышленности – контрафактные препараты.

Определить вероятность того, что из 5 купленных в аптеке препаратов 2 – поддельные.