4.3.3.2. Определение параметров эмпирической формулы

После того как вид эмпирической зависимости выбран, решается задача определения найлучших коэффициентов (параметров), которые находятся в этой формуле. Как правило, поиск параметров осуществляется для эмпирической формулы, которая приведена к линейному виду. В основном применяют три метода: метод избранных точек, метод средних и метод найменьших квадратов. Последний метод наиболее точный, но и наиболее громоздкий. Поэтому его используют при обработке исследований, которые требуют установления очень точных значений параметров.

Метод избранных точек.

Пусть эмпирическая формула имеет вид (4.17). Нужно найти значения коэффициентов А и В. Наносим на координатную плоскость исследовательские точки (x_i, y_i), как можно ближе к этим точкам проводим прямую (приблизительная прямая). На этой прямой выбираем две произвольных точки N₁(x₁", y₁") и N₂(x₂", y₂"), не обязательно совпадающие с точками (x_i, y_i) и как можно дальше отдаленные одна от одной. Координаты этих точек подставляем в уравнение (4.17), после чего получаем систему:

y₁"=Ax₁"+B

y₂"=Ax₂"+B

Решая систему, находим A и B.

Метод средних

Пусть эмпирическая формула имеет вид (4.17). Подставляем в эту формулу вместо X и Y исследовательские значения x и y. Так как левая часть формулы, как правило, не сравнивается с правой, получаем систему уравнений:

Аx1+B-y1=1; Ax2+B-y2=2; ........................... Axn+B-yn=n.

(4.18)

где ₁, ₂,..., _n - несогласования (отклонения), которые могут быть как положительными, так и отрицательными. Согласно методу средних, наилучшей эмпирической зависимостью принимается та, которая обеспечивает нулевое значение суммы отклонений по все экспериментальным точкам, то есть алгебраическая сумма несогласований равняется нулю

. (4.19)

Определение параметров A и B формулы (4.17) выполняют следующим образом:

1. Составляют условные уравнения y_i=Ax_i +B, число которых равняется числу собственных значений x_і и y_і.

2. Условные уравнения разделяют на приблизительно равные группы, число которых n равняется числу определяемых коэффициентов (в данном случае - 2).

3. Уравнения, которые входят в любую из этих групп, складываются. Для данного случая получаем два уравнения:

(4.20)

4. Из этих уравнений находят неизвестные коэффициенты A и B.

Группирование условных уравнений перед их суммированием можно провести разными способами, причем каждый из них даст несколько разных значений коэффициентов. Рекомендуется группировать уравнения по порядку.

Метод найменьших квадратов.

Эмпирическая формула в общем виде может быть записана так:

Y=F(x_i, A_j) ,

где x_i - независимые переменные; A_j - коэффициенты эмпирической зависимости.

В соответствии с методом найменьших квадратов наилучшими коэффициентами в смысле приближения к экспериментальным данным (y_i=f(x_i)), будут коэффициенты, отысканные с

, (4.21)

то есть минимумом суммы квадратов отклонений между экспериментальными и расчетными значениями.

При фиксированных значениях x функция R(A_j) есть положительно определенной (заданной и неперерывной в интервале [x₁, x_n]).

Пусть эмпирическая формула имеет вид:

F(x_i, A_j) = a₀+a₁.x_i+a₂.x_i²+...+a_m.x_i^m

Тогда выражение (4.21) можно записать так:

(4.22)

Н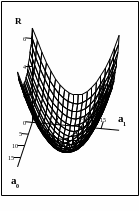 езависимыми переменными для квадратичного функционала R(A_j) являются коэффициенты а₀….а_m. Минимума функционал достигнет в точке, где его частные производные по а₀….а_m будут равны 0. Действительно, зависимость R(A_j) описывается положительно определенной квадратичной параболой, имеющий экстремальную точку (в которой производная =0) – минимум. Например, при использовании в выражении (4.22) только коэффициентов а₀ и а₁ (в этом случае аппроксимирующей зависимостью будет прямая линия) функционал R(A_j) представляет собой параболоид вращения

Найдем частные производные функции R(a₀, a₁,...,a_m) по a₀, a₁,...,a_m и приравняем их к нулю. Получим так называемую нормальную систему m+1 уравнений с m+1 неизвестными a₀, a₁,...,a_m:

(4.23)

Решив систему известными методами (формулы Крамера, метод Гаусса и прочие), найдем коэффициенты a₀, a₁,..., a_m формулы (4.22), которая будет иметь найменьшее квадратичное отклонение R(A_j). На практике, как правило, при определении коэффициентов с использованием метода найменьших квадратов любую эмпирическую зависимость целесообразно привести к линейному виду. Рассмотрим получение системы нормальных уравнений для этого случая. Нужно определить коэффициенты эмпирической формулы:

F(xi, Aj)=a0+a1xi

(4.24)

Тогда выражение (4.22) будет иметь вид:

(4.25)

Нормальная система для определения a₀ и a₁ будет иметь такой вид:

Сделав простые преобразования, имеем:

(4.26)

Решив систему (4.26), получим значения a₀ и a₁. Подставим их в формулу (4.24), и получим конкретный вид эмпирической формулы.

Для аппроксимации квадратичной параболой эмпирическая формула имеет вид:

F(x_i, A_j) = a₀+a₁.x_i+a₂.x_i².

Квадратичный функционал:

Частные производные:

Преобразуем полученную систему уравнений:

.

Преобразованная система – система линейных алгебраических уравнений, решить которую можно методом Гаусса.