4.4. Методы численного интегрирования

Численное интегрирование - это вычисления определенного интеграла по ряду численных значений подынтегральной функции:

(4.27)

при условии, что a и b – конечные, и f(x) является непрерывной функцией x на всем интервале a<=x<=b. Общий подход к решению задачи такой:

Определенный интеграл I представляет собой площадь, ограниченную кривой f(x), осью Х и ординатами в точках x=a и x=b.

Мы будем вычислять I, разбивая интервал от a до b на множество меньших интервалов, находить приблизительную площадь каждой "полосы", получающейся при такой разбивке и суммировать площади этих полос.

Чем меньше интервал разбивки, тем точнее будет вычислена интервальная сумма. При этом значительно увеличится количество вычислений. Поэтому на практике приходится ограничиваться конечной разбивкой интервала интегрирования функции, допуская при этом некоторую ошибку.

Разнообразие методов численного интегрирования обусловлено стратегией выбора точек разбивки, что обеспечивает в каждом конкретном случае минимально возможную ошибку. Возможны два способа выбора точек разбивки исходного интервала. Первый способ - число интервалов фиксируют заранее, второй - число и размеры интервалов определяются в процессе вычисления, исходя из требований заданной точности. В обоих случаях исходная функция на каждом интервале аппроксимируется зависимостью, например, линейной или квадратичной.

Численное интегрирование выполняют по квадратурным формулам:

.

Коэффициенты а_k и абсциссы х_k можно получить разыми способами:

1. По формулам Ньютона-Котеса (формулы точны для многочленов степени  n).

2. По формулам Гаусса (формулы точны для многочленов степени  2n-1, то есть обеспечивают более высокую точность для функций, имеющих производные высоких порядков).

3. Для функции с кусочно-непрерывной 1-й производной лучше применять метод трапеций (частный случай формул Ньютона-Котеса)

4. По обобщениям формул Гаусса, точным для тригонометрических и специальных функций.

Повторное применение методов численного интегрирования позволяет находить кратные (двойные, тройные) интегралы.

Квадратурные формулы Ньютона-Котеса основаны на аппроксимации:

,

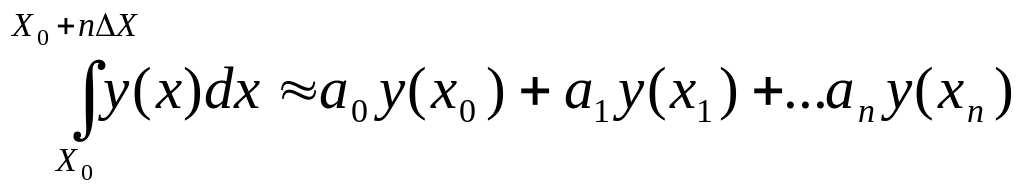где

,

y(x_k) – значения функции для n+1 равноотстоящих значений x_k=x₀+kx (k=0…n). (Число ноль-факториал 0! равно 1).

Формула Ньютона-Котеса является точной, если y(x) – многочлен степени  n.

Частными случаями формулы Ньютона-Котеса являются:

Формула
1. Правило трапеций (n=1)	1/2*X*(Y0+Y1)
2. Правило Симпсона (n=2)	1/3*X*(Y0+4Y1+Y2)
3. Правило Уэддля (n=6)	3/10*X*(Y0+5Y1+Y2+6Y3+Y4+5Y5+5Y6)

4.4.1. Метод трапеций

Метод трапеций основан на том, что график подынтегральной функции на каждом отрезке разбивки заменяется стягивающей его хордой, и площадь, ограниченная интервалом разбивки [X_i-1; X_i] заменяется площадью трапеции:

, (4.28)

где правая часть есть площадью трапеции (см. рис.4.16).

Получим формулу (4.28), подставив в качестве подинтегральной функции уравнение прямой:

Для двух точек прямой справедливо:

, откуда .

Подставив значения коэффициентов а и b в выражение для интеграла, получим уравнение (4.28).

Если: (X_i-X_i-1)=(b-a)/n=h, тогда для определенного интеграла применимо следующее приблизительное значение:

Рис.4.16

, (4.29)

или:

, где h=(b-a)/n. (4.30)

Формула (4.30) называется формулой трапеции для численного интегрирования. Для пользования ею необходимо знать значения подынтегральной функции в точках Хо;Х₁;Х₂...Х_n.

Если подынтегральная функция задана графически, тогда эти значения считываются с графика, а если она задается аналитически, тогда f(Xo),f(X1),...f(Xn) находятся путем подстановки в подынтегральную функцию абсцисс Хо,Х1...Хn.

Б лок-схема метода приведена на рис.4.17.